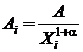УДК 621.31

 

Техноценозы, золотое сечение и логарифм Фибоначчи в системах электроснабжения.

 

Южанников Александр Юрьевич,

кандидат технических наук, профессор,

Южанников Михаил Юрьевич,

аспирант,

кафедра «Электроснабжение и электрический транспорт»

Политехнического института Сибирского Федерального Университета,

г. Красноярск.

 

Электролаборатория

электролаборатория. Низкие цены! Звоните сейчас

electrozamer.ooo

По мере роста и усложнения  промышленных предприятий актуальными становятся проблемы их построения и обеспечения функционирования. Решение этих проблем  основывается на объективных законах, отражающих закономерности развития природы. Законы развития техники, включающей отдельные элементы, и живой природы, состоящей из отдельных особей, имеют много общего. Поэтому представляется возможным описывать сложные технические системы  на основе ценологических понятий [1].

Современное  промышленное предприятие имеет в своем составе сложные технологические, теплотехнические, электрические, телефонные и другие сети. Это комплексное хозяйство является системой нового типа, где свойства системы не вытекают из совокупности свойств ее отдельных элементов. Подобные системы такой сложности рассматриваются в других направлениях науки как ценозы (биогеоценозы, техноценозы, бизнесценозы, ценозы в социальной сфере  и т.д.).

Например, электрическое хозяйство крупного предприятия можно охарактеризовать следующими цифрами: максимум нагрузки достигает сотен МВт, количество установленных двигателей - десятки тыс. шт., сотни силовых трансформаторов, тысячи низковольтных аппаратов, десятки тысяч километров проводов и кабелей.

Известно, что в 1877 г. при исследовании свойств отдельных особей и совокупностей живых организмов Клаус Фердинанд Мебиус ввел понятие «биоценоз». Биоценоз – совокупность живых организмов, обитающих на определенном участке, где условия внешней среды определяют его видовой состав.

Термин  «техноценоз»  и  ценологический подход к исследованию сложных технических систем  предложены  в 1974 г. замечательным ученым  Б. И. Кудриным,  где  техноценоз  определяется как сообщество всех изделий, включающее все популяции;  ограниченное в пространстве и времени; имеющее слабые связи и слабые взаимодействия элементов (изделий), образующих систему  искусственного происхождения, которая характеризуется несопоставимостью времени жизни ценоза и особи, невозможностью выделения однозначной системы показателей.

Кудрин Б.И. предложил использовать модель H-распределения для математического описания видового и рангового распределения

 

где	Аi	-	теоретическое значение числа видов для всех i,
	Xi	-	численность популяции i,
	А,a	-	постоянные видового распределения.

Устойчивость системы  обусловлена действием законов энергетического и информационного отборов по аналогии с живыми системами, где действует закон естественного отбора (табл.1).

 

Таблица 1.

Основные термины описания параллелизма био- и техноэволюции.

Определение	Наименование
	биологическое	технологическое
Самостоятельно функционирующая единица    Элементарная единица эволюции, группа особей одного вида организмов, занимающая область пространства с определенными границами Ограниченное в пространстве и времени любое единство, включающее все популяции (все организмы (изделия)) Сообщество и неживая среда (физико-химические факторы), функционирующие совместно и рассматриваемые как единое; взаимосвязанный комплекс организмов, характерных для известных геофизических условий Направленное постепенное и закономерное изменение популяций в ряду поколений Материальный объект, содержащий закрепленную информацию и предназначенный для ее передачи и использования Устройство изделия, генетическая конституция, записанная с помощью символов; совокупность всех генов (документов), определяющая организм (изделие) Внешнее видимое проявление наследуемых признаков, реализованный комплекс признаков организма Возможность и способность к воспроизведению своего вида Внезапное наследственное изменение, любое изменение, внесенное в документ, по которому изготавливается изделие Формирование экосистем количественно увеличивающимися видами так, что каждое из большинства видов представлено малым числом особей; по мере увеличения количества особей одного вида – число этих видов сокращается	Организм Особь Вид  популяция      биоценоз, биотическое сообщество      биогеоценоз (геобиоценоз), экосистема                   эволюция       ген          генотип       фенотип   размножение       мутация           видовое разнообразие	Изделие Особь Вид (типоразмер)  популяция      техноценоз        экосистема                     техноэволюция       документ          генотип       фенотип   изготовление       вариофикация           ассортица

 

Применительно к промышленным предприятиям определяют, например,  связь между количеством видов продукции и электропотреблением.

 

где		-	электропотребление особи с рангом r,
	W1	-	электропотребление особи с рангом r = 1 (максимальное электропотребление);
	r	-	ранг,
	b	-	ранговый коэффициент, характеризующий форму кривой распределения.

Для рангового распределения показатель b меняется в пределах . На основе зависимости годового электропотребления от разнообразия и структуры выпускаемой продукции прогнозируют параметры электропотребления, опираясь на объем выпускаемой продукции.

Отмеченные ценологические свойства промышленных предприятий констатируют устойчивость явления, проявляющегося с определенного уровня организации некоторого множества элементов с неопределенными связями: способность ценозов формировать в процессе образования и сохранять в процессе развития устойчивую структуру при наличии различных механизмов отбора. Данная теория предполагает существование некоторого идеального распределения элементов ценоза, причем стабильность системы характеризуется значением рангового коэффициента, находящегося в пределах от 0,5 до 1,5.

В работах В.И. Гнатюка предполагается, что оптимальным является такой техноценоз, который по своим функциональным показателям характеризуется максимальной энтропией и обеспечивает выполнение поставленных задач, т.е. идеальное выполнение своего функционального назначения [2].

Функциональное выполнение своего назначения и понятие «идеальная техническая система» уже нашли свое применение в электроэнергетике [3].

Объясним существование идеальной технической системы с точки зрения гармонии и золотого сечения. Предположим, что гармония и идеальное распределение видов  ценоза как системы, выполняющей свое функциональное назначение, подчиняются золотому сечению, а понятие золотое сечение неразрывно связано с числами Фибоначчи.

Считается, что деление отрезка в среднем и крайнем отношении впервые было осуществлено 2500 лет назад Пифагором - великим философом и геометром древней Греции. Он показал, что отрезок единичной длины AB можно разделить точкой  С  на две части так, что отношение большей части (CB=x) к меньшей (AC=1-x) будет равняться отношению всего отрезка (AB=1) к большей части (CB): CB/AC=(AC+CB)/CB, или x/(1-x)=1/x. Отсюда следует алгебраическое выражение x² + x – 1 = 0. Положительным корнем этого уравнения является (-1+√5)/2, так что отношения в рассматриваемой пропорции равны: 1/x = 1,61803...  Число 1,618 обозначается буквой Ф в честь древнегреческого скульптора Фидия. Единичный отрезок  АВ ( 0,382 + 0,618 = 1) делится точкой   С   в соответствии с  пропорцией

 

1 : 0,618 = 0,618 : 0,382 = 1,618.

 

Такое отношение принято называть золотой пропорцией, а соответствующее деление отрезка - золотым делением. Имеются факты, которые говорят о том, что о золотой пропорции знали задолго до Пифагора. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. На принципах золотого деления в древности построено много архитектурных сооружений.  Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

 Французский архитектор Ле Kорбюзье нашел, что в рельефе из храма фараонa Cети I в Абидосе и в рельефе, изображающем фараона Pамзеса, пропорции фигур соответствуют величинам золотого деления. Шмелев И.П. в своей работе «Основы гармонии в искусстве Древнего Египта» провел анализ резных панелей усыпальницы Хеси-Ра и показал методологию золотой пропорции. И. Ш. Шевелев установил, что сановник Хеси - Ра, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

 Платон (427...347 гг. до н.э.) знал о золотом делении. Его диалог "Тимей" посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.  Платон приводит определение гармонического деления – одно из древнейших, дошедших до наших дней. «Для соединения двух частей с третьей совершенным образом необходима пропорция, которая бы скрепила их в единое целое. При этом одна часть целого должна относиться к другой, как целое к большей части».

В 1202 г. вышло в свет сочинение "Liber abacci" итальянского купца и  математика Леонардо Пизанского (предположительно 1180-1240 г.г.), известного как Фибоначчи. Часть этого трактата составляла задача про кроликов, которая гласила: «Сколько пар кроликов рождается в год от одной пары кроликов? И сколько пар кроликов родится в течение года, если через месяц пара кроликов производит на свет другую пару, а рожают кролики со второго месяца своего рождения?».

Решая эту задачу, Фибоначчи получил следующий результат: первая пара в первом месяце дает удвоенное потомство и в этом месяце окажется 2 пары. Из них одна пара (первая пара) рожает и в следующий месяц. То есть во втором месяце получается 3 пары; из них в следующем месяце уже две пары дают потомство, рождается 2 пары и число пар становится 5; и.т.д. Так Фибоначчи обнаружил последовательность чисел, где последующее число равно сумме двух предыдущих чисел:  1; 1; 2; 3; 5; 8; 13; 21; 34, 55, и т.д., эта последовательность  получила название ряда  Фибоначчи. Очевидно,  что начиная с нуля последовательность чисел Фибоначчи можно представить формулой

f_n+2 = f_n +f_n+1,

где n - порядковый номер числа Фибоначчи.

Леонардо да Винчи производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и звучит до сих пор как самое популярное. «Золотое сечение – деление отрезка на две части, при котором длина отрезка так относится к большей части, как большая часть относится к меньшей».

            Великий астроном XVI в. Иоган Kеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение). Кеплер называл золотую пропорцию продолжающей саму себя. «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности» [4].

Интерес к золотому сечению сохраняется и в наши дни. В нашу задачу входит показать значение золотого сечения и чисел Фибоначчи в  сфере  организации  технических систем по аналогии с живой природой. Если взять числовой ряд 1,0;  0,62;  0,38;  0,24;  0,15;  0,09  и т.д. (что напоминает шкалу мощностей трансформаторов), состоящий из чисел с коэффициентом  1,618 («Золотое сечение») и аппроксимировать этот ряд чисел, то получим кривую (рис.1), которая описывается следующей формулой [5]:

 

Фi = Ф0(1-r) где  Фi , Ф0 - текущее и начальное значение чисел, r – ранг числа.

 

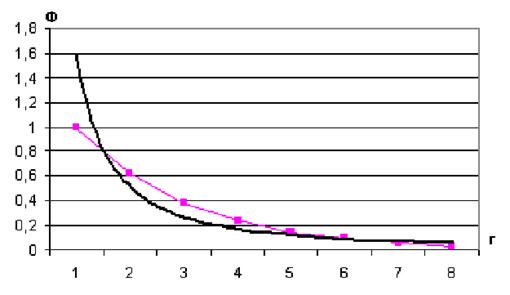
Рис.1.

Числовой ряд и аппроксимационная кривая.

 

Этим числовым рядом  (H-распределение)  можно описывать при ранжировании в ценозе соотношение количества видов и численности каждого вида.

H-распределение можно также аппроксимировать логарифмической зависимостью. Напомним, логарифмом числа N по основанию а (обозначается log_a N) называется показатель степени b, в которую надо возвести число а, чтобы получить число N, т. е., b = log_aN, если а^b = N. Широкое применение нашли логарифмы по основаниям e (число Эйлера) — натуральные логарифмы (ln N) и по основанию 10 — десятичные логарифмы (lg N), а также двоичные логарифмы (log₂N), которые применяются в теории информации. Возьмем основанием логарифма число Ф=1,618, введем понятие «логарифм Фибоначчи» и обозначим логарифм Фибоначчи символом  lF N = log_Ф N.  Данная зависимость позволяет точно описывать исследуемый числовой ряд.

Несмотря на то, что интерес к проблеме Золотого Сечения в настоящее время по-прежнему нарастает, тем не менее, пока еще не создана теория Золотого Сечения в той постановке, которая воспринимается официальной наукой. Пропорции Золотого Сечения должны быть решением некоторой оптимизационной задачи, где присутствует критерий оптимизации, который обычно минимизируется. Пока такая задача для Золотого Сечения еще не сформулирована.

На последние 10-15 лет приходится настоящий бурный всплеск исследований  по проблеме золотого сечения. В эти годы в России и странах СНГ появились крупные работы в различных направлениях науки, где золотая пропорция  и  ее  закономерности использованы как своеобразный методологический принцип, лежащий в основе анализа самоорганизующихся природных и технических систем, их структурной гармонии. 

В работах  А. П. Стахова,  Э. М. Сороко,  Ю. А. Урманцева,  К. Б. Бутусова, М. А. Марутаева,  О. Я. Боднара,  В. Д. Цветкова,  В. В. Очинского,      В. И. Коробко, С. А. Ясинского и многих других  ученых  представлено множество проявлений закономерностей золотого сечения и чисел Фибоначчи  в пропорциях человека, биологии, ботаники, эргономике, архитектуре, поэзии, музыке и т.д.; на многочисленных примерах из различных областей знаний показано, что свойства и закономерности   золотого  сечения и чисел Фибоначчи проявляются в виде принципов оптимальности в организации и функционировании различных систем.

Применение этих закономерностей для поиска оптимальных параметров функционирования  систем  служит одним из приемов, используемых в качестве методологической основы ценологических исследований технических систем.

Эта особенность является проявлением свойств систем ценологического типа, исследованных, в частности Кудриным Б.И. на примере многономенклатурных предприятий химической промышленности. Представляется возможным применение данного подхода для оценки количества и видового разнообразия электротехнического оборудования при проектировании, а в эксплуатации – при прогнозировании электропотребления, электроремонтов и оценке потенциала энергосбережения (сравнивая фактическое и идеальное H-распределение).

 

Вывод.

 

С учетом опыта развития живой природы, можно предполагать, что кривая на    рис. 1 отражает идеальное соотношение количества видов и численности каждого вида в технических системах. Поэтому при определении основных показателей и количества установленного оборудования целесообразно использовать числа Фибоначчи и понятие «золотое сечение». Поскольку эти соотношения существуют в природе, то человек неосознанно создает техноценозы таким образом, что их оптимальная структура определяется этими постоянными.

 

Литература.

 

1.      Кудрин Б.И. Введение в технетику. 2-е изд. переработ. и доп. Томск: Изд-во         Томск .  гос. ун-та, 1993. 552 с.

2.      Гнатюк В.И.  Закон оптимального построения техноценозов. Калининград: КВИ             ФПС РФ – ЗНЦ НТ РАЕН, 2003.- 132 С.

3.      Южанников А.Ю.  Полезность и плата за полезность при выборе компенсирующих устройств. Межвуз. сб. науч. трудов НЭТИ. Новосибирск: НЭТИ,     1990.   С.42-45.

4.      Коробко В.И., Коробко Г.Н. Золотая пропорция и человек. М.  Изд – во  междунар. ассоциации строит. вузов: 2002.-394 с.

5.      Южанников А.Ю. Ценологическая модель и логарифм Фибоначчи в системах электроснабжения // «Академия тринитаризма», М., Эл. № 77-6567,  публ. 14111, 28.12.2006г.

 

Поступила в редакцию 14 октября 2007 г.