УДК 532.5
Связь уравнений плоскопараллельной
фильтрации с системой Карлемана.
Толпаев
Владимир Александрович,
доктор физико-математических наук,
профессор,
зав. кафедрой Прикладной математики и
компьютерных технологий Северо-Кавказского Государственного Технического Университета.
Колесников
Алексей Владимирович,
аспирант, инженер кафедры Прикладной
математики и компьютерных технологий Северо-Кавказского Государственного Технического
Университета.
Введение.
Установившаяся
плоскопараллельная фильтрация несжимаемой жидкости в изотропном неоднородном
пласте с проницаемостью 
, где 
- размерная
постоянная, а 
- безразмерная функция
декартовых координат 
, 
в плоскости течения, описывается
системой уравнений [1]
; 
. (1)
В (1) через 
и 
обозначены потенциал 
и функция тока течения
(где Р – приведенное давление, а 
- динамическая
вязкость жидкости).
Связь уравнений движения жидкости с системой Карлемана.
Многие авторы (О. В. Голубева, Г. В. Голубев, Ю.А. Гладышев, и др.) для решения уравнений
(2)
и
(3)
получающихся в результате перекрестного дифференцирования системы (1), применяли подстановки
и 
. (4)
С помощью подстановок (4) относительно новых вспомогательных функций вместо (2) и (3) получаются уравнения Гельмгольца. Однако целесообразнее применять подстановки (4) не к разрозненным друг от друга уравнениям (2) и (3), а к исходной системе уравнений (1), так как последняя полнее описывает движение жидкости, нежели отдельно одно уравнение (2) или (3).
После подстановки (4) в систему (1), последняя, как легко проверить, примет вид:
(5)
где через 
обозначена функция
. (6)
Система уравнений (5) относится к системе уравнений Карлемана [2]. Практическая польза перехода от системы (1) к системе (5) определяется двумя факторами. Во-первых, для случаев, когда (6) является функцией одной переменной, удается модифицировать метод Н.И.Назарова, позволяющий общее решение системы (5) выразить через произвольную аналитическую функцию комплексного переменного. Заметим, что в этих случаях общее решение системы (1) по методу Н.И. Назарова тоже выражается через произвольную аналитическую функцию, но с более сложными коэффициентами в соответствующих функциональных рядах. Во-вторых, практическая польза перехода к системе (5) определяется еще и тем, что для системы Карлемана, в отличие от системы (1), могут быть предложены итерационные методы решения, что позволит решать задачи фильтрации с помощью новых подходов.
Вывод уравнений для функций 
и 
, удовлетворяющих системе Карлемана.
Дифференцируя
первое уравнение системы (5) по , второе – по и складывая, получим:
,(7)
где 
- оператор Лапласа.
Если умножить первое уравнение системы (5) на 
, второе – на 
и сложить, получим:
, (8)
где 
- оператор «набла», 
, а 
и 
- орты декартовой
системы координат. Теперь, с учетом равенства (8), уравнению (7) можно придать
вид
. (9)
Если в
выражение 
подставить (6), то
после тождественных преобразований окончательно получим следующее уравнение для 
:
, (10)
где
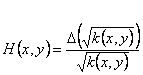. (11)
С помощью аналогичных выкладок для
второй функции 
системы (5) получаем
уравнение
, (12)
где
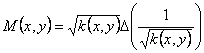. (13)
Эти же самые уравнения (10 и (12) получаются и в результате подстановки (4) в уравнения (2) и (3). Именно так и поступали О.В. Голубева и др. авторы, применявшие в своих решениях подстановки (4). Однако никто из этих авторов не указывал, что решения уравнений (10) и (12), описывающие одно и то же течение, сопряжены друг с другом при помощи системы уравнений Карлемана (5).
Литература.
1) Голубева О. В. Курс механики сплошных сред. – М.: «Высшая школа», 1972.- 368с.
2) Положий Г. Н. Теория и применение 
- аналитических и 
- аналитических
функций и их приложения. – Киев, «Наукова дума»,
1973.- 423с.
Поступила в редакцию 11 января