Исследование гидродинамической
устойчивости расплава при выращивании кристаллов методом Чохральского.
Гаража
Евгения Васильевна,
аспирант Кубанского Государственного Университета,
г. Краснодар.
Научный руководитель – доктор
физико-математических наук, доцент
Тумаев Евгений Николаевич.
В работе [1]
отмечено, что при выращивании монокристаллов методом Чохральского
расплав является конвективно-устойчивым, т.е. в расплаве без подпитки
отсутствуют вертикальные потоки массы, обусловленные осевым градиентом температуры.
Условие конвективной устойчивости авторами работы [1] в согласии с [2]
формулируется в виде
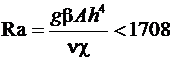 , (1)
, (1)
где ![]() – число Рэлея,
– число Рэлея, ![]() м/с2,
м/с2,
![]() – коэффициент
объемного расширения расплава,
– коэффициент
объемного расширения расплава, ![]() – осевой градиент
температуры в расплаве,
– осевой градиент
температуры в расплаве, ![]() – высота расплава в
тигле,
– высота расплава в
тигле, ![]() и
и ![]() – кинематическая вязкость и температуропроводность
расплава,
– кинематическая вязкость и температуропроводность
расплава, ![]() – теплопроводность,
– теплопроводность, ![]() ,
, ![]() – плотность и удельная
теплоемкость соответственно.
– плотность и удельная
теплоемкость соответственно.
При
выполнении условия (1) распределение скоростей в расплаве является радиальным.
Обычно радиальное распределение скоростей между двумя вращающими цилиндрами
описывается как куэттовское течение жидкости [2], однако
для расплава в тигле, увлекаемого вращением выращиваемого кристалла, оно
оказывается неприменимым, поскольку не удовлетворяет условию обращения скорости
расплава в нуль на внутренней боковой поверхности тигля, и, кроме того,
обладает сингулярностью при ![]() , где
, где ![]() – радиальная
координата. В связи с этим в статье [3] было изучено радиальное поле скоростей
в расплаве, возникающее при вращении выращиваемого кристалла, которое
выражается следующей приближенной формулой
– радиальная
координата. В связи с этим в статье [3] было изучено радиальное поле скоростей
в расплаве, возникающее при вращении выращиваемого кристалла, которое
выражается следующей приближенной формулой
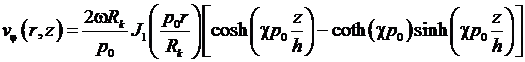 , (2)
, (2)
![]() ,
,
где ![]() – угловая скорость
вращения кристалла,
– угловая скорость
вращения кристалла, ![]() – его радиус,
– его радиус, ![]() – высота расплава,
– высота расплава, ![]() – отношение высоты фронта кристаллизации к радиусу кристалла,
и
– отношение высоты фронта кристаллизации к радиусу кристалла,
и ![]() – первый корень
уравнения
– первый корень
уравнения
![]() ,
,
где, в свою
очередь, ![]() ,
, ![]() – функции Бесселя n-го порядка, и
– функции Бесселя n-го порядка, и ![]() – отношения радиусов тигля и кристалла.
– отношения радиусов тигля и кристалла.
Имеются два
фактора, влияющие на устойчивость распределения скоростей (2). Во-первых,
наличие осевых температурных градиентов в расплаве приводит к появлению восходящих
потоков расплава, т.е. к появлению конвективной неустойчивости. Во-вторых,
радиальное распределение скоростей (2) может оказаться неустойчивым по
отношению к радиальным и осевым изменениям скорости расплава, что приводит к
гидродинамической неустойчивости, и, как следствие, к смене ламинарного
движения расплава на турбулентное.
Численные
оценки числа Рэлея для выращивания монокристаллов ниобата
лития методом Чохральского [4] показывают, что
критерий (1) не выполняется, т.е. расплав является конвективно неустойчивым.
Тем не менее, исследование гидродинамической неустойчивости расплава
представляет интерес, т.к. происходящие
при этом физические процессы имеют другую природу, чем те, которые порождают
конвективную неустойчивость, поэтому значение числа ![]() не связано с
гидродинамической неустойчивостью.
не связано с
гидродинамической неустойчивостью.
Для
исследования устойчивости распределения скоростей (2) по отношению к малым
возмущениям поля скоростей ![]() , т.е. гидродинамической устойчивости, запишем уравнение Навье-Стокса в цилиндрических
координатах
, т.е. гидродинамической устойчивости, запишем уравнение Навье-Стокса в цилиндрических
координатах ![]() для компонент скорости
жидкости [2,5]
для компонент скорости
жидкости [2,5]
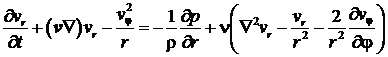 , (3)
, (3)
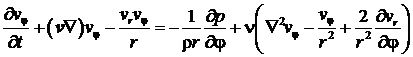 , (4)
, (4)
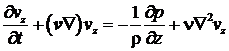 , (5)
, (5)
где
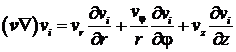 .
.
Уравнения
(1-3) дополняются уравнением непрерывности
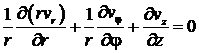 . (6)
. (6)
Для плоского
стационарного течения расплава ![]() , отлична от нуля только компонента
, отлична от нуля только компонента ![]() , давление
, давление ![]() , тогда из уравнений (3)-(6) получаем
, тогда из уравнений (3)-(6) получаем
![]() , (7)
, (7)
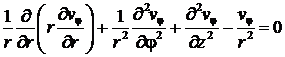 . (8)
. (8)
Функция ![]() , являющаяся осесимметричным (не
зависящим от
, являющаяся осесимметричным (не
зависящим от ![]() ) решением этой системы уравнений,
удовлетворяющим граничным условиям, соответствующим движению расплава в тигле
при выращивании кристаллов методом Чохральского,
приведена выше.
) решением этой системы уравнений,
удовлетворяющим граничным условиям, соответствующим движению расплава в тигле
при выращивании кристаллов методом Чохральского,
приведена выше.
Исследуем малые возмущения плоского осесимметричного движения расплава при помощи метода
медленно меняющихся амплитуд. Считая, что возмущения также являются плоскими, полагаем:
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() ,
,
![]() ,
,
![]() ,
, 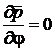 .
.
Так как ![]() , то параметр
, то параметр ![]() – целое число. Считаем далее, что слагаемые, содержащие
– целое число. Считаем далее, что слагаемые, содержащие ![]() ,
, ![]() , значительно меньше слагаемых, содержащих
, значительно меньше слагаемых, содержащих ![]() ,
, ![]() . Тогда уравнения (3) и (4) с учетом (7) приобретают вид
. Тогда уравнения (3) и (4) с учетом (7) приобретают вид
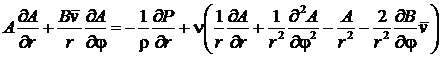 ,
(11)
,
(11)
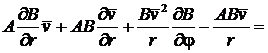
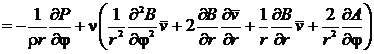 . (12)
. (12)
Уравнение
непрерывности (6) имеет вид
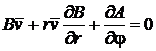 ,
,
Подставляя в
(11) и (12) разложения (9)-(10), получаем
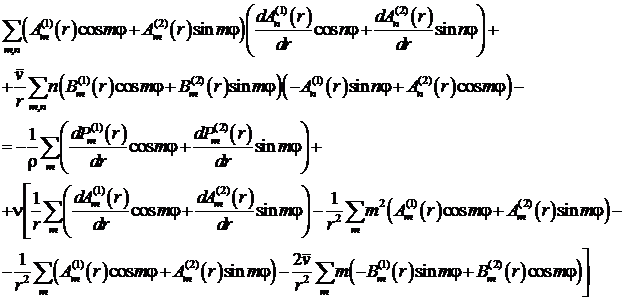 (13)
(13)
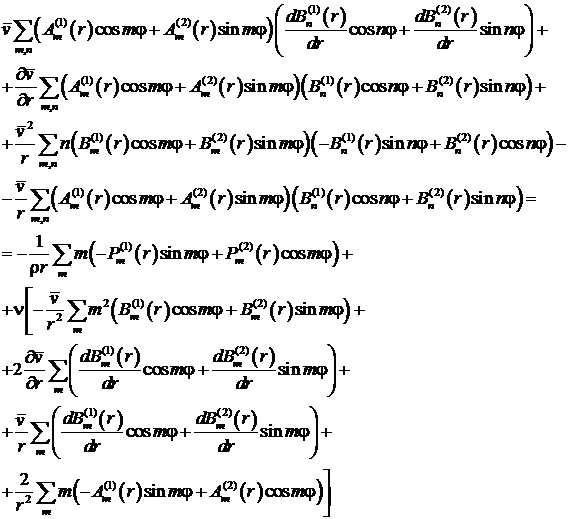 . (14)
. (14)
Умножаем уравнение (13) на ![]() ,
, ![]() и интегрируем по углу
и интегрируем по углу ![]() в пределах от 0 до
в пределах от 0 до ![]() . Для дальнейшего упрощения полученных уравнений считаем,
что в силу малости возмущений,
. Для дальнейшего упрощения полученных уравнений считаем,
что в силу малости возмущений, ![]() , т.е.
, т.е. ![]() , вследствие чего выражение (13) приводит к системе двух приближенных
уравнений
, вследствие чего выражение (13) приводит к системе двух приближенных
уравнений
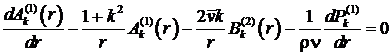 , (15)
, (15)
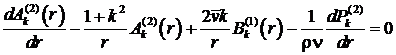 , (16)
, (16)
где ![]() – целое число.
Аналогичным образом, интегрируя уравнение (13) по углу
– целое число.
Аналогичным образом, интегрируя уравнение (13) по углу ![]() , получаем уравнение, отвечающие
значению
, получаем уравнение, отвечающие
значению ![]()
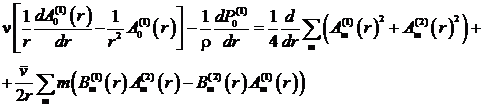 (17)
(17)
аналогичным
образом, преобразуя уравнение (14), получаем после отбрасывания малых слагаемых
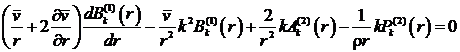 , (18)
, (18)
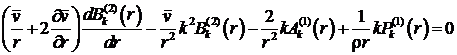 , (19)
, (19)
где ![]() . При
. При ![]() получаем уравнение
получаем уравнение
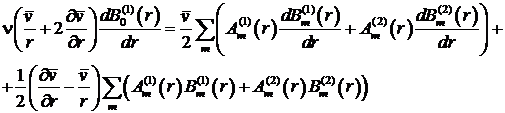 (20)
(20)
В линейном
приближении уравнения (17) и (20) имеют вид
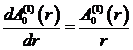 , (21)
, (21)
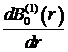 =0. (22)
=0. (22)
Граничные
условия выбираем в виде, отвечающем исчезновению малых возмущений на внутренней
стенке тигля
![]() ,
,
![]() .
.
В этом случае
можно считать, что ![]() ,
, ![]() , и из уравнений (21)-(22) получаем
, и из уравнений (21)-(22) получаем ![]() ,
, ![]() , что согласуется с распределением скоростей в нулевом
приближении [3].
, что согласуется с распределением скоростей в нулевом
приближении [3].
Преобразуем уравнение непрерывности,
которое запишем в виде
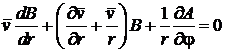 .
.
Разложив, как
и выше, величины ![]() и
и ![]() в ряды по тригометрическим функциям, получаем
в ряды по тригометрическим функциям, получаем
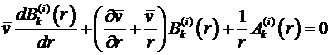 , (23)
, (23)
где ![]() .
.
Полагаем
далее ![]() ,
, ![]() , тогда система уравнений (15), (16), (18), (19), (23) запишется
в виде
, тогда система уравнений (15), (16), (18), (19), (23) запишется
в виде
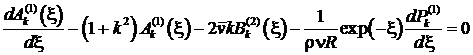 , (24)
, (24)
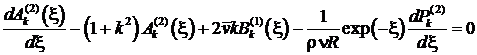 , (25)
, (25)
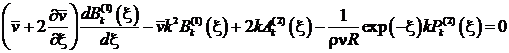 , (26)
, (26)
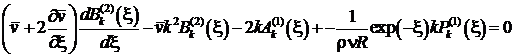 , (27)
, (27)
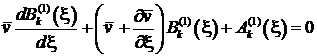 , (28)
, (28)
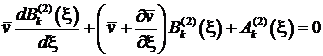 . (29)
. (29)
В
соответствии с общими методами исследования устойчивости движения несжимаемой
жидкости [6] ищем решение системы (24)-(29) в виде ![]() . Так как
. Так как ![]() , устойчивое движение жидкости отвечает значениям
характеристического показателя
, устойчивое движение жидкости отвечает значениям
характеристического показателя ![]() . Составляем характеристическую матрицу приведенной системы
. Составляем характеристическую матрицу приведенной системы

Численный
анализ секулярного уравнения, полученного с помощью
характеристической матрицы, позволяет определить области значений параметров
системы, отвечающие устойчивому плоскому ламинарному движению расплава в
тигле. Явный вид характеристической матрицы показывает, что, как и в большинстве
случаев, определяющим параметром,
определяющим смену режима движения расплава, является комбинация скорости
движения расплава ![]() , кинематической вязкости
, кинематической вязкости ![]() и радиуса тигля
и радиуса тигля ![]() , т.е. число Рейнольдса.
, т.е. число Рейнольдса.
Литература.
1.
Смирнов П.В., Антонов П.И. Отсутствие свободной
конвекции расплава в методе Чохральского в земных
условиях // Тезисы XII
Национальной конференции по росту кристаллов, 23-27 октября 2006 г.
2.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М., Наука,
1986, 733 с.
3.
Тумаев Е.Н., Гаража Е.В. Распределений скоростей в
расплаве при выращивании кристаллов методом Чохральского
// Физико-химический анализ свойств многокомпонентных систем [Электронный ресурс].
– Краснодар: КубГТУ, 2006 – Электронный научный
журнал. – вып.4. – Режим
доступа: http://kubstu.ru/fh/fams/st9.doc – Зарегистрировано НТЦ «Информрегистр»
1.03.2007 под номером 0420600011/0009
4.
Kitashima T., Liu L., Kitamura K., Kakimoto
K. Effect of shape of an inner crucible on convection of lithium niobate melt in a double-crucible Czochralski
process using the accelerated cruicible rotation
technique // Journal of Crystal Growth, 2004, 267, p.574-582.
5.
Слезкин Н.А. Динамика вязкой
несжимаемой жидкости. М., ГИТТЛ, 1955, 520 с.
6.
Гершуни Г.З., Жуховицкий Е.М.
Конвективная устойчивость несжимаемой жидкости. М., «Наука», 1972, 392 с.\
Поступила в редакцию 2 октября 2007 г.