Тренажер вертолета для подготовки лётного экипажа действиям в экстремальных ситуациях

 

Прошин Иван Александрович,

зав. кафедрой «Автоматизация и управление»,

Тимаков Владимир Михайлович,

доцент кафедры «Автоматизация и управление»,

Прошкин Виктор Николаевич,

кандидат технических наук, доцент кафедры «Автоматизация и управление».

Пензенская государственная технологическая академия.

 

Рассматриваются тренажёры для подготовки лётного состава пилотированию в чрезвычайных ситуациях  и, прежде всего, совершенствованию динамических стендов и управляемого гидропривода тренажёров вертолета с посадкой на воду. Определены требования к тренажёру и предложена методика выбора тренажёра. Исследован вопрос повышения точности отработки задающих воздействий посредством компенсации веса платформы динамического стенда.

 

Введение

 

Тренажерные технологии возникли и получили наибольшее распространение там, где ошибки при обучении на реальных объектах приводят к чрезвычайным последствиям, а их устранение –  к большим финансовым затратам: в военном деле, в авиации и космосе, в медицине, при ликвидации последствий стихийных бедствий, в атомной энергетике, высокотехнологичном производстве и т.д.

Отработка навыков пилотирования в экстремальных и аварийных ситуациях, отработка задач боевого применения авиации, спасение экипажей подводных лодок, катапультирую­щихся пилотов, рыбаков и др., терпящих бедствие, требует от лётных экипажей летательных аппаратов специальной подготовки в их управлении, которая может быть обеспечена только с использованием тренажёров. Силовое – акселерационное воздействие на пилота становится определяющим при выработке навыков пилотирования. Степень достоверности динамической имитации (имитации силового воздействия) полета во многом определяет совершенство современного авиационного тренажера (АТ).

Только с помощью имитаторов акселерационных воздействий (ИАВ), которые воспроизводят полетные перегрузки и угловые положения летательного аппарата, возможно моделировать полет самолета в условия опасных внешних воздействий: возмущенной атмосфере, обледенении самолета и др., а также при отказе систем самолета и частичном его разрушении. В чрезвычайных ситуациях полета возникают сложные пространственные перемещения и высокие перегрузки летательного аппарата, которые, воздействуя на пилота, становятся определяющими при выработке навыков пилотирования.

Современные авиационные тренажёры достаточно полно имитируют процессы взлета, посадки и всевозможные полетные ситуации в воздухе. Однако развитие авиации, расширение её возможностей, необходимость подготовки  экипажей к полётам в чрезвычайных ситуациях выдвигает новые проблемы и обуславливает всё более жёсткие требования к АТ. Одной из таких проблем является создание и совершенствование систем имитации колебаний вертолета с посадкой на взволнованную водную поверхность для обнаружения подводных лодок.

Основное внимание в данной работе уделено совершенствованию тренажёров для подготовки лётного состава пилотированию в чрезвычайных ситуациях  и, прежде всего, совершенствованию динамических стендов и управляемого гидропривода тренажёров вертолета с посадкой на воду.

 

1. Требования к тренажёру вертолёта

 

Для исключе­ния перевертывания находящийся на взволнованной водной поверхности вертолёт должен быть направлен строго под определенным углом по отношению к фронту волны, что определяет необходимость обучения, как пилотов, так и операторов других плавающих объектов, навыкам по управлению этими объектами.

Управление плавающими объектами, особенно вертолетом, весьма сложная и опасная операция, требующая принятия быстрых решений по удержанию курса и мгновенных реакций по изменению подъемной силы воз­действием на органы управления, поэтому при имитации процесса управле­ния приводные устройства, осуществляющие движение кабины тренажера, должны удовлетворять высокой точности отработки входного сигнала, быст­родействию и плавности движения.

Угловые положения   плоскости задаются тремя точками, не лежащими на одной прямой. Такую плоскость зададим для вертолета ли­нией обвода днища от воды в спокойном состоянии. Отметим, что линия об­вода для днища вертолета близка к форме круга, для днища самолета-амфи­бии приблизительно удлиненный эллипс и т.д.

Для задания различных угловых положений плоскости обвода днища вертолета, определим три точки на этой плоскости, образованные вписанным в нее равносторонним треугольником, вершины которого касаются линии обвода плоскости фюзеляжа. Воздействуя на эти точки приложенной силой, можно управлять отклонениями этой плоскости в любом направлении, а, следовательно, и отклонениями кабины тренажера.

На рис. 1 схематически изображен вертолет, находящийся на глад­кой водной поверхности, где линия обвода от касания днища вертолета – по­верхности воды обведена пунктирной линией. Вершины равностороннего треугольника (а, в, с), касающиеся линии обвода, определяют три точки си­лового воздействия следящих приводов динамического стенда на  кабину тренажера при имитации угловых отклонений вертолета от воздействия волн, зависящих от скорости ветра (определяющего бальность волнения) и направ­ления фронта волны относительно фюзеляжа.

 

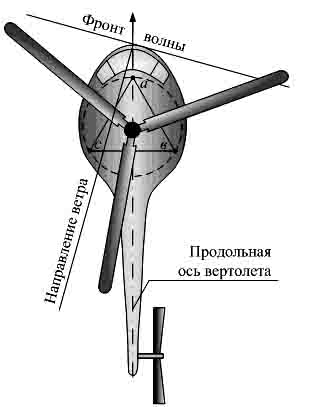
Рис. 1. Схема расположения вертолёта на водной поверхности.

 

При имитации движения кабины тренажера от воздействия волн на днище вертолета, точки (а, в, с) будут совершать возвратно-поступательные перемещения по вертикали, близкие к гармоническим колебаниям, но сдви­нутые по времени относительно друг друга в зависимости от направления фронта волны по отношению к фюзеляжу вертолета и скорости перемещения гребня волны.

На рис. 2 отражен механизм движения каждой точки (а, в, с) под воздействием следящих приводов, которые управляются сигналами,   вычис­ленными в соответствии с полученными уравнениями движения для каждой  из этих точек.

Точки (а, в, с) являются шарнирными точками крепления исполнитель­ных следящих приводов к кабине тренажера,  – угол направления ветра отно­сительно продольной оси вертолета.

Из анализа треугольников и  следует

;

.

,

,                                                                                      (1)

где А – длина стороны равностороннего треугольника abc.

 

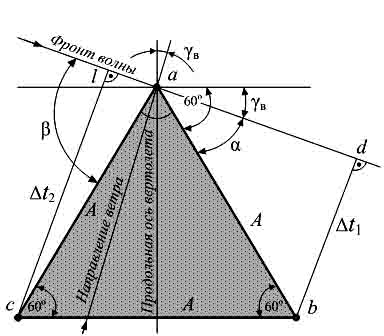
Рис. 2. Механизм движения вертолёта на водной поверхности.

 

Следовательно время  и  прохождения гребня волны на отрезках соответственно db и lc определяется выражениями

                                                                                                          (2)

где  – скорость перемещения гребня волны. 

Соотношения (2) с учетом (1) принимают вид:

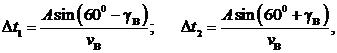                                                         (3)

Возвратно-поступательные перемещения шарнирных точек (а, в, с) с амплитудой L и заданной частотой  с учётом (3) будут описываться следующими уравне­ниями:

                                                                                                                

                                                                               

                                                                                 

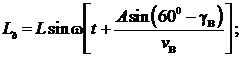
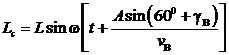
или в матричной форме

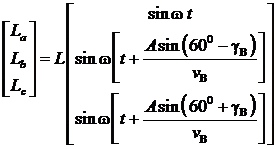.                                                                       (4)

Таким образом, задача по имитации движений кабины вертолёта от воздействия  волн сводится к перемещениям точек (a, b, c) по вертикалям в соответствии с уравнениями (4) для каждой из них. Для выполнения такой задачи необходим динамический  стенд, обеспечивающий угловые  движения по крену, тангажу и вертикали.

 

2. Анализ динамических стендов авиационных тренажёров

 

На рис. 3 и рис. 4 представлены отечественные динамические стенды авиационных тренажеров с шестью степенями свободы ДС6-1 и ДС6-1,5.

Движение подвижной платформы шестистепенного динамического стенда задается в трех точках воздействием на каждую шарнирно соединен­ную пару исполнительных гидроцилиндров привода.

 

Рис. 3. Динамический стенд ДС6-1.

 

Рис. 4. Динамический стенд ДС6-1,5.

 

Шестистепенной стенд представляет собой пространственно-кинема­тическую схему из шести взаимосвязанных  попарно исполнительных гидро­цилиндров следящих приводов, работающих в телесном угле до 70 градусов относительно вертикальной оси.

Такая конструкция устойчива от сваливания, скручивания относительно вертикальной оси и других несанкционированных перемещений подвижной платформы. Недостатком такой конструкции является взаимовлияние приводов на перераспределение массы подвижной платформы и размещенного на ней груза на каждой из приводов, что значительно  ухудшает работу и отрицательно влияет на дина­мические характеристики приводов. Для устранения этого недостатка требу­ется значительно увеличивать запас по усилиям приводов, а, следовательно, и потребляемую мощность.

На рис. 5 представлен трехстепенной динамический стенд (од­ной линейной по вертикали и двум угловым степеням свободы) типа ДС-3 с предельным угловым отклонением по тангажу.

Подвижные кинематические звенья этого стенда, сваренные из сило­вых пустотельных коробов, удерживают подвижную платформу от свалива­ния, скручивания и линейных перемещений в продольном и поперечном на­правлениях, воспринимая на себя возникающие при этом нагрузки.

 

Рис. 5.  Динамический стенд ДС-3 с  максимальным отклонением по тангажу.

 

На рис. 6 изображена кинематическая схема трёхстепенного стенда ДС-3. Подвиж­ная платформа стенда перемещается  тремя исполнительными гидроци­линдрами, каждый из которых шарнирно соединен с основанием и подвиж­ной платформой.  При такой конструкции каждый привод работает автономно, не оказы­вая заметного влияния на другие приводы, т.к. отклонение оси каждого ис­полнительного гидроцилиндра от вертикали в телесном угле, при максимальных угловых перемещениях подвижной платформы, не превышают 6 градусов, что видно из рис. 5.

 

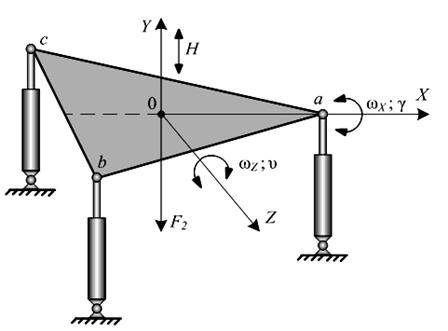
Рис. 6.  Кинематическая схема динамического стенда ДС-3.

 

Такая кинематика стенда практически исключает взаимное влияние на изменение (пере­распределение) усилий от веса подвижных частей на каждый гидропривод при их совместной работе.

 Одним из важных вопросов при создании динамических стендов явля­ется выбор приводных следящих устройств, задающих перемещения под­вижной платформе. Из существующих различных видов приводных уст­ройств наибольшее распространение получили электрические и электрогид­равлические системы. Причем,  электрогидравлические следящие приводы находят большее применение. К основным преимуществам гидравлических следящих приводов отно­сятся малые габариты и вес, а также высокое быстродействие (быстрота ре­акции системы на командный импульс), обусловленное, главным образом, малой инерцией подвижных частей и высокой силовой напряженностью.

Так, например, вес и объем гидравлических агрегатов составляет 15 – 20 % соответствующих параметров электрических агрегатов равновеликой мощности.

К преимуществам гидравлических систем можно отнести плавность и устойчивость движения, простоту предохранения оси перегрузок и обеспече­ния надежного демпфирования.

В таблице 1 приведены основные технические характеристики отечест­венных динамических стендов авиационных тренажеров с электрогидравли­ческими приводами.

 

Таблица 1.

Динамические стенды авиационных тренажёров.

Параметр	Тип динамического стенда
	ДС3	ДС6-1	ДС6-1,5
Максимальные линейные перемещения:
продольное, м	–	+0,93; -0,73	+1,38; -1,07
вертикальное, м	±0,55	+0,6; -0,78	0,088; -1,01
поперечное, м	–	±0,75	±1,12
Максимальные угловые перемещения:
тангаж, град	±24	±25	±25
крен, град	±23	±29	±28
рыскание, град	–	±27	±28
Максимальная линейная скорость, м/с	0,8	0,8	0,8
Максимальное линейное ускорение, м/с2	8	8	8
Максимальная угловая скорость, град/с	30	30	30
Грузоподъемность, кН (тс)	40(4)	50(5)	90(9)
Энергопотребление, кВА	70	120	180
Давление в магистрали нагнетания, МПа (кг/см2)	20 (200)	20 (200)	20 (200)
Количество степеней свободы стенда	3	6	6

 

Исходя из вышеизложенного, следует, что для имитации колебаний вертолета, находящегося на взволнованной водной поверхности, и обучения пилотированию вертолёта в экстремальных ситуациях достаточно использовать динамический стенд с тремя степенями свободы: две угловые по крену и тангажу, а третья по вертикали.

 

3. Выбор динамических стендов тренажёров

 

Необходимо отметить, что посадка вертолета на водную поверхность допустима с волнением менее 3-х баллов, при котором амплитуда колебаний (высота волны) составляет менее одного метра, что в основном определяет конструктивные требования к динамическому стенду. Из анализа таблицы 1 следует, что наиболее приемлемым является ди­намический стенд ДС-3 , изображенный на рис. 5.

Для определения соответствия параметров движения стенда ДС-3, при воспроизведении ускорений, параметрам движения от воздействия гармонических колебаний на реальный объект при волнении водной поверхности, представим график синусоидального движения, например, точки (а), изображенного на рис. 7 с учетом предельных значений стенда по перемещению и скорости движения штока гидроцилиндра.

 

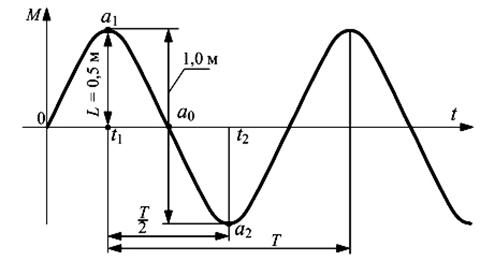
Рис. 7. Модель волнения водной поверхности.

 

Максимальное ускорение при движении точки (а) определим по значению второй производной от перемещения (4). Скорость перемещения  точки (а) определяется первой производной от перемещения

.                                                                                                        (5)

Вторая производная от перемещения – ускорение  точки (а)

.                                                                                                     (6)

Значение угловой частоты  в уравнениях (5), (6) определим, решая систему двух уравнений с двумя неизвестными  и .

 

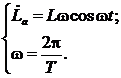
Откуда                                                                                                                              

.

Следовательно

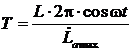.                                                                                                           (7)

Максимальная скорость  шарнирного узла (а) соответствует точке траектории движения  (рис. 7)  и определяется максимальной скоростью движения штока гидроцилиндра равной .

Учитывая, что при волнении до 3 баллов высота волны от гребня до впадины составляет менее 1 м, а располагаемый ход штока гидроцилиндра равен 1 м, следовательно можно принять значение , тогда в соответствии с (7)

;    .

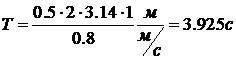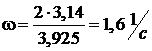Подставляя в уравнение (6) значение  определим максимальное ускорение воспринимаемое реальным объектом

.

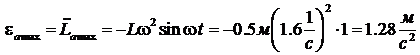Произведенные расчеты подтверждают возможности использования  стенда ДС-3 для подготовки пилотов вертолётов, так как согласно таблице 1 стенд ДС-3 способен воспроизводить ускорения до 8, превышающие требуемые ускорения величиной 1.28.

 

 4. Моделирование движения динамического стенда

 

Математическая модель механической части динамического стенда может быть представлена дифференциальными уравнениями (рис. 6) перемещений   шарнирных узлов с платформой с массами нагрузки  и действующими силами со стороны гидропривода  и со стороны платформы :

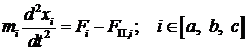.                                                                              (8)

Здесь в (8) за положительное направление движения принято движение вверх.

Для моделирования механической части динамического стенда на компьютере представим модель (8) в пространстве вектора состояний 

 

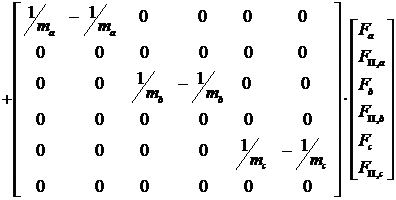                                          (9)

Проведём исследование влияния веса платформы на формирование силовых воздействий со стороны привода. Примем массы каждого шарнирного соединения вместе с платформой одинаковыми.  Для обеспечения движения массы  с постоянным ускорением   требуется усилие , что меньше веса платформы .  Для перемещения платформы динамического стенда с учётом веса платформы с ускорением  требуется усилие , которое более чем в два раза превышает усилие, необходимое для перемещения инерционной нагрузки при отсутствии веса платформы. 

На рис. 8 приведены результаты расчёта по модели (9) перемещений и скоростей платформы в шарнирном узле  при её движении вверх и вниз при действующих на платформу в каждом узле равных сил   для системы с компенсаций статической нагрузки [1 – 3] и без её компенсации.

Как видно из рис. 8 платформа в системе с компенсацией статической нагрузки приобретает ускорение , превышающее более чем в два раза ускорение платформы в системе без компенсации (), что позволяет повысить более чем в два раза быстродействие системы с компенсацией при одинаковых мощностях гидроприводов. Характеристики движения и по перемещению и по скорости для системы без компенсации несимметричны относительно оси времени, для системы с компенсацией обеспечивается полная симметрия характеристик.

Рис. 9 иллюстрирует  результаты расчёта по модели (9) перемещений и скоростей платформы в том же узле  при её движении вверх с одинаковыми для системы с компенсаций статической нагрузки и без её компенсации ускорениями . При этом в системе с компенсацией статической нагрузки обеспечивается движение как вверх, так и в низ с одинаковым ускорением, а характеристики движения симметричны.  В системе без компенсации ускорение () платформы при движении вниз значительно превышает её ускорение при движении вверх (), что и определяет несимметрию характеристик.

 

 

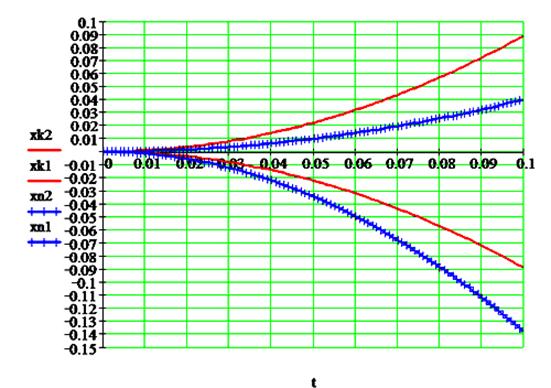
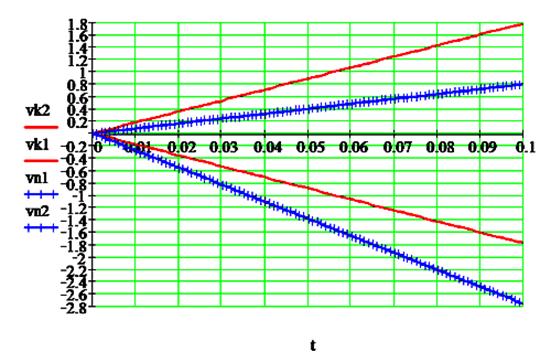
 Рис. 8.  Изменение перемещения и скорости в системе без компенсации и с компенсацией

при одинаковом силовом воздействии.

 

Для перемещения платформы с заданными ускорениями в системе с компенсацией со стороны привода необходимо обеспечить усилие , в то время как для создания такого же ускорения в системе без компенсации требуется значительно большее усилие .

 

 

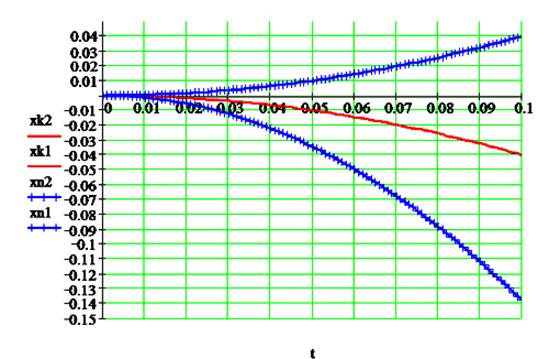
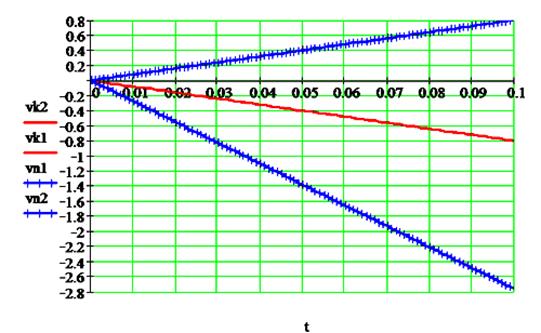
Рис. 9.  Изменение перемещения  и  скорости в системе без компенсации и с компенсацией

при одинаковом ускорении.

 

При движении платформы с меньшими ускорениями эффективность введения компенсации статической нагрузки значительно возрастает. Действительно, как следует из проведенных исследований для движения платформы с ускорением   в системе с компенсацией при массе платформы  требуется усилие  против  для системы без компенсации, т.е. в 8.664 раза меньше, чем в системе без компенсации. Аналогичные результаты получены и для других шарнирных точек.

 

Заключение

 

Отработка навыков пилотирования в экстремальных и аварийных ситуациях может быть обеспечена только с использованием тренажёров. Исходя из требований по имита­ции колебаний плавающих объектов, находящихся на взволнованной водной поверхности (гидросамолеты, самолеты амфибии, катера на воздушных подушках, противолодочные вертолеты для обнаружения под­водных лодок с определением их скоростей, направления движения и глу­бины погружения) для подготовки лётного состава могут быть использованы динамические стенды ДС-3. Разработанный гидропривод с компенсацией веса подвижной платформы позволяет повысить точность отработки задающих воздействий и приблизить нагрузки, создаваемые на стенде к реальным, уменьшить величину создаваемых гидроприводом усилий при сохранении быстродействия. Практическое использование разработанной системы при создании динамических стендов авиационных тренажёров для подготовки лётного состава  противолодочного вертолёта В – 14 с посадкой на воду,  показало её высокую эффективность, выразившуюся в более точном воспроизведении акселерационных воздействий, повышении управляемости и надёжности тренажёров.

 

Литература

 

1.             А.с. № 77429 / Мануйлович В.П., Тимаков В.М., Швецов П.Е.

2.             Прошин И.А., Прошкин В.Н., Тимаков В.М. Системный анализ магнитострикционных преобразователей параметров движений на крутильных магнитоупругих волнах для тренажеров транспортных средств. Надежность и качество. (I том) Труды международного симпозиума. Пенза, ПГУ, 2008. – С.458-462.

3.             Прошин И.А., Прошкин В.Н., Тимаков В.М., Баннов В.Я., Таньков Г.В., Селиванов В.Ф. Математическое моделирование гидроприводов авиационных тренажёров. Надежность и качество. (I том) Труды международного симпозиума. Пенза, ПГУ, 2008. – С.469-472.

 

Поступила в редакцию 21.11.2008 г.