УДК 548.11
Моделирование кооперативного движения
атомов в системе с симметрией плоской кристаллографической группы.
Тытик
Дмитрий Леонидович,
кандидат физико-математических наук,
старший научный сотрудник Института
физической химии и электрохимии РАН.
Предложена модель описания кооперативного движения атомов в симметричных системах, основанная на применении группового преобразования к точкам некоторой непрерывной кривой в фундаментальной области группы. Результатом этого преобразования является непрерывное многообразие правильных систем точек, которое может быть интерпретировано как возможное в симметричной системе кооперативное движение атомов.
Ключевые слова: области симметрии, компьютерное моделирование.
Введение.
Расположение атомов в кристаллической фазе всегда подчиняется некоторой пространственной группе, что является геометрическим выражением сложных процессов самоорганизации атомов вещества, которые пока недостаточно изучены. Если допустить, что групповое описание строения вещества это геометрический способ учета многочастичных взаимодействий в системе атомов, то можно попытаться описать некоторые процессы самоорганизации атомов, рассматривая групповые свойства без привлечения потенциалов взаимодействия атомов в системе. В последние годы для реализации самоорганизации наночастиц используют различные поверхностные технологии, например, пленки Ленгмюра-Блоджетт [1, 2]. Структура активных центров на поверхности описывается одной из плоских кристаллографических групп. Используя свойства группы, был построен новый тип преобразования [3], который может служить важным инструментом для изучения локальных кооперативных движений атомов и оценки энергетики соответствующей перестройки структуры. Предлагаемый метод реализован для 17 плоских кристаллографических групп.
Ремонт квартир и коттеджей в Геленджике. Для тех, кто ценит качество geldom.ru
Целью статьи является описание метода моделирования кооперативного движения атомов на примере системы с симметрией p6.
Движение
эквивалентных точек в симметричной системе.
История предлагаемого подхода берет начало в 1920-40-х годы, когда П. Ниггли опубликовал ряд работ [4, 5], посвященных классификации гомогенных и гетерогенных кристаллических структур. В качестве удобного инструмента анализа структуры Ниггли предложил использовать понятие областей симметрии элементов симметрии, кристаллической группы описывающей структуру вещества. По определению внутри области симметрии какого-нибудь элемента симметрии точки, эквивалентные в отношении этого последнего элемента, находятся на более близких расстояниях друг от друга, чем от всех других эквивалентных точек. При заданной метрике можно построить все области симметрии, принадлежащие к группе симметрии. Совокупность этих областей должна охватывать все пространство, занимаемое точечными положениями.
В
симметричных системах (молекулы, кластеры, поверхность на границе раздела фаз, твердое
тело), подчиняющихся какой-либо точечной, плоской или пространственной группе,
симметрично-эквивалентные атомы описываются совокупностью одной и более орбит
этой группы. В общем случае любую группу преобразований симметрии G можно считать состоящей
из операторов, каждый из которых действует на множестве A каких-либо конгруэнтных объектов,
в нашем случае конечного набора точек (атомов). Выберем в фундаментальной
области группы произвольную ориентированную непрерывную кривую длиной L, имеющую начальную и
конечную точки. Введем параметризацию, при которой каждой точке кривой
соответствует число l,
расстояние этой точки от начала кривой. На числовом отрезке 
определим
преобразование l=f(t), где 
, при котором любая точка из числового отрезка однозначно определяет
точку на кривой с координатами x(t),
y(t), z(t). Изменение значений параметра t от начала к концу
отрезка и наоборот позволяет менять порядок прохождения кривой.
Рассмотрим
преобразование F=G(x(t),y(t),z(t)) с областью определения 
, которое будет состоять в действии всех операторов группы G на координаты последовательных
точек кривой и получении многообразия (непрерывной последовательности) орбит Ai группы G. Другими словами, взяв
точку кривой в качестве положения базисного атома с координатами x, y, z остальные координаты атомов
получаются по формулам размножения правильной системы точек, содержащимся в
Интернациональных таблицах [6].
Определение. Если выбрать порядок прохождения точек кривой в фундаментальной области группы и к точкам кривой применить непрерывное преобразование F, то получится непрерывная последовательность правильных систем точек (многообразие), которую можно интерпретировать как непрерывную последовательность стадий движения правильных систем точек в двухмерном (трехмерном) пространстве.
Точки в симметричной системе могут занимать частные и общие положения, которые характеризуются степенями свободы. Точки с одной степенью свободы могут двигаться в пределах некоторой прямой, с двумя степенями свободы в пределах некоторой произвольной кривой плоскости внутри фундаментальной области группы. Если в симметричной системе с несколькими орбитами ввести связность как ближайшие расстояния между точками разных орбит, то можно поставить задачу нахождения такого многообразия, на котором преобразование F не нарушает связности между точками разных орбит в процессе взаимного движения точек. При преобразовании F длины связей в симметричной системе должны изменяться в достаточно узком диапазоне (условие сохранения связности).
Рассмотрим
реализацию предложенного метода моделирования движения на примере плоской группы
p6. Для этого
рассмотрим фундаментальную область группы p6 и учтем, вид теоремы Пифагора для гексагональной
сингонии:
,
последнее
слагаемое для плоской группы отсутствует. Тогда можно записать условия для
нахождения границы областей симметрии как систему уравнений квадратов
расстояний, записанных для пар элементов симметрии этой группы, например, 
. Здесь разными индексами обозначаются расстояния, на которые
соответствующие элементы симметрии оси (6-, 3- и 2-ого порядка) удаляют точку
№1, расположенную на искомой границе области симметрии (рис. 1).
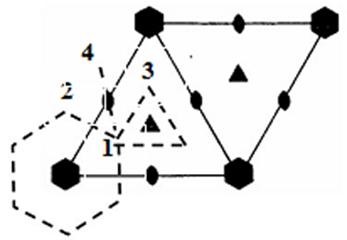
Рис. 1.
Фундаментальная область группы p6 с элементами симметрии (оси 2-, 3- и 6-ого порядка).
Точка № 1 принадлежит границе области симметрии для соответствующих
элементов симметрии. Точки № 2, 3, 4 получены размножением точки
№ 1 соответствующими элементами симметрии. Условие для определения границы
области симметрии записывается как уравнение для квадратов расстояний,
например, 
. Подстановка в это уравнение координат точек дает уравнение
кривой.
Аналогичные
уравнения можно записать для всех пар элементов симметрии в фундаментальной области
группы и получить комбинаторно полный набор уравнений, определяющих границы
фундаментальных областей симметрии плоской группы p6:
1) 3x2-3xy+3y2-4x+2y+1=0, 14) x2-xy+y2+x-2y=0,
2) 3x2-3xy+3y2-2x-2y+1=0, 15) x2-xy+y2-2x+y=0,
3) 3x2-3xy+3y2+2x-4y+1=0, 16) x2-xy+y2+2x-y=0,
4) 3x2-3xy+3y2+4x-2y+1=0, 17) x2-xy+y2-x-y=0,
5) 3x2-3xy+3y2+2x+2y+1=0, 18) x2-xy+y2+x+y=0,
6) 3x2-3xy+3y2-2x+4y+1=0, 19) 3x2-3xy+3y2-2x+y=0,
7) 2x2-2xy+2y2-3x+1=0, 20) 3x2-3xy+3y2-x-y=0,
8) 2x2-2xy+2y2-3y+1=0, 21) 3x2-3xy+3y2+x-2y=0,
9) 2x2-2xy+2y2+3x-3y+1=0, 22) 3x2-3xy+3y2+2x-y=0,
10) 2x2-2xy+2y2+3x+1=0, 23) 3x2-3xy+3y2+x+y=0,
11) 2x2-2xy+2y2+3y+1=0, 24) 3x2-3xy+3y2-x+2y=0,
12) 2x2-2xy+2y2-3x+3y+1=0, 25) x2-xy+y2-3x+3y+2=0,
13) x2-xy+y2-x+2y=0, 26) x2-xy+y2+3x-3y+2=0,
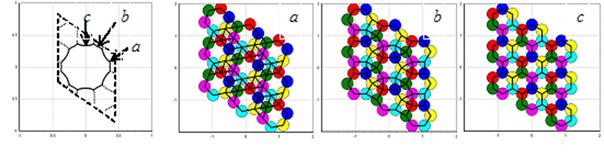
Рис.2.
Фундаментальная область плоской группы p6 с границами областей симметрии. Буквами a, b, c обозначены точки, групповое преобразование которых
соответствует описанию стадий кооперативного перехода, конфигурации a, b, c (показаны несколько ячеек).
На
рис. 2 изображена (слева) многосвязная граница областей симметрии в фундаментальной
области группы p6. Каждое из вышеприведенных уравнений определяет свой
фрагмент многосвязной границы. Все уравнения являются коническими сечениями, причем
с помощью алгоритма приведения Якоби можно установить, что они соответствуют
окружностями разных диаметров. Если использовать трансляцию, то общий вид
границ областей симметрии составится из фрагментов дуг пересекающихся окружностей
разного радиуса.
Для
моделирования движения атомов в системе с симметрией p6 применим групповое преобразование к точкам многосвязной
границы областей симметрии группы p6: 
. Несколько элементов непрерывного многообразия правильных
систем точек, изображенные на рис. 2, соответствуют стадиям кооперативного
движения атомов в симметричной системе.
Выводы.
Предложенная
модель кооперативного движения атомов позволяет рассмотреть реальную динамику
возможных молекулярных (атомных) процессов самоорганизации и является удобным
инструментом изучения локальных перестроек в симметричных системах, когда может
изменяться тип координации атомов или их радиус. Метод может быть применен
также для изучения границы перколяции в симметричных системах. Если использовать
внутренние координаты (длина связи, валентный и торсионный углы), то, используя
подходящий потенциал (например, как в методе молекулярной механики), можно
вычислить изменение энергии при кооперативной перестройке структуры.
Литература.
1. Современные проблемы физической химии. Москва, Издательский дом «Граница», 2005, 696 С.
2. Лен Ж.-М. Супрамолекулярная химия. Концепции и перспективы. Новосибирск, Наука СО РАН, 1998, 333 С.
3. Тытик Д.Л. // "XVIII Менделеевский съезд по общей и прикладной химии. Тезисы докладов в 5 томах. том.1 Достижения и перспективы химической науки", Москва, 2007, с.476.
4. Niggli P.
Krystallographische Und Strukturtheretische Grundbegriffe,
5. Ниггли П. Стереохимия, Москва, Издательство Иностранной литературы, 1949, 364 с.
6. International Tables for
X-ray crystallography.
Поступила в редакцию 22.04.2008 г.