Анализ работы и усовершенствование
системы автоматизированного управления сухой газоочистной установкой на примере
установки богословского алюминиевого завода.
Зотов
Сергей Александрович,
аспирант Уральского
Государственного Технического Университета – УПИ.
Руководитель: доктор технических наук, профессор
Лисиенко Владимир Георгиевич.
Процесс регенерации фильтров является
одним из основных технологических процессов “сухой” очистки газов,
поскольку именно в рукавных фильтрах осуществляется разделение твёрдой и
газообразных фаз при фильтрации пылегазовой смеси через фильтрующую
перегородку.
Анализ литературы [2, 6] показывает, что чаще всего на практике регенерация рукавов в рукавном фильтре производиться автоматически: либо при достижении критического перепада давления, либо в результате импульса от реле времени, как на рис. 1.
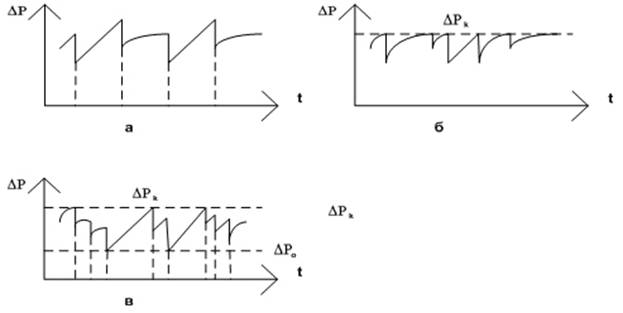
Рис. 1.
Схема регенерации фильтра: а –
временная; б – с фиксацией верхнего уровня перепада давления; в – с фиксацией
верхнего и нижнего уровней перепада давления.
При улавливании грубых пылей А.С. Мандрико и И.Л. Пейсаховым была найдена
зависимость между перепадом давления на рукавном фильтре и продолжительностью
периода между регенерациями [6].
Существенное влияние на качество очистки, на длительность эксплуатации
оказывает соответствие периода между регенерациями перепаду давления на
рукавном фильтре. Поэтому работа системы регенерации рукавных фильтров согласно
схем регенерации изображенных на рис. 1 малоэффективна, так как не учитывает
состояние запыленности рукавов.
Таким образом, нужно провести анализ, и модели Мандрико и Пейсахова, и
анализ экспериментальных графиков фильтров, после чего сравнить расчеты по
модели Мандрико и Пейсахова с результатом анализа экспериментальных графиков
фильтров. Это позволит разработать модель управления регенерацией рукавных
фильтров, выражающую зависимость периода между регенерациями от перепада
давления на рукавном фильтре.
Гидравлическое сопротивление фильтровальной перегородки (Па) может быть представлено суммой двух слагаемых [6]:
DР = DР1
+ DР2
= ![]() ,(1)
,(1)
где DР1 – постоянное сопротивление самой фильтровальной перегородки с учетом пыли, оставшейся на ней после регенерации, Па;
DР2 – переменное сопротивление накапливающегося на фильтровальной перегородке слоя пыли, удаляемого с нее в процессе регенерации, Па;
А – коэффициент сопротивления фильтровальной перегородки с слоем пыли, оставшейся на ней после регенерации, м-1;
В – коэффициент сопротивления слоя пыли, м/кг;
m – динамический коэффициент вязкости газа, Па´с;
Z – запыленность газа перед фильтром при рабочих условиях, кг/м3;
w – скорость фильтрования, м/с;
t – время, с.
В модели (1) численные значения коэффициентов А и В определяются только опытным путем [6].
Для
ориентировочных подсчетов путем обработки экспериментального материала для
частиц с dm £
20 мкм были получены следующие значения коэффициентов A и B.
Таблица 1.
Ткань –
лавсан арт. 217.
|
|
dm (мкм) |
A (м-1) |
B (м/кг) |
Вид пыли |
|
1 |
0,5 – 0,7 |
(13000 – 15000)·106 |
330·109 |
кремниевая, возгонная |
|
2 |
2,5 – 3,0 |
(2300 – 2400)·106 |
80·109 |
сталеплавильная, возгонная |
|
3 |
10 – 20 |
(1100 – 1500)·106 |
(6,5 – 16)·109 |
кварцевая, цементная |
Исследования показали, что чем мельче частицы улавливаемой пыли, тем выше коэффициенты А и В.
Для технических расчетов тканевых рукавных фильтров при улавливании грубых пылей (с dm > 20 мкм) А.С. Мандрико и И.Л. Пейсаховым была предложена модель [3]:
DР = 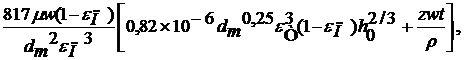 (2)
(2)
где dm – средний (медианный) размер частиц пыли, м;
eТ – пористость ткани, доли единиц;
eП
– пористость пыли, доли единиц; eп
= ![]() ;
;
ho – удельное гидравлическое сопротивление чистой ткани, Па;
r - плотность частиц пыли, кг/м3;
t – время между регенерациями, с.
Исходя из
модели (2), получаем DР = ![]() ,
где
,
где
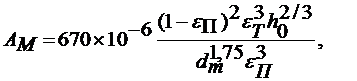 (3)
(3)
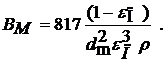 (4)
(4)
В формулах (3), (4) и ниже М – означает, что коэффициенты А и В определяются из модели Мандрико и Пейсахова (2).
Определим возможность применения формул (3) и (4) для вычисления коэффициентов А и В для расчетов рукавных фильтров при улавливании пылей с dm £ 20 мкм.
Из анализа функций АМ = f1(d) и ВМ = f2(d) и сопоставления значений коэффициентов А и В из табл. 1 с коэффициентами Ам и Вм рассчитанными по формулам (3) и (4) при одинаковых размерах частиц d получено, что в промежутке 0,5≤d≤10 мкм есть возможность использовать формулы (3) и (4), согласовав их с опытными данными табл. 1.
В нашем случае средний размер частиц пыли dm = 5 мкм [1, 2, 4, 5]. Из табл. 1 берем строку 2 с dm = 2,5 – 3,0 мкм близким к нашему. Из строки 2 имеем:
![]() мкм;
мкм; 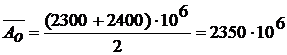 м-1.
м-1.
Тогда по
формуле (3) при d=![]() : АМо = 378·106 м-1.
Получено АМо = 378·106 ≠
: АМо = 378·106 м-1.
Получено АМо = 378·106 ≠ ![]() = 2350·106. Согласуем АМо и
= 2350·106. Согласуем АМо и ![]() .
.
![]() = СА·АМо => CA =
= СА·АМо => CA = ![]() / АМо = 2350·106/378·106 =
6,22.
/ АМо = 2350·106/378·106 =
6,22.
CA = 6,22 – поправочный коэффициент для АМ.
Принимаем,
что в некоторой окрестности т. ![]() = 2,75 мкм (куда входит и т. d = 5 мкм) формула А = CA·AМ для определения
коэффициента А в формуле (1) верна.
= 2,75 мкм (куда входит и т. d = 5 мкм) формула А = CA·AМ для определения
коэффициента А в формуле (1) верна.
По формуле (4)
при d=![]() BМo = 9,88·109 м/кг.
BМo = 9,88·109 м/кг.
Получено ВМо
= 9,88·109≠![]() = 80·109; Согласуем ВМо и
= 80·109; Согласуем ВМо и ![]() .
.
![]() =СВ·ВМо => СВ =
=СВ·ВМо => СВ = ![]() /ВМо = 80·109/9,88·109 = 8,1.
/ВМо = 80·109/9,88·109 = 8,1.
СВ = 8,1 – поправочный коэффициент для ВМ.
Принимаем,
что в некоторой окрестности точки ![]() = 2,75 мкм (куда входит и точка d = 5 мкм) формула В = CB·BM
для определения коэффициента В в формуле (1), верна.
= 2,75 мкм (куда входит и точка d = 5 мкм) формула В = CB·BM
для определения коэффициента В в формуле (1), верна.
Из формулы (1) при А = СА·АМ и В = СВ·ВМ получаем
DРМ
= ![]() .(5)
.(5)
Обозначим а =
![]() ; в =
; в = ![]() тогда
тогда
DРМ = а+в·t . (6)
Находим значения коэффициентов а и в в формуле (6) для нашего случая: d=5 мкм; εТ; ho – для иглопробивного фильтровального полотна; скорость фильтрования w1 = 1,3 м/мин; w2 = 1,5 м/мин.
а1 = 908 Па; в1 =6,85 Па/мин.
а2 = 1047 Па; в2 =9,12 Па/мин.
Т.о. получены линейные функции:
DР1 = а1+в1·t = 908 + 6,85·t при w1 = 1,3 м/мин;
DР2 = а2+в2·t = 1047 + 9,12·t при w2 = 1,5 м/мин.
Для определения функциональной зависимости гидравлического сопротивления (∆Р) фильтра от времени (t), рассмотрим экспериментальные графики, снятые на каждом 21 работающем фильтре. Каждый экспериментальный график имеет два участка. 1 участок – регенерация включена. Автоматика поддерживает ∆Р в фильтре приблизительно на одном уровне. 2 участок – регенерация отключена. В это время ∆Р в фильтре растет.
Каждый
участок экспериментального графика имеет вид ломаной линии отрезки, которой
соединяют точки (ti;
∆Рi) i = ![]() через одну минуту. N – число точек,
рассматриваемых на участке. При анализе графика фильтра 10 получено, что зависимость
∆Р от t
функциональная линейная и на 2 участке с отключенной регенерацией имеет вид: DР10
= 998 + 7,5·t = а10
+ в10·t.
через одну минуту. N – число точек,
рассматриваемых на участке. При анализе графика фильтра 10 получено, что зависимость
∆Р от t
функциональная линейная и на 2 участке с отключенной регенерацией имеет вид: DР10
= 998 + 7,5·t = а10
+ в10·t.
Аналогично
были найдены линейные функции и для остальных фильтров DРК = аК
+ вК·t к = ![]() (к ≠ 6, 9, 22, 10).
(к ≠ 6, 9, 22, 10).
Для сопоставления результатов полученных при анализе экспериментальных графиков с результатами полученными при использовании модели Мандрико и Пейсахова (с поправочными коэффициентами СА=6,22 и СВ=8,1), формула 5, определены средние значения коэффициентов а и в, и найдены:
1. Средняя функция DРМ =
¦(t) при расчете по модели Мандрико и Пейсахова.
![]() Па.
Па.
2. Средняя функция 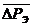 =¦(t) при расчете
по экспериментальным графикам фильтров.
=¦(t) при расчете
по экспериментальным графикам фильтров.
![]() =
=![]() =985 + 7,48·t Па.
=985 + 7,48·t Па.
Сопоставлены
средние функции 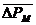 =¦(t) и
=¦(t) и 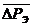 =¦(t).
=¦(t).
Определено,
что ![]() на 0,7 %
на 0,7 %
![]() на 6,4 %.
на 6,4 %.
![]() на 0,7 % при t = 1 мин.
на 0,7 % при t = 1 мин.
![]() на 0,4 % при t = 5 мин.
на 0,4 % при t = 5 мин.
Вывод: из
сравнения результатов расчета по модели Мандрико – Пейсахова (с поправочными
коэффициентами) с результатом анализа экспериментальных графиков 21 фильтра,
следует, что оба способа определения зависимости DР = ¦(t) достаточно хорошо
согласуются друг с другом.
Промежуток времени между импульсами на регенерацию (tИ) определяется только экспериментально. В нашем случае для заданного перепада давления на фильтре 900 – 1200 Па опытным путем были найдены соответствия:
∆Рmin = 900 Па à tи.max = 300 c.
∆Рmax = 1200 Па à tи.min = 60 c.
Находим функцию tИ = ¦(DP) при DPmin ≤ DP ≤ DPmax принимая, что зависимость tи от DP линейная. Получено:
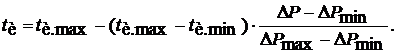 (7)
(7)
Промежуток времени (tИ) между импульсами на регенерацию при ∆P = a + b∙t, используя формулу (7), равен:
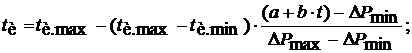 (8)
(8)
где а = ![]() ; в =
; в = ![]()
Подставив значения в формулу 7, получим:
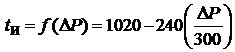 .
.
Было принято:
При ∆Р
< ∆Рmin
= 900 àtи = tи.max = 300 c. ![]() (Па); t(с)
(Па); t(с)
При ∆Р > ∆Рmax = 1200 àtи = tи.min = 60 c.
Таким образом, была получена составная функция (tи в минутах):
tи =
ƒ(∆Р) = 
![]() (Па); t(мин) . (9)
(Па); t(мин) . (9)
Из функций tИ = ¦И(DP) и 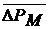 = ¦М(t) определим интервал оптимальных значений ∆P: (986; 1018) Па. При
∆P < 986 (Па) и ∆P > 1018 (Па) эффективность работы фильтра уменьшается из – за
нарушения целостности фильтрующего пылевого слоя.
= ¦М(t) определим интервал оптимальных значений ∆P: (986; 1018) Па. При
∆P < 986 (Па) и ∆P > 1018 (Па) эффективность работы фильтра уменьшается из – за
нарушения целостности фильтрующего пылевого слоя.
Точка
пересечения графиков функций tИ
= ¦И(DP) и ![]() = ¦М(t) в интервале оптимальных
значений ∆P
определяет то значение ∆Pопт,
которое будет поддерживать (в среднем) автоматика фильтра. Решая систему
уравнений получим:
= ¦М(t) в интервале оптимальных
значений ∆P
определяет то значение ∆Pопт,
которое будет поддерживать (в среднем) автоматика фильтра. Решая систему
уравнений получим: ![]() .
.
Таким
образом, функции tИ
= ¦И(DP) и ![]() = ¦М(t) применены для определения:
= ¦М(t) применены для определения:
1. промежутка оптимальных давлений эффективной работы фильтра;
2.
оптимального давления ![]() (из оптимального
промежутка), которое будет поддерживаться в фильтре.
(из оптимального
промежутка), которое будет поддерживаться в фильтре.
Составная функция, то есть зависимость промежутка времени между импульсами на регенерацию от перепада давления в фильтре и функция DР = а+в·t, то есть, линейная зависимость перепада давления в фильтре от времени, использованы при разработке алгоритмов программ автоматического управления и диагностики системы управления регенерацией рукавных фильтров и создание АСУ ТП регенерации рукавных фильтров.
Литература.
1. Технологическая инструкция – очистка газов отходящих от электролизеров корпусов электролизного цеха. ТИ БАЗ – 30 – 26 – 2006
2. С.Б. Старк – Газоочистные аппараты и установки в металлургическом производстве. «Металлургия» М. 1990 – 400 с.
3. М.Г. Мазус, А.Д. Мальтин, М.Л. Моргулис – фильтры для улавливания промышленных пылей. Машиностроение М. 1985 – 240 с.
4. Г.М. Гордон, И.Л. Пейсахов – Пылеулавливание и очистка газов в цветной металлургии М. Металлургия 1977 – 456 с.
5. Г.М. – А. Алиев Техника пылеулавливания и очистки промышленных газов. Справочник. Металлургия М. 1986 – 544 с.
6. М.Г. Ладыгичев, Г.Я. Бернер – Зарубежное и отечественное оборудование для очистки газов. Справочник. «Теплотехник» М. 2004 – 694 с.
Поступила в редакцию 11 февраля