Использование метода динамического программирования и его оптимизация при решении задач управления проектами.

 

Бекмурзаев Владий Александрович,

кандидат технических наук, профессор,

Шеховцов Андрей Алексеевич,

аспирант, действительный член PMI, сертифицированный PMP,

Московский Государственный Технический Университет «Станкин».

 

В течение нескольких последних десятилетий сформировалась новая область науки и знаний – управление проектами (Project Management). Под термином «проект» понимают ограниченное во времени целенаправленное предприятие, имеющее требования к привлекаемым ресурсам и качеству конечных результатов и предназначенное для создания уникальных продуктов, услуг или результатов. Таким образом, управление проектами – это приложение знаний, опыта, инструментов и методов к операциям проекта для удовлетворения требований, предъявляемых к проекту [1].

Управление проектами сегодня – это важнейший инструмент управления не только созданием новых продуктов и услуг, но и осуществлением целенаправленных изменений в рамках отдельных организаций, предприятий, а также целых социально-экономических и организационных систем. Сложно найти такую область деятельности человечества, где не использовались бы проекты. В частности управление проектами широко используется при создании и внедрении автоматизированных информационных систем управления ресурсами предприятия (в том числе управлением финансово-хозяйственной деятельностью и технологическими процессами).

Любой проект имеет определенную структуру – набор задач (операций/работ) или подпроектов, взаимоувязанных между собой, выполнение которых обеспечивает получение требуемого результата проекта.

Управление проектами ставит перед исследователями и руководителями проектов ряд нетривиальных задач, решение которых в общем случае не всегда оптимально или отсутствует вовсе. Таким образом, среди них можно выделить задачи ресурсного планирования, оптимального распределения ресурсов, минимизации упущенной выгоды, оптимизации проектов по стоимости и пр. Руководители проектов, сталкиваясь с подобными задачами в своей практике, зачастую действуют на основе своего опыта или по наитию.

Архитектурные фасадные элементы

Производство любых элементов по чертежам заказчика

vlando.ru

Фотоомоложение

фотоомоложение

idealistclinic.ru

На сегодняшний день теория управления проектами является бурно развивающимся разделом теории управления социально-экономическими системами. Можно выделить несколько различных направлений в управлении проектами.

Во-первых, это – модели календарно-сетевого планирования и управления (КСПУ), с появления которых и зародилось управление проектами.

Во-вторых, это – "качественный" подход к управлению проектами, близкий по своей методологии к менеджменту организаций и развиваемый, в основном, зарубежными учеными.

И, наконец, в-третьих, это – "количественный" подход, основывающийся на анализе и синтезе математических моделей механизмов управления проектами (процедурах принятия управленческих решений) и развиваемый, в основном, отечественными учеными [2]. Настоящая статья исследует аспекты количественного подхода.

Развитие общества, экономики, организации, да и жизни отдельного человека можно представить себе как совокупность дискретных процессов с заданными конечными целями, протекающими в условиях ограниченного времени и ограниченных ресурсов. Человеку удобно делить процесс своей деятельности на локальные процессы, которые требуют для своей реализации специальных методов управления [3]. В основу методов управления проектами заложено представление проекта в виде сетевого графика, отражающего зависимость между различными операциями проекта. Сложностью решения дискретных задач управления проектами (задач дискретной оптимизации) заключается  в том, что число допустимых решений экспоненциально растет с ростом размерности задачи n. Поэтому простой перебор всех решений невозможен при больших n. В то же время эти задачи относятся, как правило, к классу NP-полных задач, для которых не существует методов их точного решения, отличных от перебора.

Одной из актуальных задач управления проектами является задача о выборе наиболее приоритетных работ для выполнения из общего набора работ при заданном ограничении на общее время выполнения.

Данную задачу целесообразно решать методом динамического программирования, дающим точное решение. В основе метода динамического программирования лежит сведение задачи оптимизации к задаче определения экстремальной траектории (минимальной или максимальной длины) в некотором специальным образом построенном семействе возможных траекторий. В соответствии с принципом оптимальности Беллмана: любой участок оптимальной траектории оптимален [4]. В случае дискретных задач метод динамического программирования сводится к определению пути максимальной или минимальной длины в специальным образом построенной сети [5].

В качестве примера рассмотрим комплекс независимых работ проекта, с заданным временем выполнения каждой работы t­_i и полезностью u_i. Под полезностью работы будем понимать число работ, связанных с данной работой, которые становятся доступными для выполнения после завершения текущей работы.

Требуется выбрать подмножество работ M так, чтобы их суммарная полезность

                         (1)

была максимальной при ограничении на общее время выполнения T:

                                  (2)

Способ построения сети рассмотрим на примере из пяти работ, данные о полезности и времени которых приведены в таблице 1.

 

Таблица 1.

Данные примера.

i	1	2	3	4	5
ui	4	7	2	7	9
ti	3	4	2	5	7

 

Положим T = 10. Строим на плоскости систему координат, ось которой соответствует работам, а вторая – времени их выполнения. По оси работ отмечаем номера работ 1..5 (рис. 1). Из начала координат проводим две дуги: одна – горизонтальная в точку (1, 0), а другая – наклонная в точку (1, 3), где 3 – время выполнения первой работы. Первая дуга соответствует случаю, когда первая работа не выполняется, а вторая – когда выполняется. Из каждой полученной точки (1, 0) и (1, 3) проводим также по две дуги для второй работы. Получаем четыре точки (2, 0), (2, 4), (2, 3) и (2, 7), соответствующие четырем возможным вариантам для двух работ. Продолжая таким образом, получим сеть, приведенную на рис. 1, содержащую множество D всех возможных решений задачи.

 

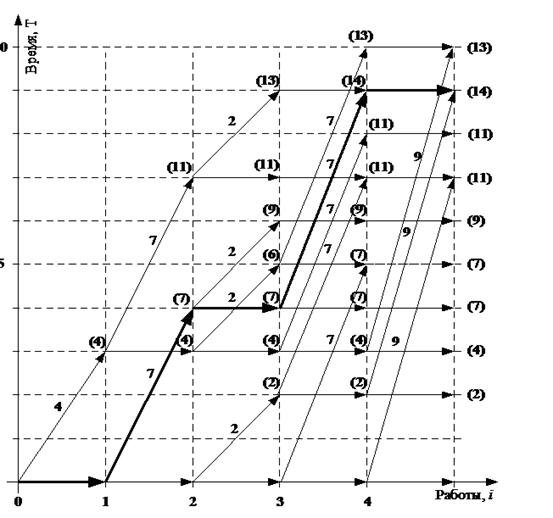
Рис. 1.

Метод динамического программирования.

 

Очевидно, что любой путь в сети, из начальной вершины 0 в одну из конечных вершин соответствует некоторому набору работ. И наоборот, любому набору работ, с общим временем выполнения не более 10 однозначно соответствует путь в сети, соединяющей начальную вершину с одной из конечных. Значение координаты по второй оси равно суммарному времени выполнения работ. Примем длины горизонтальных дуг равными 0, а длины наклонных равными полезности соответствующей работы. В этом случае длина пути, соединяющего начальную вершину с одной из конечных, равна суммарной полезности соответствующего набора работ. Таким образом, задача свелась к определению пути, имеющего максимальную длину. Путь максимальной длины выделен на рис. 1 жирными дугами; суммарная полезность U равна 14.

При решении данной задачи методом динамического программирования число допустимых решений равно 2ⁿ. Таким образом, для данного примера число путей в сети равно 32, а при большом n перебор всех возможных вариантов решений становится весьма трудоемким.

Возможное улучшение метода – использование комбинации эвристического алгоритма и метода динамического программирования, которая выглядит следующим образом:

Шаг 1. Введем понятие коэффициента полезности работы K^u_­, определяемого следующим образом:

                                              (3)

Вычислим K^u_­ для каждой работы и ранжируем работы по убыванию K^u_­. Из получившейся последовательности выбираем первые k работ, сумма t_i которых удовлетворяет формуле (2). Таким образом, множество D возможных решений разбивается на два подмножества: одно D₁ – в котором, одновременно не используются работы, не попавшие в набор из k работ; второе подмножество D₂ содержит все остальные варианты решений.

Очевидно, что полученный набор из k работ (табл. 2) является оптимальным решением в D₁ и локально-оптимальным решением в D, а с некоторой долей вероятности – оптимальным  в D (в данном примере полученное локально-оптимальное решение из 2-й и 4-й работ с суммарной полезностью равной 14 по случайности является оптимальным, в чем можно убедиться, отыскав его на рис. 1).

 

Таблица 2.

Локально-оптимальное решение.

i	2	4	1	5	3
Kui	1,75	1,40	1,33	1,29	1,00
ti	4	5	3	7	2

 

Шаг 2. Предположим, что в отброшенных работах есть комбинации, которые дают более оптимальное решение, чем решение в D₁. Рассмотрим подмножество решений D₂, применяя метод динамического программирования для всех комбинаций, где работы 1, 5 и 3 не исключаются одновременно (рис. 2). Для наглядности работы 1, 5 и 3 были перемещены в начало оси работ.

 

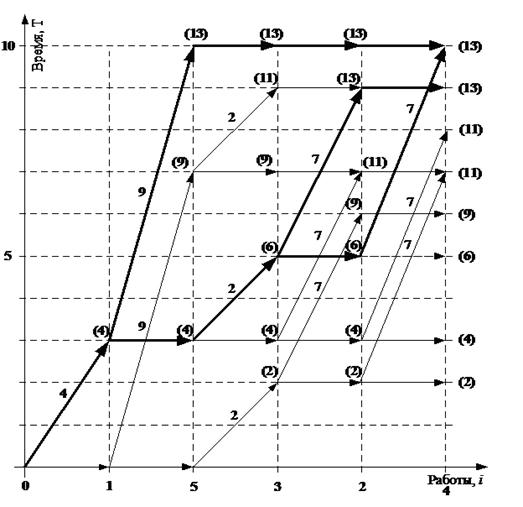
Рис. 2.

Улучшенный метод динамического программирования.

 

Оптимальные решения множества D₂ выделены жирными дугами на рис. 2; при этом полезность оптимальных решений равна 13, что меньше полезности оптимального решения множества D₁. Следовательно, набор из 2-й и 4-й работ является оптимальным решением задачи. При этом стоит отметить, что число допустимых решений множества D₂ на 2^k меньше, чем число решений в D. Таким образом, использование метода динамического программирования в комбинации с вышеизложенным эвристическим алгоритмом позволяет:

·                     во-первых, без использования рутинных операций по перебору сразу получить как минимум локально-оптимальное решение задачи;

·                     во-вторых, сократить количество переборов до 2ⁿ-2^k при поиске оптимального решения.

В заключении перечислим основные полученные результаты:

1.       Показано применение метода динамического программирования Беллмана к решению задачи о выборе приоритетных работ.

2.       Предложен новый метод решения задач дискретной оптимизации, заключающийся в улучшении метода динамического программирования за счет использования эвристических алгоритмов.

3.       Дана оценка сокращения количества комбинаций для перебора при поиске точного решения за счет использования эвристических алгоритмов в методе динамического программирования.

 

Литература.

 

1. Руководство к Своду знаний по управлению проектами. (Руководство PMBOK®). Третье издание. Издание на русском языке. – Project Management Institute, Inc., 2004.

2. Коновальчук Е.В., Новиков Д.А. Модели и методы оперативного управления проектами. – М.: ИПУ РАН, 2004. – 63 с.

3. Бурков В.Н., Квон О.Ф., Цитович Л.А. Модели и методы мультипроектного управления. М., Препринт / ИПУ РАН, 1997. – 62 с.

4. Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование. – М.: Наука, 1969.

5. Математическое основы управления проектами: Учеб. пособие / Баркалов С.А., Воропаев В.И., Секлетова Г.И. и др. Под ред. В.Н. Буркова. – М.: Высш. шк., 2005. – 423 с.

 

Поступила в редакцию 26.02.2008 г.