Расчёт соответствия позиционным допускам группы отверстий без указанной базы методом наименьших квадратов.

Косаревский Сергей Владимирович,

аспирант Санкт-Петербургского Института Машиностроения (ЛМЗ-ВТУЗ),

ведущий инженер Центральной Лаборатории Измерительной Техники при ОАО «Ижорские заводы».

1. Введение.

«Многонаправленный позиционный допуск для группы отверстий без указания базы, заданный как циллиндрическое поле, подразумевает наилучшую посадку (плоские вращение и перемещение)». [1]

Под плоским вращением и перемещением будем понимать такое преобразование координат, при котором:

где:  – радиус-вектор исходной точки – центра отверстия (полученный с координатно-измерительного прибора);

α – угол поворота;

 – вектор перемещения;

– векторная функция, поворачивающая радиус-вектор  на угол α.

Далее мы будем называть векторную функцию  - посадкой.

Прежде чем приступить к формулировке задачи, определим векторную функцию . Она представляет собой аффинное преобразование вращения на плоскости вокруг начала координат и легко выражается в матричном виде как:

Теперь можно дать формальную постановку задачи обозначенной в заглавии статьи.

2. Постановка задачи и метод наименьших квадратов.

Одной из основополагающих работ, в которой сформулирована задача поиска преобразования между двумя множествами точек и предложено её решение в замкнутой форме, является статья [3], в которой рассматривается объёмный случай применительно к фотограмметрии. Мы же будем рассматривать только проекции точек на плоскость и используем данный метод для выполнения расчёта по результатам плоских координатных измерений. В отличии от применённых для трёхмерного случая в [3] единичных кватернионов мы будем задавать плоское вращение с помощью ортогональной матрицы 2x2.

За численный критерий оптимальности посадки целесообразно принять минимальное значение суммы квадратов отклонений измеренного положения каждого из отверстий[1] от их номинального положения. Т.е:

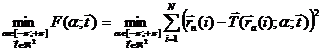
где:  - сумма квадратов отклонений отверстий, подлежащая минимизации;

N - количество точек;

 - номинальный 2D радиус-вектор точки – центра отверстия;

 - измеренный 2D радиус-вектор точки – центра отверстия.

Основной трудностью на пути решения задачи является то, что функция  это функция двух переменных (или же трёх вещественных переменных). Посмотрим, что можно предпринять в этом отношении. Цeлeсообразно ввести новые системы координат для каждого из множеств точек, такие, что центроиды каждого множества точек принять за начало соответствующей системы координат. Тогда можно воспользоваться следующей теоремой:

Теорема Хорна о центроидах: (без доказательства; общую математическую формулировку можно найти в [3]) При минимуме  центроиды множеств точек  и  совпадают.

На практике это означает, что угол поворота α и вектор переноса  являются независимыми величинами. Более того, из теоремы следует, что в некоторой системе координат S, в которой центроиды обоих множеств точек совпадают, искомое значение перемещения равно нулю. Для перехода в эту систему координат, нужно осуществить параллельный перенос измеренных точек на вектор -, а номинальных точек на вектор -,

где:  - центроид множества точек ;

 - центроид множества точек .

Воспользовавшись данным результатом и приняв новые координаты точек в системе координат S:

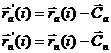
мы сводим функцию  к функции одной переменной. Подставляя явные выражения для посадки  и функции поворота системы координат , окончательно будем иметь:

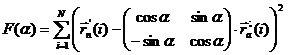
3. Практический расчёт.

Для практических вычислений удобно разложить полученные выше общие векторные формулы на отдельные компоненты X и Y, а так же помня, что скалярный квадрат вектора равен квадрату его длины, переписать F(α) в виде системы функций:

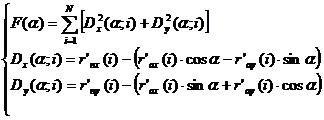
В качестве исходных данных при расчёте позиционных отклонений нам потребуется формула для вычисления производной  и начальное значение угла α отличное от 0. Для угла α, следуя общей рекомендации, примем значение равное 1. А что касается производной , то получение формулы для неё тривиально.

В таком виде удобно использовать численные методы оптимизации для минимизации функции F(α). В реализации автора был применён алгоритм Левенберга-Маркардта [2]. Возможно применение и других методов, равно как и использование вместо производной  конечной разности , где величина Δ меньшей требуемой точности вычислений.

После численной минимизации F(α) мы получаем значение параметра α при котором функция принимает своё минимальное значение (α_M). Теперь можно использовать полученное значение α_M для вычисления отклонений  каждого отдельного отверстия от своего номинального положения.

Очевидно, что данное отклонение для i-ого отверстия равно:

Поскольку на чертеже величины позиционных допусков указываются в диаметральном выражении, необходимо удвоить значение отклонения:

Остаётся только сравнить полученные значения  с величиной позиционного допуска , указанного на чертеже детали.

Литература.

1.         ГОСТ Р ... (ИСО 5458:1998) (Проект, I редакция) «Основные нормы взаимозаменяемости. Допуски формы и расположения поверхностей. Установление позиционных допусков ISO 5458:1998», М., Стандартинформ, 2007.

2.         Лоусон Ч., Хенсон Р., «Численное решение задач методом наименьших квадратов», М., Наука, 1986.

3.         B. K. P. Horn, «Closed-Form Solution of Absolute Orientation Using Unit Quaternion, Journal of the Optical Society Of America», Vol. 4, No. 4, pp. 629-642, 1987.

Поступила в редакцию 9 января 2008 г.