Критерии селекции моделей идентификации при использовании метода k-средних для решения диагностических задач

 

Калмыков Алексей Андреевич,

кандидат технических наук, доцент,

Сысков Алексей Мстиславович,

аспирант.

Кафедра радиоэлектроники информационных систем Уральского государственного технического университета – УПИ.

 

В данной статье рассматривается селекция моделей идентификации с использованием метода k-средних на примере анализа изображений «частотного сканирования» радиограмм головного мозга человека[1].

Методы кластерного анализа, к которым относится метод k-средних, находят широкое применение на начальных этапах анализа данных и построения модели идентификации[2].

Метод k-средних принято использовать при проверке гипотез, основанных на допущениях, лежащих в основе эмпирической гипотезы компактности[3]. Метод обладает рядом преимуществ

-                   устойчивость к шумам;

-                   возможность применять на малых в сравнении с размерностью признакового пространства обучающих выборках.

Однако возможности количественно оценить значимость результатов метода k-средних ограничены. Анализ средних значений и F-статистики – это, пожалуй, всё, чем располагает исследователь. При решении задачи селекции моделей этих критериев недостаточно.

Общий подход к селекции моделей и объективному кластерному анализу сформулирован в работах Ивахненко А.Г. и известен как МГУА[4]. Определены следующие основные критерии селекции моделей:

-                   критерий регулярности (точности);

-                   критерий несмещённости (поведение модели проверяется на разных обучающих выборках).

Однако процедуры, лежащие в основе МГУА, изначально исходят из принципа изоляции исследователя (эксперта) от процесса селекции моделей. В частности нет механизма, который позволял бы учитывать начальные представления исследователя о структуре модели, что затрудняет интерпретацию полученных исследователем результатов.

В противоположность МГУА методы анализа данных предоставляют исследователю свободу в выборе методов, в основе которых лежат различные эмпирические гипотезы[5] о структуре модели идентификации. Но как отмечалось выше, эти методы не располагают достаточным набором критериев, подтверждающих значимость полученных результатов.

Таким образом, совместное использование подходов, отражённых МГУА и в методах анализа данных позволит исследователю воспользоваться сильными сторонами обоих подходов.

Общая задача идентификации может быть сформулирована с использованием принципиальной схемы[6] на рис.1. Пусть в результате каких-либо экспериментов (преобразований) над некоторым объектом получены его признаки (входное воздействие модели идентификации)  и известна его принадлежность к некоторому образу (отклик модели идентификации) . Требуется определить вид (структуру) и параметры некоторой модели F, ставящей в соответствие  и .

 

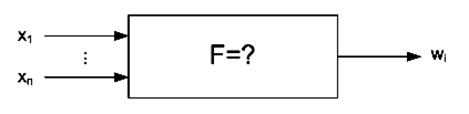
Рис. 1. Принципиальная схема задачи идентификации.

 

В работе радиограмма конкретного индивидуума представлена в виде матрицы распределения интенсивности излучения E, которая: в строках содержит значения интенсивности излучения для различных частотных интервалов; в столбцах содержит значения интенсивности излучения для различных моментов времени. В данной работе рассматриваются процессы с частотами от 1/120 с^-1 до 1/2 с^-1, моменты времени от 1 до 600 с.

 

Частотно-временной образ, в виде матрицы E, позволяет рассматривать исходную реализацию, как набор реализаций (строки матрицы) случайных процессов, в общем случае нестационарных, определённых частотными характеристиками исходной реализации.

Далее каждой матрице E {(t_0i;t_1i)} ставится в соответствие вектор признаков. Элемент вектора признаков – усреднённое значение интенсивности излучения на пересечении выбранного частотного интервала (f_0i;f_1i) и набора временных {(t_0i;t_1i)} интервалов.

Пусть M – обучающая выборка, все элементы которой описываются векторами признаков. W – множество образов, к которым принадлежат элементы множества M. Принадлежность элемента обучающей выборки к конкретному образу определяется экспертом на основании анализа сопутствующей информации, которая собирается об объектах исследования на этапе регистрации радиограммы.

Сформулируем гипотезу об оптимальной структуре модели идентификации следующим образом: существуют такие множества временных и частотных интервалов {(t_0i;t_1i)}, {(f_0i;f_1i)}, на которых возможно формирование обучающих выборок M со следующими свойствами: M содержит компактные группы элементов (кластеры), причём существуют наиболее «информативные» множества временных и частотных интервалов {(t_0i;t_1i)}, {(f_0i;f_1i)}, для которых образованные компактные группы (кластеры) в большей степени соответствуют классам W.

Определим требования к алгоритмам вычисления критериев селекции модели, исходя из гипотезы об её структуре.

Сформулированная гипотеза определяет следующие требования к алгоритму вычисления критерия регулярности. На первом шаге работы алгоритма на основе анализа обучающей выборки должны быть выделены кластеры. На втором шаге должна быть получена количественная оценка степени соответствия полученного разбиения классам W.

Критерий непротиворечивости требует проверки адекватности модели на различных выборках. Мерой адекватности модели является критерий регулярности. Таким образом, вычислительная процедура критерия непротиворечивости формирует набор значений критерия регулярности и формирует доверительный интервал для каждой модели.

Окончательный выбор модели должен производиться на основании совместного рассмотрения критерия регулярности и критерия непротиворечивости.

Критерий регулярности

Рассмотрим алгоритм вычисления критерия регулярности.

Пусть W содержит k образов. Произведём разбиение элементов обучающей выборки методом k-средних на k кластеров. Получим подмножества элементов S_i, i=1,..,k.

На втором шаге алгоритма необходимо дать численную оценку полученным результатам. Рассмотрим процедуру вычисления критерия регулярности с позиции информативности[7] вектора признаков.

 Рассмотрим обучающую выборку M, как матрицу, строки которой образуют векторы признаков. Столбцы матрицы M, рассмотрим в качестве системы признаков M_desc индивидуумов. В соответствии с гипотезой о структуре эффективной модели получаем множество B={M_desc} различных систем признаков. Связь между множеством объектов обучающей выборки M и системой признаков из множества B (у нас для каждой системы признаков существует обучающая выборка) будем обозначать как M^b.

Если будет введена некоторая мера информативности, то конкретное её значение будет определяется:

·                    решающей функцией D;

·                    обучающей выборкой M^b;

·                    множеством распознаваемых образов .

Итак, пусть D – решающая функция, B – множество систем признаков, M^b– обучающая выборка. Среди B всех возможных систем признаков информативной считаем систему, которая при заданных W и D обеспечивает стоимость потерь, вызываемых ошибками распознавания, N, не превышающие определённого порога N₀. Необходимой (информативной) является система минимальной сложности (стоимости). Так что фактически на обучающих выборках M^b решается переборная задача типа

Решающая функция D должна обеспечить разбиение M^b на непересекающиеся подмножества S_i. Причём число таких подмножеств должно совпадать с числом образов в обучающей выборке W. Так как мы не располагаем решающими правилами в признаковом пространстве , то должны использовать методы без учителя. В данной работе используется метод k-средних.

Можно выделить два крайних результата применения решающей функции D к M^b, с точки зрения стоимости потерь:

·                    в идеальном случае должно установиться однозначное соответствие между принадлежностью каждого индивидуума к множеству S_i и образу из W. В этом случае стоимость потерь минимальна;

·                    либо мы получим примерно равное присутствие индивидуумов одного образа в каждом подмножестве S_i.. В этом случае стоимость потерь максимальная.

Введём меру ошибок распознавания на основании идеологии физической энтропии системы.

Пусть N-число строк матрицы M, N(W_j) – число строк в матрице M, которые относятся к образу W_j, N(W_j/S_i) – число строк, принадлежащих к образу W_j, но отнесённых решающей функцией D к подмножеству S_i.

Пусть

,                                                              (2)

На основании (2) введём меру стоимости потерь N для системы признаков  следующим образом:

N=                                                             (3)

Итак, выражение (3) и есть числовое значение критерия регулярности.

Критерий непротиворечивости

Рассмотрим алгоритм вычисления критерия непротиворечивости.

Основной идеей, лежащей в основе вычисления критерия непротиворечивости, является вычисление критерия регулярности на различных подмножествах обучающей выборки M и построение доверительных интервалов. Чем меньше доверительный интервал (меньше дисперсия критерия регулярности), тем менее противоречива модель идентификации.

Для получения доверительных интервалов использовался метод перекрёстной проверки[8]. Из обучающей выборки M поочерёдно исключалось по одному элементу. В работе число различных значений критерия регулярности варьировалось от 20 до 30. Для получения доверительного интервала использовалось предположение о нормальности распределения критерия регулярности.

Рассмотрим результаты решения задачи на примере следующих обучающих выборок: , , , где W_1,W₂ , W_{3 ,} W₄ , W₅ – различные образы.

Критерий регулярности вычислялся на различных частотных интервалах для каждой обучающей выборки. Всего в работе выделялось девять частотных интервалов.

На рисунках 2, 3, 4 представлены значения критерия регулярности и величины доверительных интервалов для обучающих выборок M₁, M₂, M₃ соответственно.

 

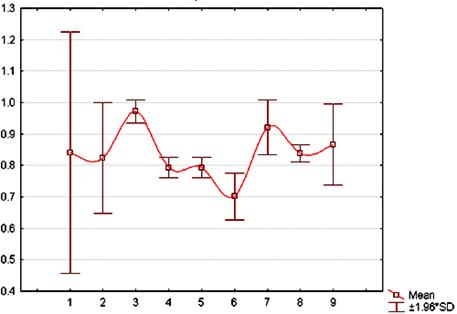
Рис. 2. Зависимость стоимости потерь от номера частотного окна для M_1.

 

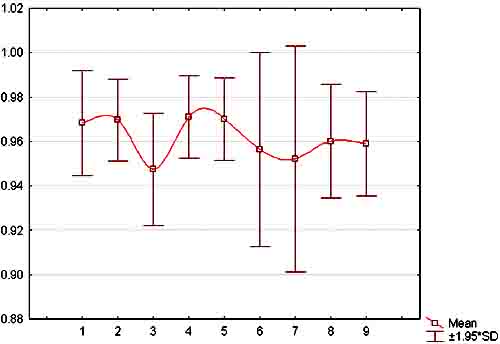
Рис. 3. Зависимость стоимости потерь от номера частотного окна для M_2.

 

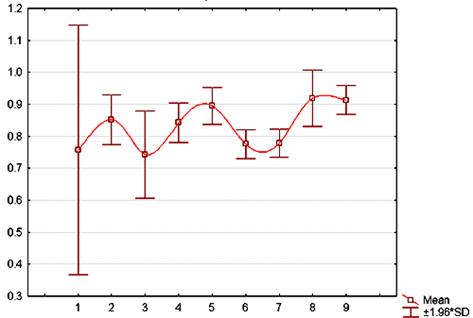
Рис. 4. Зависимость стоимости потерь от номера частотного окна для M_3.

 

Проведём интерпретацию результатов на примере обучающей выборки М₁ для частного интервала 4.

Воспользуемся аппаратом факторного анализа[9]. Матрица M представляется в виде произведения: M=AP, где A - матрица факторных нагрузок (коэффициентов регрессии факторов по признакам); P - матрица искомых факторов для отдельных индивидуумов. Причём здесь рассматриваются гипотетические факторы, объясняющие значимые корреляции между признаками.

На рисунке 5 показаны собственные значения корреляционной матрицы и объяснённые доли дисперсии факторов для M₁. Для извлечения факторов использовался метод главных компонент.

 

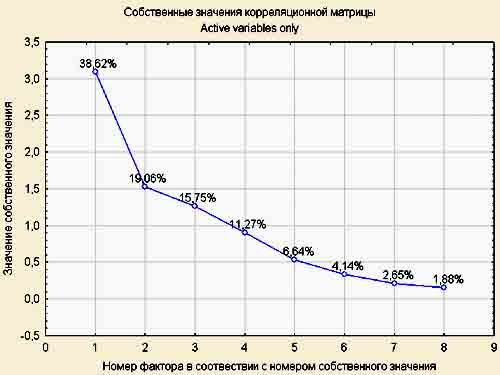
Рис. 5. Собственные значения корреляционной матрицы.

 

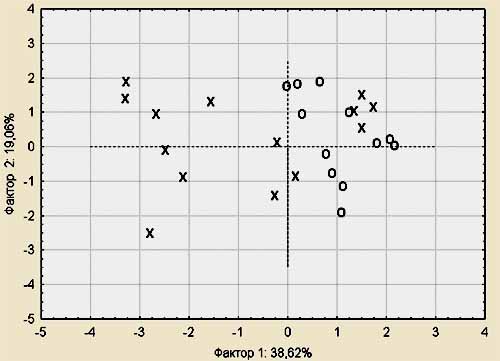
Рис. 6. Расположение индивидуумов в пространстве факторов.

 

Таблица 1.

Факторные нагрузки.

	Factor-1	Factor-2
K1_1	-0,827333	-0,065633
K1_2	-0,714971	-0,283698
K1_3	-0,699465	-0,045554
K1_4	-0,546823	-0,092817
K2_1	-0,552629	-0,319983
K2_2	-0,094724	-0,867966
K2_3	-0,714619	0,334521
K2_4	-0,529413	0,679522

 

Таблица 1 содержит значения факторных нагрузок. Видно, что первый фактор больше коррелирует с признаками, чем второй. Обратим внимание на рисунок 6. Видно, что образуются две компактные группы индивидуумов. Основной вклад в разделение компактных групп вносит первый фактор. Индивидуумы отмеченные «X» были отнесены экспертом к группе пациентов с состоянием здоровья «норма», индивидуумы отмеченные «O» были отнесены экспертом к группе пациентов с состоянием здоровья «артериальная гипертензия».

Рассмотрим факторную нагрузку более подробно. Признаки K1_1, K1_2, K1_3, K1_4 характеризуют реализацию случайного процесса первого канала. Признаки K2_1, K2_2, K2_3, K2_4 характеризуют реализацию случайного процесса второго канала. Признаки пронумерованы последовательно в соответствии с протеканием процесса во времени. На основании анализа факторных нагрузок можно сделать вывод о том, что с течением времени влияние первого фактора ослабевает.

МГУА обосновывает необходимость применения критериев селекции, предъявляет требования к этим критериям и способам и применения. Однако МГУА принципиально не предоставляет исследователю возможностей использования априорных сведений о структуре моделей идентификации.

Современные методы анализа данных позволяют исследователю формулировать свои представления о структуре модели идентификации в виде какой-либо эмпирической гипотезы. Преимущество такого подхода обычно выражается в простоте формулировок о структуре модели идентификации и в наличии готовых программ, который исследователь может использовать в своей работе. Однако основным недостатком методов, основанных на базовых эмпирических гипотезах, является отсутствие критериев оценки качества выбранной в процессе отбора модели.

 

Можно выделить следующие ключевые особенности подхода:

-                   Введение понятия гипотезы о структуре модели идентификации. Гипотеза о структуре модели идентификации основывается на так называемой базовой эмпирической гипотезе. Изначальная привязка к базовой гипотезе позволяет исследователю определить набор методов анализа данных, позволяет осуществить выбор программных комплексов анализа данных. В нашей работе в качестве базовой использовалась эмпирическая гипотеза компактности. В качестве метода анализа данных использовался метод кластерного анализа – метод k-средних. В работе использовался пакет статистического анализа Statistica 6.1.

-                   Последовательное применение и совместное рассмотрение критерия регулярности и критерия непротиворечивости. Одновременное отображение на графике оценок критерия регулярности и непротиворечивости даёт наглядный инструмент для принятия решения исследователем.

-                   Интерпретация результатов селекции моделей. Использование методов факторного анализа даёт возможность провести интерпретацию полученных результатов, с позиции построения общих факторов и определения весов отдельных признаков.

 

Литература.

 

1.                  Барсегян А.А., Куприянов М.С., Степаненко В.В., Холод И.И. Методы и модели анализа данных: OLAP и Data Mining. - СПб. : БХВ-Петербург, 2004. - стр. 336.

2.                  Гасилов В.Л., Кубланов В.С. Применение методологии вейвлет-анализа при функциональных исследованиях головного мозга // Биомедецинские технологии и радиоэлектроника. - 2001 r.. - 11. - стр. 14-20.

3.                  Гришин В.А., Камаев В.А. Математическое моделирование изделий и технологий. - Волгоград : ВолгПИ, 1986. - стр. 192.

4.                  Загоруйко Н.Г. Прикладные методы анализа данных и знаний. - Новосибирск : Ин-та математики, 1999. - стр. 270.

5.                  Иберла К. Факторный анализ / перев. В.М. Иванова. - М. : Статистика, 1980. - стр. 398. - Предисл. А.М. Дуброва.

6.                  Ивахненко А.Г., Юрачковскй Ю.П. Моделирование сложных систем по экспериментальным данным. – М. Радио и связь, 1987. – 120 с.

7.                  Форсайт Дэвид А., Понс Жан Компьютерное зрение. Современный подход. - М. : издательский дом «Вильямс», 2004. - стр. 928. - Пер. с англ.

 

Поступила в редакцию 03.09.2008 г.