Параметрические показатели
генерализованных мер информации
Кувырков
Петр Петрович,
кандидат технических наук, доцент,
Пензенская государственная технологическая
академия.
В данной работе в качестве одного из вариантов решения указанны проблемы измерения информации не только ее количества, но и качества непосредственно не требующего для этого знания вероятностей и соответственно статистической теории информации. Предлагаемые теоретические основы непосредственного измерения информации обеспечивают определение ее абсолютных, относительных нормализованных мер, учитывающих не только количественные, но и качественные ее особенности, характер изменения, симметрию, асимметрию функций отображающих ее сообщений, что определяет их актуальность и перспективность широкого использования.
Использование одного или нескольких информационных элементов, образующих собой некоторое целое, представим в качестве сообщения с вполне определённым его содержанием и характеризующим его количественно-качественными показателями.
Визуально данное сообщение 
представим образом
F(x), аналитически – математической
моделью f(x), а
параметрически – показателями информационности 
, информативности 
и информированности 
, с учётом того, что каждый элемент сообщения может
находиться в разных состояниях и взаимосвязей и взаимозависимостей с другими.
Обозначим через 
информационную j, 
– коммуникационную 
составляющие отдельно
взятого элемента сообщения .
Учитывая, что элемент сообщения может понимать одно из m состояний, определяемых основанием системы счисления или символами алфавита, его информационная составляющая будет определена этим состоянием:
, (1)
где 
.
Коммуникационная составляющая учитывает пространственное временное расположение элемента в сообщении и характеризуется его порядковым номером в этом сообщении:
, (2)
где 
Под информационностью отдельно взятого элемента сообщения 
будем понимать
генерализованную меру его информации 
, равную произведению информационной и коммуникационной его
составляющих
(3)
Таким образом, при определении информационности элемента в сообщении, измерении количества информации, учитывается не только содержательность данного элемента, но и его пространственно-временное расположение в сообщении.
Другими словами, исходя из сущности данного произведения, информационность отдельно взятого элемента определяет его информационный момент.
На рисунке 1 представлены графические изображения трёх сообщений.
Второй элемент, например, каждого из них характеризуется
информационностью, равной: 
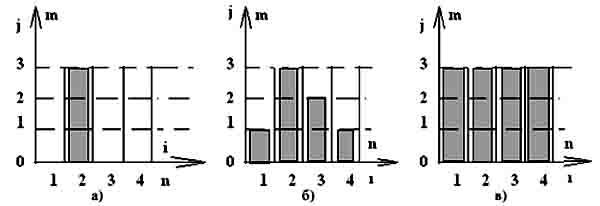
Рис. 1. Графическое представление сообщений:
Таким образом, информационность сообщения, а не отдельно взятого его элемента, будет определяться суммой информационностей всех входящих в его состав элементов
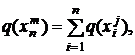(4)
где и j изменяются в следующих пределах:
, 
.
Учитывая сказанное, при n=4 и m=4 получим
Как следует, каждый последующий элемент сообщения увеличивает его информационность, а, следовательно, и количество присущей ему информации.
Максимальное значение информационности сообщения, будет при максимальном значении информационности каждого входящего в него элемента, то есть, при j = (m–1).
Например, для сообщения, изображенного графически на рисунке 1в, будем иметь
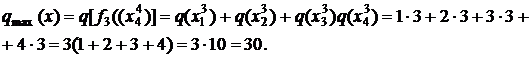
Характерной особенностью данных мер является то, что пространственно-временной фактор сообщения выражается суммой ряда чисел порядковых номеров или пространственно-временного расположения его элементов в сообщении. С изменением числа элементов в сообщении соответственно изменяется и величина его коммуникационности.
Обозначим через 
– коммуникационность
сообщения х.
Из рассмотрения сообщений, независимо от числа n входящего в каждое из них элементов, следует, что коммуникационность каждого из них, характеризуется закономерностью, определяемой законом комбинаторики – законом сочетаний
. (5)
В данном случае имеем
. (6)
При учёте информационности каждого элемента и его пространственно-временного расположения в сообщении, информационность сообщения примет максимальное значение, равное
(7)
Для сравнения в таблице 1 приведены значения максимальной информационности сообщений с разными значениями m и n.
Таблица 1.
Значения максимальной информационности сообщений 
.
|
m n |
|
|||
|
2 |
3 |
… |
m |
|
|
1 |
|
|
… |
|
|
2 |
|
|
… |
|
|
3 |
|
|
… |
|
|
4 |
|
|
… |
|
|
… |
… |
… |
… |
… |
|
n |
|
|
… |
|
Графическое изображение максимальной информационности 
сообщений, для разных
значений m и n , приведено на рисунке 2.
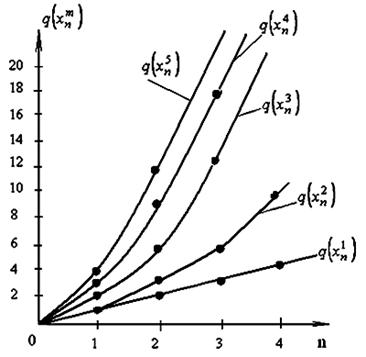
Рис. 2. Графическое
изображение максимальной информационности
m-ичных n-элементных
сообщений.
Кроме того, учитывая сказанное, в ряде случаев, кроме значения информационности сообщения, необходимо использовать и другие его параметрические показатели, к которым следует отнести, как было сказано выше, информативность и информированность.
Под информативностью будем понимать среднее значение информационности элементов сообщения, равное отношению его информационности к числу входящих в него элементов.
Обозначим 
– информативность сообщения
.
Тогда
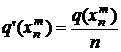. (8)
Другими словами, под информативностью будем понимать количество информации сообщения, приходящегося на один его элемент [1].
Под информированностью сообщения х будем понимать уровень его информационности по сравнению с максимально возможным ее значением для данного сообщения.
За данный показатель сообщения примем отношение информационности сообщения к информационности максимально возможной для него.
Обозначим 
– информированность
сообщения х.
Тогда
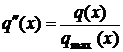. (9)
Подставляя в выражение (8) выражение (6), получим
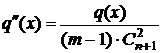(10)
Для сравнения информационности, информативности и информированности отдельно взятых сообщений, например, представленных двоичным трёхэлементным кодом, в таблице 2 приведены их расчётные значения.
Таблица 2.
Параметрические показатели двоичного трёхэлементного
кода.
|
i |
|
|
|
|
|
0 |
000 |
0 |
0 |
0 |
|
1 |
001 |
3 |
1 |
0,5 |
|
2 |
010 |
2 |
0,66 |
0,33 |
|
3 |
011 |
5 |
1,66 |
0,83 |
|
4 |
100 |
1 |
0,33 |
0,16 |
|
5 |
101 |
4 |
1,33 |
0,66 |
|
6 |
110 |
3 |
1 |
0,5 |
|
7 |
111 |
6 |
2 |
1 |
Как видно из таблицы 2, информированность сообщений изменяется в
диапазоне от 0 до 1, что характеризует уровень их информационной обеспеченности,
или информационной загруженности по сравнению с максимально возможной его
информационности.
Вывод. Востребованность нестатистического пути развития информации и ее теоретических основ из-за присущих им сложности, трудности и необходимости для измерения количества информации, определения и знании вероятностей, является предпосылкой поиска новых путей ее развития и совершенствования.
Литература.
1. Peter P. Kuvyrkov аnd Sergei K. Nаidenov, Generаl аspects of the аdvаncement of theory аnd prасtices of
informаtion systems,
ISSN 0368-492X, Volume 36 Number 1, 2007.
Поступила в редакцию 17.09.2008 г.