Методика оптимального распределения ресурсов центров обработки данных в Интернет

 

Тутова Наталья Владимировна,

аспирант Московского технического университета связи и информатики.

Научный руководитель – кандидат технических наук, профессор кафедры информационных технологий в экономике и управлении

Ворожцов Анатолий Сергеевич.

 

Современный этап развития глобальной сети Интернет характеризуется трансформацией традиционных услуг и бизнес-процессов компаний в электронные, основанные на Web-технологиях. Появились различные системы электронного бизнеса, такие как электронная торговля, он-лайн бронирование, электронные биржи и др., которые стали ключевыми в успехе работы компаний и поддержке их конкурентноспособности. Направление, связанное с развитием электронного бизнеса, является составной частью принятой в 2002 году комплексной федеральной целевой программы «Электронная Россия (2002-2010 годы.)». Крупные операторы связи, а также различные сервис-провайдеры стали предоставлять услуги хостинга приложений электронного бизнеса в собственных центрах обработки данных (ЦОД) [1].

Существуют различные виды хостинга. В случае выделенного хостинга (dedicated hosting) под каждое приложение отведена совокупность серверов, которые обслуживают только это приложение. Такой тип хостинга используется для работы крупных приложений, где кластер или несколько кластеров серверов обслуживает одно приложение. В случае совместного (shared) хостинга, кластер серверов обслуживает большое количество приложений и число приложений, как правило, превышает число серверов в кластере.

Современный процесс предоставления услуг сервис-провайдером характеризуется появлением соглашений о качестве обслуживания (SLA), гарантирующих со стороны сервис-провайдера определенный уровень качества. Наиболее распространенными показателями качества, оговариваемыми в SLA, являются среднее время ответа на запросы пользователей, максимальное время ответа для заданной доли запросов, коэффициент готовности, максимальное время простоя и др. Невыполнение SLA-соглашений сервис-провайдером может привести к значительным штрафам и потерям клиентов.

Наиболее распространенной архитектурой ЦОД в электронном бизнесе является многозвенная архитектура, при которой запросы пользователей обрабатываются различными кластерами серверов: Web-серверов, серверов приложений и серверов баз данных. Качество работы систем электронного бизнеса во многом зависит от того, насколько эффективно сервис-провайдер организует работу этих систем и управляет ресурсами ЦОД. Нагрузка к приложениям электронного бизнеса значительно меняется в течение суток, а также может иметь кратковременные всплески, при этом в периоды пиковых нагрузок интенсивность может превосходить среднее значение в несколько раз.

Управление ресурсами ЦОД направлено на обеспечение определенного в SLA-соглашениях качества обслуживания. Это может достигаться различными средствами, в том числе за счет оптимального распределения ресурсов между различными приложениями в ЦОД. Данной проблеме в зависимости от вида хостинга посвящено ряд работ [2-6], в которых поставлены однокритериальные задачи оптимизации с различной глубиной проработки. Критериями оптимизации в этих задачах являются затраты, доходы от SLA-соглашений, пропускная способность и др. При этом в каждой задаче вид SLA-соглашений строго определен, тогда как на практике возможны различные варианты задания SLA-соглашений. Поэтому предлагается методика оптимального распределения ресурсов ЦОД с учетом нескольких критериев, которая может использоваться для различных видов SLA-соглашений с различными видами хостинга.

Методика оптимального распределения ресурсов ЦОД и состоит из нескольких этапов [1].

1. На первом этапе проводится анализ SLA-соглашений. Выделяются четыре основных способа задания требований на качество обслуживания в SLA-соглашениях:

·                     Без выделения уровней обслуживания и классов запросов.

·                     С выделением уровней обслуживания, без выделения классов запросов.

·                     Без выделения уровней обслуживания, но с выделением классов запросов.

·                     С выделением уровней обслуживания и выделением классов запросов.

В первом случае в SLA-соглашении компании с сервис-провайдером рассматривается общий класс запросов, для которого задается пороговое значение среднего времени ответа. В случае если значение среднего времени ответа не превышает порогового значения, то компания платит сервис-провайдеру определенную величину вознаграждения, если среднее время ответа превышает пороговое значение, то сервис-провайдер выплачивает штраф компании. Под вознаграждением понимается плата сервис-провайдеру за оказанные услуги с заданным качеством обслуживания.

В случае выделения уровней обслуживания, задается несколько пороговых значений среднего времени ответа, при достижении которых изменяется величина вознаграждений и штрафов. Такой вид SLA-соглашений представляется в виде ступенчатой функции полезности [6], приведенной на рис. 1.

 

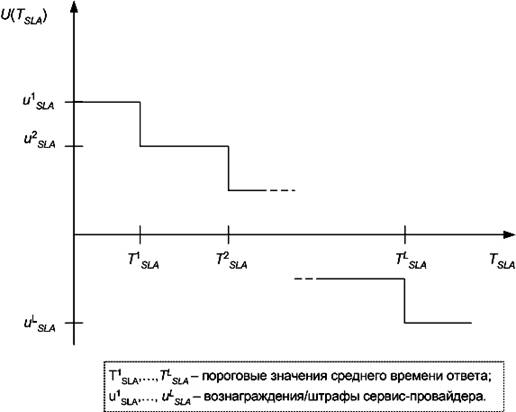
Рис. 1.

Ступенчатая функция полезности.

 

Способы задания ограничений на качество обслуживания для двух оставшихся видов SLA-соглашений аналогичны рассмотренным, только значения на качество обсушивание задается для нескольких классов запросов.

В случае если в SLA-соглашениях оговариваются классы запросов, то осуществляется переход к третьему этапу, где определяется оптимальное число серверов с учетом классов запросов.

Если в SLA-соглашениях не выделяются классы запросов, то для каждого SLA-соглашения строятся ступенчатые функции полезности (рис. 1). После этого строится агрегированная ступенчатая функция полезности для всех SLA-соглашений. Поскольку работа с прерывистой ступенчатой функцией является сложной, то предлагается аппроксимировать ступенчатую функцию полезности гладкой дифференцируемой функцией. Для удобства подбора функциональных зависимостей вместо единой функции полезности предлагается рассматривать функции вознаграждений (F_В) и штрафов (F_Ш) и аппроксимировать их экспоненциальной и степенной функциями соответственно:

;            ,                                                   (1)

где  t_SLA —среднее время ответа на запрос в системе;

a₁, b₁—коэффициенты функции вознаграждений по SLA-соглашениям;

a₂, b₂—коэффициенты функции штрафов по SLA-соглашениям.

В SLA-соглашениях не оговариваются затраты сервис-провайдера на обеспечение требуемого уровня среднего времени ответа. Поэтому для нахождения оптимального среднего времени ответа по SLA-соглашениям целесообразно также рассматривать функцию затрат от среднего времени ответа (F_З).

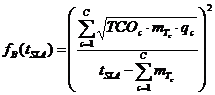,                                                                                    (2)

где  t_SLA —среднее время ответа на запрос в системе;

ТСО_с — совокупная стоимость владения сервером кластера c, ;

m_Tс — среднее время ответа на запрос сервером кластера с, ;

q_с — номинальная загрузка кластера с при заданной нагрузке λ_с, .

Математическая постановка задачи нахождения оптимального среднего времени ответа по SLA-соглашениям имеет следующий вид:

,                                                                                        (3)

при ограничениях

,                                                                                                         (4)

где 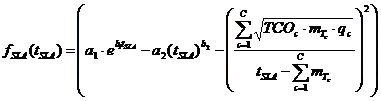 — функция прибыли от SLA-соглашений;

 —минимальное возможное среднее время ответа на запрос;

—максимальное возможное среднее время ответа на запрос.

Полученное среднее время ответа является ограничением на втором этапе оптимизации, где определяется оптимальное число серверов без учета классов запросов.

2. На втором этапе методики определяется оптимальное число серверов без учета классов запросов по критериям совокупной стоимости владения серверами ЦОД и пропускной способности. Постановка двухкритериальной задачи оптимизации выглядит следующим образом:

 F_ПС (S₁,…, S_C) =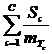,                                                                                   (5)

 F_TCO (S₁,…, S_C) = 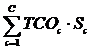;                                                                      (6)

при ограничениях

,                                                                                                 (7)

q_с< S_с ≤ S_с^max, с = 1, …, С,                                                                                                (8)

где   С—число кластеров в ЦОД;

S_с — число серверов в кластере с, ;

F_ПС(S₁,…, S_C)— критерий пропускной способности;

F_TCO(S₁,…, S_C)— критерий совокупной стоимости владения серверами ЦОД;

TCO_с—совокупная стоимость владения одним сервером кластера с, .

—среднее число посещений кластера с запросом за время его нахождения в системе;

q_с — номинальная загрузка кластера с с одним сервером при заданной нагрузке λ_с, ;

S_с^max — максимальное возможное число серверов в кластере с, ;

m_Tс — среднее время ответа на запрос сервером кластера с, ;

t^*_SLA — оптимальное среднее время ответа, определяемое из анализа SLA-соглашений.

Для ограничения на максимальное время ответа для заданной доли всех запросов, постановка задачи выглядит следующим образом:

 F_ПС(S₁,…, S_C) =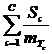,                                                                                    (9)

 F_TCO(S₁,…, S_C) = 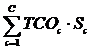;                                                                    (10)

при ограничениях

P[T ≥ V] ≤ ε,                                                                                                                   (11)

q_с< S_с ≤ S_с^max, .                                                                                                 (12)

3. На третьем этапе методики оптимизации находится оптимальное число серверов для случая, когда в SLA-соглашениях оговаривается среднее время ответа на запрос и/или максимальное время ответа для заданной доли всех запросов с делением этих запросов на классы.

Для ограничения на среднее время ответа на запрос, постановка задачи выглядит следующим образом:

 F_ПС(S₁,…, S_C) =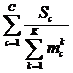;                                                                           (13)

 F_TCO(S₁,…, S_C) = 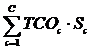;                                                                    (14)

при ограничениях

,    k = 1, . . . , K,                                                                             (15)

q_с< S_с ≤ S_с^max,               с = 1, …, С.                                                                               (16)

где  С—число кластеров ЦОД;

S_с — число серверов в кластере с, ;

F_ПС(S₁,…, S_C) — критерий пропускной способности;

F_TCO(S₁,…, S_C) — критерий совокупной стоимости владения;

TCO_с—совокупная стоимость владения одним сервером кластера с, ;

q_с — номинальная загрузка кластера с с одним сервером при заданной нагрузке λ_с, ;

 — среднее время ответа на запрос класса k сервером кластера с, ;

—среднее число посещений кластера с запросом класса k за время его нахождения в системе;

 —среднее время ответа на запрос класса k, задаваемое в SLA-соглашении;

S_с^max — максимальное возможное число серверов в кластере с, ;

Для ограничения на максимальное время ответа для заданной доли всех запросов, постановка задачи выглядит следующим образом:

 F_ПС(S₁,…, S_C) =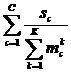;                                                                            (17)

 F_TCO(S₁,…, S_C) = 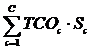;                                                                    (18)

при ограничениях

P[T^k > V^k] ≤ ε^k,            k = 1, . . . , K,                                                                             (19)

q_с< S_с ≤ S_с^max,               с = 1, …, С.                                                                               (20)

Возможны случаи, когда в SLA-соглашениях задаются оба ограничения на среднее время ответа и на максимальное время ответа для заданной доли запросов, тогда постановка задачи имеет вид:

 F_ПС(S₁,…, S_C) =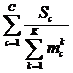;                                                                           (21)

 F_TCO(S₁,…, S_C) = 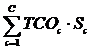;                                                                    (22)

при ограничениях

,    k = 1, . . . , K,                                                                             (23)

P[T^k > V^k] ≤ ε^k,            k = 1, . . . , K,                                                                             (24)

q_с< S_с ≤ S_с^max,               с = 1, …, С.                                                                               (25)

Ограничение (23) является ограничением на среднее время ответа, а (24)—ограничением на максимальное время ответа для заданной доли запросов.

Преложенная методика может быть включена сервис-провайдером в контур управления ресурсами ЦОД. При этом план распределения ресурсов ЦОД должен составляться при изменениях нагрузки, при внесении изменений в систему соглашений, а также состав приложений, например, добавлении нового приложения. Поэтому время решения задач имеет большое значение. В качестве метода решения многокритериальных задач предлагается использовать метод последовательных уступок с модифицированной процедурой определения компромиссной уступки, что позволит использовать методику оптимизации в контуре управления ресурсами ЦОД [7]. Указанная модификация реализована на С++. В качестве метода решения нелинейных задач оптимизации использовался модуль с открытым исходным кодом Cobyla, в котором реализован метод линейной аппроксимации М. Пауэлла [8].

Предлагаемая методика оптимального распределения ресурсов ЦОД позволит сервис-провайдеру, оказывающему услуги хостинга приложений электронного бизнеса с различными видами SLA-соглашений, находить оптимальное число серверов в кластерах, и тем самым выполнять свои обязательства по обеспечению качества обслуживания.

 

Литература.

 

1.                  Тутова Н.В., Ворожцов А.С. Модели оптимизации технологий обработки данных в сетях электронного бизнеса // «Труды Московского технического университета связи и информатики». – М.: «ИД Медиа Паблишер». – 2007. – С. 249 - 254.

2.                  Ranjan, S., Rolia, J., Fu, H., and Knightly, E. QoS-Driven Server Migration for Internet Data Centers. In Proceedings of the Tenth International Workshop on Quality of Service, Miami, FL (2002).

3.                  Pacifici G., Spreitzer M., Tantawi A., Youssef A., Performance Management for Cluster Based Web Services, IBM TJ Watson Research Center, TechReport, May 13, 2003

4.                  Zhang L., Ardagna D., SLA Based Profit Optimization in Web Systems, — 13^th International Conference on World Wide Web (WWW’04), New York, USA, 2004. — pp. 462-463.

5.                  Urgaonkar B., Dynamic Resource Management in Internet hosting Platforms, Ph.D., University of Massachusetts Amherst, 2005.

6.                  Liu Z., Squillante M.S., Wolf J.L., Optimal Control of Resource Allocation in e-Business Environments with Strict Quality-of-Service Performance Guarantees,  Proceedings of the 41st IEEE Conference on Decision and Control, 2002, pp. 4431- 4439 vol.4.

7.                  Ворожцов А.С., Тутова Н.В. Оптимизация ресурсов центров обработки данных в сетях электронного бизнеса // «Труды Московского технического университета связи и информатики». Том 1. – М.: «ИД Медиа Паблишер». – 2008. – С. 133 - 136.

8.                  Powell M.J.D.. A view of algorithms for optimization without derivatives. Department of Applied Mathematics and Theoretical Physics, Cambridge, 2007.

 

Поступила в редакцию 23.09.2008 г.