Цифровой широкополосный преобразователь Гильберта звуковых сигналов

 

Харитонов Владимир Борисович,

профессор, кандидат технических наук,

Зирова Юлия Константиновна,

аспирант кафедры звукотехники,

ведущий специалист отдела перспективных разработок ООО «Технощит СПб».

Санкт-Петербургский государственный университет кино и телевидения.

 

Для выполнения многих функций обработки звуковых сигналов полезен аналитический сигнал. Он состоит из вещественной и мнимой частей, сопряженных по Гильберту. Это означает, что все составляющие частотных спектров этих двух сигналов имеют фазы, различающиеся на . Для получе­ния пары сопряженных по Гильберту сигналов необходимо пропустить исходный сигнал через фазовраща­тель (преобразователь Гильберта).

Согласно теории модуляционных преобразований звуковых сигналов [1], если дополнить исходный сигнал сопряженным по Гильберту, то появится возможность управлять огибающей звукового сигнала, т. е. вмешиваться в процессы атаки и затухания звука или видоизменять динамические характеристики переда­ваемого сигнала. При обработке сигналов по их модулирующим функциям выделяют огибающую (ампли­тудную модулирующую функцию) и/или мгновенную частоту (частотную модулирующую функцию) сиг­нала, преобразовывают либо одну из модулирующих функций, либо обе и синтезируют измененный желае­мым образом сигнал. Безынерционное преобразование динамического диапазона – одна из возможностей практического применения теории модуляционного анализа-синтеза [2]. При этом выделяют огибающую сигнала, воздействуют на нее с целью создания требуемого вида преобразования (лимитирования, компрес­сирования, экспандирования, шумоподавления) и синтезируют сигнал по обработанной амплитудной модулирующей функции.

В аналоговой аппаратуре модуляционного анализа-синтеза для выделения модулирующих функций использу­ется широкополосный фазовращатель, состоящий из соединенных последовательно фазовра­щающих звеньев, построенных на операционных усилителях. Фазовращатель является одним из ключевых звеньев устройства модуляционного анализа-синтеза, поскольку качество звука после синтеза сигнала во многом зависит от его точности. Отклонение ФЧХ фазовращателя от требуемой приводит к искажениям огибающей и к паразитной амплитудной модуляции при синтезе сигнала, что создает нелинейные искаже­ния. Аналоговый фазовращатель не в состоянии обеспечить высокую точность ФЧХ из-за отклонения пара­метров элементов аналоговой схемы от требуемых значений, их температурной и временной нестабильно­сти. Цифровой преобразователь Гильберта свободен от недостатков аналоговой реализации. Единственная проблема в цифровой реализации может быть связана с конечной разрядностью вычислений. Но в настоя­щее время устройства цифровой обработки сигналов поддерживают широкий диапазон форматов представ­ления чисел, кроме того, есть способы борьбы с эффектами квантования, что дает возможность снизить влияние конечной разрядности до допустимо малого уровня.

Для выделения амплитуды и фазы произвольного сигнала  необходимо создать на его основе аналитический сигнал

                                                                                                   (1)

Вещественная часть аналитического сигнала совпадает с исходным сигналом . Мнимая часть  называется сопряженным сигналом или квадратурным дополнением. Сопряженный сигнал получается из исходного с помощью преобразования Гильберта. Вычисляется преобразование Гильберта следующим образом:

Данный интеграл представляет собой свертку сигнала  и функции . Это означает, что преобразова­ние Гильберта может быть выполнено линейной системой с постоянными параметрами.

Частотная передаточная функция преобразователем Гильберта определяется следующим образом:

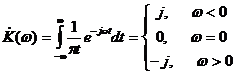
АЧХ преобразователя Гильберта равна единице всюду, кроме нулевой частоты, то есть преобразование Гильберта не меняет амплитудных соотношений в спектре сигнала, лишь удаляя из него постоянную со­ставляющую. Фазы всех спектральных составляющих в области положительных частот изменяются на ­–90º, в области отрицательных частот – изменяются на 90º.

Таким образом, устройство, осуществляющее преобразование Гильберта должно представлять собой иде­альный фазовращатель, вносящий на всех частотах фазовый сдвиг, равный ±90º.

Представив (1) в показательной форме, можно определить огибающую и мгновенную фазу сигнала

,

где -огибающая

и - мгновенная фаза

 

Дискретное преобразование Гильберта можно получить в результате дискретизации аналогового сигнала (1). Тогда вещественный сигнал  можно представить в комплексной форме

,

,

,

где  – номер отсчета;

 и  - n-отсчеты вещественной и мнимой частей аналитического сигналы,

 - огибающая сигнала , вычисляемая, как следует из приведенных равенств, по формуле

,

- мгновенная фаза

,

производную от мгновенной фазы называют мгновенной частотой

Так же как и в аналоговом варианте, цифровые сигналы, фазы всех составляющих частотного спектра которых отличаются на , называют сопря­женными по Гильберту, а устройство формирования пары сопряженных сигналов – цифровым преоб­разователем Гильберта (ЦПГ).

 

Для достижения высокого качества безынерционного преобразования динамического диапазона звуковых сигналов на основе модулирующих функций ЦПГ должен в широкой полосе частот, от 32 Гц до 16 000 кГц, обеспечивать частотно-независимый фазовый сдвиг сигнала на  с погрешностью порядка  градуса. Величина фазовой погрешности выбирается такой, чтобы возникающие из-за нее пульсации мгновенной амплитуды тонального сигнала не были заметны на слух. При такой фазовой погрешности их уровень не превысит -80 дБ.

 

ЦПГ можно построить с помощью быстрого преобразования Фурье (БПФ) или на основе цифрового фильтра. Использование БПФ дает выигрыш с точки зрения вычислительных затрат, но для достижения высокого качества синтеза ЦПГ на паре БПФ необходимо решить ряд проблем: выбор весовой функции, окна анализа и метода перекрытия. Построение ЦПГ на основе цифрового фильтра уступает по вычислительным затратам, но гарантирует расчет точных характеристик преобразователя для определенного порядка фильтра без решения дополнительных проблем.

Возможны варианты построения реального ЦПГ в виде как рекурсивного (БИХ), так и нерекурсивного (КИХ) фильтра. Вариант на КИХ-фильтрах, обладающих строго линейной фазочастотной характеристикой, позволил бы с высокой точностью получить требуемый фазовый сдвиг, но амплитудно-частотная характеристика таких фильтров неравномерная. Синтез ЦПГ на основе КИХ-фильтра путем минимаксной аппроксимации АЧХ при неравномерности ±0,1% приводит к практически неприменимым результатам: для воспроизведения АЧХ с за­данной точностью требуется фильтр двухтысяного порядка. Для обеспечения работы устройства в ре­жиме реального времени ЦПГ 2000-го порядка не пригоден, так как требует выполнения 2 тыс. умножений для вычисления каждого отсчета выходного сигнала.

Рекурсивный ЦПГ можно реализовать на основе фазовых звеньев. Известны аналоговые широкополосные фазовращающие цепи, которые состоят из фазовых звеньев первого или второго порядка, сгруппированных в две параллельные цепи. Передаточная функция фазового звена первого порядка:

,

а его фазовая характеристика:

Для фазового звена второго порядка указанные функции имеют вид

 

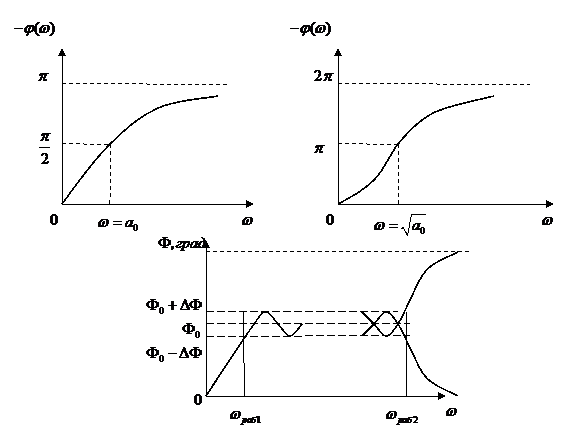
Рис.1. Фазовые характеристики фазовых звеньев первого (слева), второго (справа) порядков и возможные частотные зависимости фазоразностных характеристик (снизу).

 

АЧХ таких звеньев горизонтальная, а ФЧХ неравномерная. Путем включения нескольких звеньев в параллельные цепи и подбором их параметров можно добиться в довольно широком частотном диапазоне воспроизведения требуемой ФЧХ с необходимой точностью. Графики фазовых характеристик для фазовых звеньев первого и второго порядка, а также возможные частотные зависимости фазовых характеристик широкополосных фазовращающих цепей представлены на рис. 1. Конструирование передаточной характеристики ЦПГ из фазовых звеньев второго порядка дает больше степеней свободы, поскольку появляется возможность варьировать не только значения частот, а еще и добротности звеньев. Но в этом случае усложнятся вычисления фазоразностной характеристики, т. к. функция арктангенса определена в диапазоне от  до  и превышения этих значений будут приво­дить к скачкам фазы. Появится необходимость отслеживать эти моменты и бороться с ними, что усложняет вычислительный алгоритм. С учетом этого для реализации ЦПГ были выбраны звенья 1-го порядка.

Для синтеза передаточной функции цифрового фазовращателя 1-го порядка удобно применить метод билинейного z-преобразования [3], который позволяет решить эту задачу, выполнив элементарные преобразования передаточной функции аналогового фильтра-прототипа. Получаемая методом билинейного z-преобразования передаточная функция  цифрового фазового звена первого порядка равна:

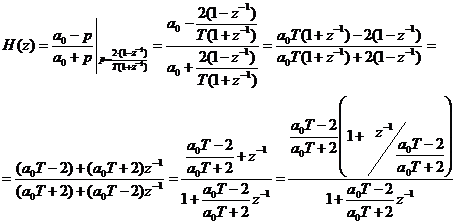
где  – параметр передаточной функции;

 – соотношение между комплексными переменными p и z.

Равенство на всех частотах единице АЧХ, полученной в результате билинейного преобразования, сохраняется:

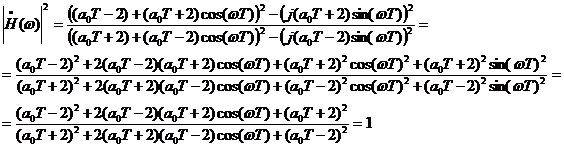
Билинейное Z-преобразование обеспечивает однозначное отображение p-плоскости на z-плоскость, однако из-за существенной деформации верхней части шкалы частот при пересчете аналоговых частот фильтра в цифровые, нельзя воспользоваться уже готовыми табличными значениями рассчитанных полюсов и нулей для аналоговых фазовращателей [4]. В связи с этим была сформулирована и решена задача синтеза рекурсивного ЦПГ.

 

Решение задачи расчета рекурсивного ЦПГ сводится к нахождению коэффициентов его передаточной функции, обеспечивающих аппроксимацию фазоразностной характеристики в том или ином смысле (например, в среднеквадрати­ческом или минимаксном) при условиях:

§                    - частота дискретизации;

§                    - заданная фазоразностная характеристика;

§                    - допустимая погрешность воспроизведения фазоразностной характеристики;

§                    - граничная частота левой полосы задерживания;

§                    - граничная частота правой полосы задерживания.

Обозначив аппроксимируемую фазоразностную характеристику через , где  – дискрет­ный ряд частот, на которых вычисляются отклонения получаемой и заданной характеристик фильтра,  – коэффициенты ЦПГ, квадрат суммарной ошибки на всех частотах можно представить следующим образом:

                                                                           (2)

где ,

где k – номер варианта вектора коэффициентов;

- k–вариант вектора искомых коэффициентов.

Поиск наилучшего вектора коэффициентов можно рассматривать как оптимизационную задачу с целевой функцией E(k). Целью оптимизации является, как и обычно, получение минимального значения целевой функции. Выбор минимизации по критерию среднеквадратической ошибки обусловлен тем, что она связана с меньшими вычислительными затратами [5].

В этом случае выражение для вычисления целевой функции можно представить следующим образом:

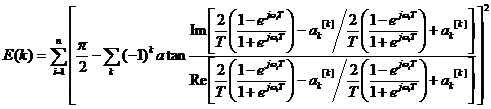       (3)

Программная реализация алгоритма минимизации квадрата ошибки (3) средствами компьютерной программы Matlab для двух звеньев дает результат, превышающий допустимую величину примерно в 1000 раз. Чем больше используется звеньев при заданном диапазоне частот, тем меньшую погрешность преобразования может обеспечить преобразователь Гильберта. Добавление двух звеньев уменьшит ошибку аппроксимации примерно вдвое. Нарастив число звеньев до четырнадцати, получаем требуемый результат (рис. 2).

 

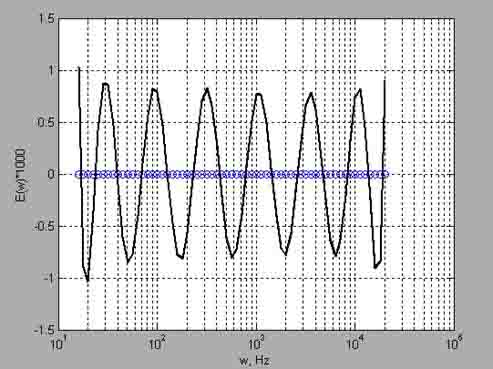
Рис.2. Функция ошибки аппроксимации ЦПГ 14-го порядка.

 

Максимум ошибки аппроксимации ЦПГ 14-го порядка не превышает значения 0,001, что соответствует допустимому отклонению фазоразностной характеристики от  на .

В таблице 1 представлены полученные в результате решения оптимизационной задачи значения коэффициентов ЦПГ 14-го порядка:

 

Таблица 1.

Параметры передаточных звеньев

широкополосного преобразователя Гильберта звуковых сигналов.

Номер звена	Параметры звеньев, уменьшенные в 1.0e+004 раз
1–3	0.00048518675766	0.00163055965752	0.00335740918799
4-6	0.00626782752705	0.01137283355493	0.02044462431750
7-9	0.03662898355173	0.06553963618113	0.11726697123668
10-12	0.21029737978017	0.38039733560797	0.70786036902878
13-14	1.45355676743930	4.87721714033418

 

Расчеты велись при повышенной в 4 раза, до 176 400 Гц, частоте дискретизации. Четырехкратная передискретизация связана с тем, что при исходной частоте дискретизации (44 100 Гц) и верхней граничной частоте ЦПГ 19 200 Гц часть полюсов цифровых фазовращателей 1–го порядка не могут быть реализованы, так как они находятся выше предела, устанавливаемого теоремой Котельникова (половина частоты дискретизации). Только четырехкратная передискретизация позволила получить заданную точность фазочастотной характеристики, причем последняя имела в рабочей полосе необходимое число колебаний (15) относительно номинального значения.

С учетом вышеизложенного перед Гильбертовским фильтром необходимо добавить элемент, который увеличит частоту дискретизации в четыре раза. Такой элемент состоит из экспандера частоты дискретизации (ЭЧД) и фильтра-интерполятора, выполняющего последующую обработку сигнала с выходной частотой дискретизации. ЭЧД, увеличивающий частоту дискретизации в m раз, представляет собой блок, который преобразует входной сигнал с частотой дискретизации  в выходной сигнал с частотой дискретизации, равной  добавляя m–1 нулевых отсчетов к каждому исходному. При этом спектр в полосе частот от нуля до  остается прежним. Это означает, что он имеет периодический характер, причем период соответствует первоначальной частоте дискретизации 44 100 Гц. Наряду с передискретизацией, на фильтр можно возложить функцию ограничения полосы частот входного сигнала таким образом, чтобы она соответствовала полосе рабочих частот преобразователя Гильберта. Это означает, что фильтр-передискретизатор подавляет периоды спектра, кратные прежней частоте дискретизации, и оставляет только периоды, соответствующие новой частоте дискретизации. Наряду с подавлением периодов спектра, соответствующих первоначальной частоте дискретизации, на фильтр-интерполятор возлагается функция ограничения полосы частот обрабатываемого сигнала снизу и сверху и формирования рабочей полосы фильтра Гильберта. В этом случае составляющие входного сигнала, для которых фазовая разность имеет большую погрешность, окажутся достаточно ослабленными. Во временной области применение фильтра-интерполятора означает вычисление дополнительных 3 отсчетов между имеющимися в исходном сигнале вместо нулевых отсчетов, созданных ЭЧД.

В таблице 2 представлены коэффициенты фильтра-интерполятора, рассчитанного в программе Matlab по аналоговому прототипу фильтра Кауэра методом билинейного Z–преобразования при условиях:

§                    – частота дискретизации;

§                    – граничная частота левой полосы задерживания;

§                    – граничная частота левой полосы пропускания;

§                    – граничная частота правой полосы пропускания;

§                    – граничная частота правой полосы задерживания;

§                    – максимально допустимое отклонение в полосе пропускания.

 

Таблица 2.

Параметры звеньев фильтра-интерполятора 10-го порядка,

составленного из каскадного включения пяти звеньев 2-го порядка.

N звена	Параметры звеньев второго порядка
1	-1.80619588659576	0.81927182859481	1.0	-0.45197100491919	1.0
2	-1.83283881254658	0.86679514572762	1.0	-1.68625051264239	1.0
3	-1.86457715287801	0.92260492108346	1.0	-1.83756375330890	1.0
4	-1.88887225352307	0.96313415417392	1.0	-1.87757656530070	1.0
5	-1.90743227701583	0.98936448378843	1.0	-1.88990634363506	1.0

 

Таким образом, средствами точной цифровой обработки сигналов возможно построение высокоточного широкополосного преобразователя Гильберта звуковых сигналов на основе цифрового фильтра.

Анализ известных методов синтеза цифровых фильтров показывает, что практическая реализация ЦПГ на основе фазовых звеньев оптимальна по сложности и вычислительным затратам.

Разработанный преобразователь Гильберта звуковых сигналов обеспечивает высокое качество получаемого аналитического сигнала и таким образом может быть использован для реализации многих операций обработки звука, в том числе для построения цифровых устройств модуляционного анализа-синтеза.

 

Литература.

 

1.                  Основы модуляционных преобразований звуковых сигналов/Ю.М. Ишуткин, В.К. Уваров; Под ред. В.К. Уварова: Монография. – СПб.: СПбГУКиТ, 2004.

2.                  Применение модуляционных преобразований звуковых сигналов: Монография/ В.К Уваров, В.М. Плющев, М.А. Чесноков; Под ред. В.К Уварова – СПб.: СПбГУКиТ, 2004.

3.                  Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. -М.:Мир, 1978.

4.                  Справочник по расчету и проектированию ARC-схем / Букашкин С. А., Власов В. П., Змий Б. Ф. и др.; Под ред. А. А. Ланнэ. – М.: Радио и связь, 1984.

5.                  Мэтьюз, Джон, Г., Финк, Куртис, Д. Численные методы. Использование MATLAB. –М.: Издательский дом «Вильямс», 2001.

 

Поступила в редакцию 03.09.2008 г.