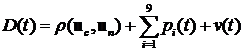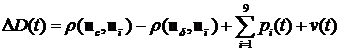Исследование алгоритмов предварительной обработки данных траекторных измерений методами имитационного моделирования

 

Стубарев Денис Викторович,

аспирант Сибирского государственного ордена Трудового Красного Знамени научно-исследовательского института метрологии,

руководитель структурного подразделения ООО «ФБ Консалт».

 

Целью работы является проведение анализа имеющихся методов и средств предварительной обработки результатов траекторных измерений, подбор алгоритма оптимального оценивания данных на этапе первичной обработки информации и составление рекомендаций по его использованию для получения результата, максимально приближенного к реальному.

В данной работе предварительная обработка проводилась с помощью робастных алгоритмов фильтрации, которые нечувствительны к выбросам в данных, обеспечивают гладкое восполнение пропущенных данных и позволяют идентифицировать скачки фазовой неоднозначности в фазовых измерениях.

 

Основу координатно-временных определений, выполняемых по сигналам спутниковых навигационных систем ГЛОНАСС и GPS, составляют результаты текущих измерений наклонных дальностей от навигационных спутников (НС) до антенны приемной аппаратуры (траекторных измерений). Такие измерения производятся сетью беззапросных измерительных станций (БИС) для целей восстановления орбит НС и последующего формирования эфемеридно-временного обеспечения ГЛОНАСС, или комплектом приемной аппаратуры при решении геодезических и навигационных задач по сигналам радиовидимой орбитальной группировки НС [1].

Существует ряд задач, в которых отбрасывать ошибочные измерения нельзя. К таким задачам относятся: синхронизация разнесенных в пространстве часов (такие часы, входят в состав беззапросных измерительных станций (БИС), которые используются для уточнения (ЭВО), управление разнесенными в пространстве объектами. И задачи, обеспечивающие функционирование самих спутниковых навигационных систем (СНС).

 

Поверка счетчиков тепла

обслуживание приборов учета тепла. Низкие цены

ekstralab.ru

Исходным материалом для решения задач определения координат тела в околоземном и наземном пространстве являются результаты высокоточных измерений наклонных геометрических дальностей от навигационного спутника (НС) до измерительной станции.

Уравнение для геометрической дальности:

,                                        (1)

где  – геометрическая наклонная дальность;

 – вектор текущих координат НС (,,), определенный в системе координат ЕГСК;

 – вектор текущих координат потребителя (,,), определенный системе координат ЕГСК.

Начало единой геоцентрической системы координат (ЕГСК) - в центре масс Земли. Ось Ze направлена в сторону Северного полюса и проходит через Международное условное начало (МУН) 1900-1905 г.г. Ось Xe проходит через гринвичский меридиан, соответствующий МУН, а ось Ye дополняет систему до правой. Эта система координат вращается вместе с Землёй [1].

Измерение указанных наклонных дальностей радиотехническими методами сводится к определению длительности интервала времени, необходимого для прохождения навигационного сигнала от НС до приемной антенны потребителя. Этот измеренный временной интервал , выраженный в единицах длины и именуемый в дальнейшем псевдодальностью, связан с геометрической наклонной дальностью (1) уравнением измерений:

,                                                                   (2)

где  – псевдодальность. Измеренный интервал времени прохождения навигационного сигнала от НС до БИС, выраженный в единицах длины;

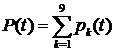 – группа факторов, влияющих на точность измерений;

 – возмущения стохастической природы, не поддающиеся компенсации.

Согласно [1], ошибочными являются примерно 15% всех измерений, а в городских условиях до 30%.

Существует несколько источников ошибок измерений и источников ошибок определения интересующих параметров. Эти источники ошибок, в уравнении (2) представлены в виде факторов, влияющих на точность измерений. Принято разделять их на источники ошибок, вызванные работой аппаратуры, на источники ошибок, связанные с влиянием внешней среды и влиянием ошибок исходных данных, то есть в данном случае, с ошибками координат спутников [1].

Большую часть факторов, влияющих на точность траекторных измерений, можно скомпенсировать на основе применения известных математических моделей для этих поправок. Частично параметры этих согласующих моделей содержатся в составе навигационного сообщения (для каждого НС передаются поправки на уходы бортовых часов, для GPS – параметры модели ионосферной задержки) и могут быть измерены (метеопараметры для расчета тропосферной задержки) [4].

Однако остаются факторы, не поддающиеся компенсации.

Проведенный анализ, что наиболее существенными факторами, искажающими результаты траекторных измерений, являются (Рисунок 1):

-                   выбросы, образующиеся, в результатах псевдодальномерных измерений, в результате многопутности. То есть когда сигнал от НС отражается от различных объектов (дома, деревья, конструкции,…). На рисунке 1.б, выбросы показаны на отчетах 102 и 134, на рисунке 1.а. выбросы не указаны в связи с их малым размером;

-                   разрывы в данных, образующиеся в результате удаления пачки выбросов, или при потере синхронизации. В этом случае для исключения разрыва применяется метод гладкого восполнения данных. На рисунке 1, разрыв в данных показан на интервале отчетов 298-349;

-                   для фазовых измерений, скачки фазы, образующиеся в результате потери синхронизации и возобновление последующих измерений. Чтобы сохранить возможность использования фазовых измерений необходимо этот скачек идентифицировать (определить момент возникновения скачка и его амплитуду) и ввести соответствующую компенсирующую поправку в фазовые измерения.

Перечисленные обстоятельства приводят к необходимости проведения предварительной обработки результатов траекторных измерений с целью:

-                   исключения выбросов из состава данных и замена их значениями удовлетворяющих условиям гладкости траектории, для кодовых измерений;

-                   гладкого восполнения пропущенных данных при потерях синхронизации;

-                   оценивания и компенсации скачков фазовой неоднозначности в фазовых измерениях.

Для этой цели автором разработаны и применяются рекуррентные процедуры (на основе рекуррентных процедур оптимальной фильтрации калмановского типа), адаптирующиеся к измерительной информации.

Поскольку погрешности измерений наклонной дальности и выбросы в результатах измерений, возникающие вследствие многопутности, малы  по сравнению с самими дальностями  (Рисунок 1.а), для обработки измерений следует ввести в рассмотрение опорную траекторию достаточно близкую к реальной траектории спутника, и анализировать относительное движение НС [2].

В работе предлагается в качестве опорной траектории использовать траекторию полученную с помощью эфемерид поступающих по каждому НС в составе навигационного сигнала и последующего гладкого восполнения функции с помощью полиномов Чебышева по методике изложенной в [4]. При этом и отсутствие данных  в моменты нарушения синхронизации для  также будут трактоваться как выбросы или пачка выбросов.

 

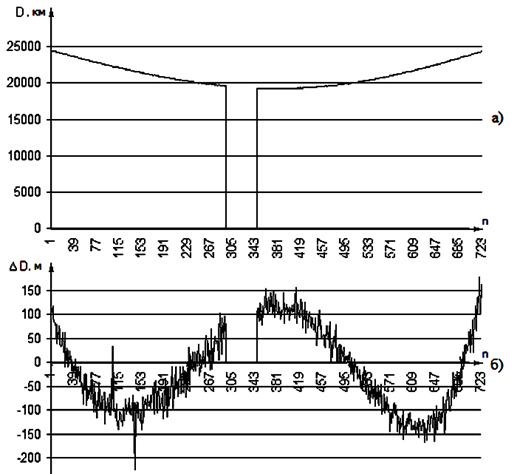
Рис. 1. Изменение дальности а) абсолютное  и б) относительно опорной траектории .

 

На рисунке 1 на горизонтальной оси представлены отчеты с интервалом в 30 секунд.

Возможность расчета опорной траектории движения спутника, позволяет рассчитать функцию опорной дальности . В дальнейшем, в работе, будут рассматриваться относительные дальности , т.е. разности между измеренной текущей дальностью до спутника  и расчетной дальностью  (Рисунок 1.б).

Расчетная дальность  получена с помощью программного имитатора, при действии в канале измерения помехи с СКО=10 м.

Для перехода к относительным дальностям добавляем в обе части уравнения (2) расчетную дальность:

,                                           (3)

где  – текущие координаты спутника на опорной траектории, полученные расчетным путем.

Вопросам выявления и исключения аномальных значений посвящено большое количество работ (см. например обзоры [3, 5]), однако в них практически не содержится конструктивных рекомендаций по применению конкретных методов в рассматриваемых случаях.

Ключевой задачей данной работы является сравнительный анализ ряда подходов к обнаружению аномальных наблюдений и уменьшению их влияния на результат измерений, а также выбор наиболее приемлемых статистических процедур для практики обнаружения сомнительных наблюдений в измеренных данных.

Следуя [3, 5], наиболее приемлемыми являются два подхода к обнаружению выбросов в результатах наблюдений:

-                   подход, основанный на линейной теории оценивания с использованием адаптивной рекуррентной процедуры калмановской фильтрации;

-                   использование робастных процедур и медианной фильтрации.

Метод оценивания состояния динамических систем с использованием фильтра Калмана (ФК) получил широкое распространение в практике статистической обработки траекторных измерений. Это объясняется тем, что алгоритм калмановской фильтрации имеет рекуррентную форму, удобную для реализации на ЭВМ, и обеспечивает определение оценок с минимальными дисперсиями среди всех линейных оценок.

Уравнение фильтра Калмана:

,                                                                                 (4)

где ;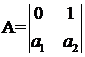

 – вектор оценок навигационных параметров спутника;

H – единичная матрица ;

K – матрица коэффициентов алгоритма оценивания;

 – подготовленный вектор радионавигационных параметров, полученный путем разности относительных дальностей , и суммы компенсирующих поправок : .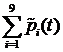

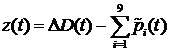При использовании данного метода, вычисление оценки выполняется с опорой на предыдущее значение, и в случае появления в выборке аномального значения, соответствующая ему оценка несет за собой ошибку и в следующие вычисления, существенно снижая эффективность фильтрации.

Именно поэтому использование алгоритма калмановской фильтрации в чистом виде не приносит ожидаемых результатов. Для исключения подобного эффекта необходимо заведомо исключить из выборки аномальные значения, и только после этого использовать вышеизложенную процедуру. Другими словами, перед использованием процедуры калмановской фильтрации, есть необходимость в ее адаптации, под случай присутствия выбросов.

Для устранения данной проблемы введем доверительный интервал:

,                                                                          (5)

где σ – значение дисперсии.

Все значения, попадающие в указанный промежуток, будем считать достоверными, а те, которые не попали – исключать, для этого в уравнении (4) обнуляем матрицу K, и в качестве оценки используется сам прогноз.

В случае прихода пачки выбросов ошибка фильтрации, связанная с обнулением матрицы К накапливается, с каждым новым выбросом уводя оценку все дальше и дальше за доверительный интервал (Рисунок 2).

 

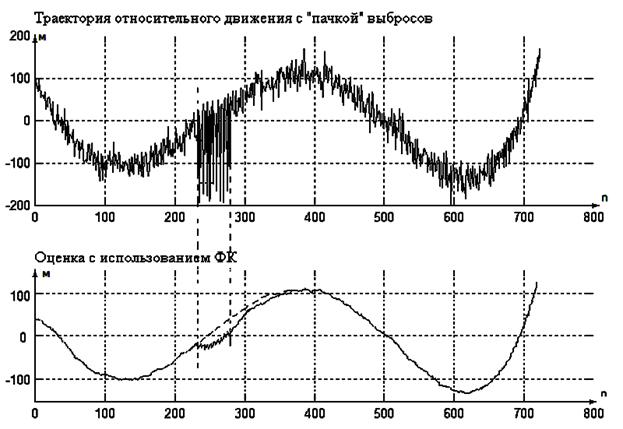
Рис. 2. Использование ФК в условиях действия пачки выбросов.

 

Таким образом, можно прийти к выводу, что перед использованием адаптивной процедуры калмановской фильтрации желательно произвести проверку измерений на наличие аномальных значений, и по возможности произвести исключение пачек выбросов.

Именно поэтому наиболее подходящим, в условиях действия выбросов, является способ робастного оценивания параметров траекторных измерений.

В статистике под робастностью понимают нечувствительность к различным отклонениям и неоднородностям в выборке, связанным с теми или иными, в общем случае неизвестными, причинами [3].

К семейству робастных оценок относится медиана. Метод фильтрации, основанный на использовании этой статистики, называется медианной [3].

Медианная фильтрация осуществляется посредством движения некоторой скользящей полосы, содержащей в себе нечетное количество точек (апертуры) вдоль последовательности измерений и замены значения элемента выборки в центре апертуры медианой исходных значений отсчетов, принадлежащих рассматриваемому интервалу. После применения медианного фильтра, получается более гладкая (по сравнению с исходной) результирующая последовательность измерений.

Основным преимуществом медианных фильтров над линейными фильтрами является эффективность при борьбе с импульсными шумами, к классу которых можно отнести и выбросы, но они хуже фильтруют шумы измерений.

В связи с вышеописанным, рассмотрим еще одну схему редактирования данных с неправдоподобными значениями, использующую свойство робастности медианы. Она называется процедурой «Тьюки 53Х». При вычислении оценки с помощью «Тьюки 53Х» усреднение по медиане используется дважды.

Анализ показал, что процедура «Тьюки 53Х» лучше справляется с шумами измерений.

Для проведения сравнительного анализа оценивания параметров НС по загрязненной выборке был выбран метод имитационного моделирования.

Термин «имитационное» определяет в моделировании такую область, которая относится к получению экспериментальной информации о сложном объекте, которая не может быть получена иным путем, как экспериментируя с его моделью на ПЭВМ.

Имитационное моделирование – это воспроизведение на ЭВМ (имитация) процесса функционирования исследуемой системы, соблюдая логическую и временную последовательность протекания процессов, что позволяет узнать данные о состоянии системы или отдельных ее элементов в определенные моменты времени.

Объектом моделирования является траектория движения НС.

Для проведения эксперимента используется программный имитатор ModBis24 [2], разработанный во ФГУП «СНИИМ», при непосредственном участии автора. С помощью данного программного обеспечения моделируется полет НС, и результатом работы программы является массив измеренных дальностей.

Последующая обработка измерений с целью получения оценки координат НС производилась с помощью программного приложения к ModBis24 Flysatell, а также средств Excel.

Моделирование проводилось с использованием следующих данных:

-                   интервал радиовидимости КА - 5ч;

-                   СКА шума измерений 20 м;

-                   количество выбросов – 3;

-                   амплитуда выбросов – 180 м;

-                   моменты появления выбросов: k₁=100, k₂=300, k₃=500.

Также был рассмотрен случай действия пачки выбросов.

 

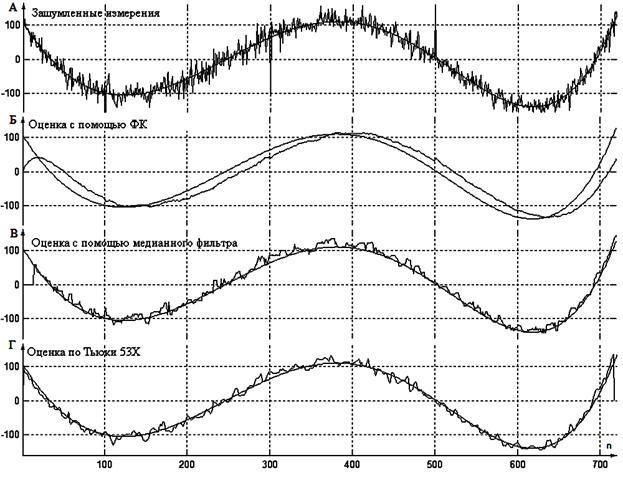
Рис. 3. Оценки измерений (1) с помощью ФК (2), МФ(3) и процедуры «Тьюки 53Х» (4).

 

Для анализа качества оценивания выборки измерений в условиях действия выбросов используем СКО, характеризующая степень наличия шумов в данных. Величины СКО при использовании различных процедур оценивания представлены в Таблица 1.

 

Таблица 1.

Величины СКО при использовании различных процедур оценивания.

Процедура оценки	СКО, м
Без использования фильтрации	20
Адаптивный фильтр Калмана	4.2
Медианный фильтр	11.7
Процедура Тьюки 53Х	9.4

 

Таким образом, из таблицы 1 видно, что помехи лучше отрабатывает адаптивный фильтр Калмана. Но использование его в чистом виде неоправданно из-за возможности появления в измерениях пачки выбросов (Рис. 2), тогда как фильтры, использующие свойство робастности медианы хорошо справляются с этой проблемой.

Исходя из вышесказанного, целесообразно применять процедуру «Тьюки 53Х» для исключения выбросов, а затем адаптивную фильтрацию Калмана для понижения уровня регулярных помех.

Таким образом, предварительная фильтрация данных с помощью процедуры «Тьюки 53Х» перед применением линейного фильтра Калмана позволяет добиться высокой точности оценивания результатов траекторных измерений (СКО = 2.3м), и избавиться от негативного влияния эффекта мультипути.

Программный имитатор измерительной информации сети беззапросной измерительной станции представляет собой эффективный инструмент для отработки эфемеридно-временного обеспечения космической навигационной системы ГЛОНАСС, позволяющий проводить сравнительный анализ алгоритмов оценивания орбит, определять рациональный состав измерений и осуществлять подбор согласующих моделей для расчета компенсирующих поправок к факторам, влияющим на точность измерений. Также имитатор ModBis24 позволил провести анализ имеющихся методов и средств предварительной обработки данных, и составить рекомендации по использованию того или иного алгоритма для получения результата, максимально приближенного к реальному.

 

В процессе проведения исследования алгоритмов предварительной обработки данных траекторных измерений, был сделан вывод о том, что для решения задачи, необходимо иметь такую опорную траекторию движения НС, которая была бы максимально приближена к истинной траектории. Было принято для этих целей использовать априорную эфемеридную информацию и опирающуюся на нее интерполяцию. Анализ показал, что лучше всего для этих целей подойдет интерполяция ортогональными полиномами Чебышева второго порядка.

Предложена адаптивная конструкция фильтра Калмана адаптирующаяся к поступающей информации, что сделало процедуру фильтрации робастной.

Произведенный сравнительный анализ подходов и алгоритмов выявления и исключения выбросов (использование адаптивного линейного фильтра Калмана, медианного фильтра и процедуры «Тьюки 53Х») показал целесообразность предварительной медианной фильтрации исходных данных перед применением линейного фильтра.

В фазовых измерениях, факт скачка обнаруживается по дифференцированной фазе. Тогда в производной скачек будет выглядеть как выброс. В эти моменты результаты фазовых измерений сравниваются с результатами таких же кодовых измерений.

Результаты исследований нашли применение в разработанном во ФГУП «СНИИМ» имитаторе измерительной информации получаемой с сети беззапросных измерительных станций по орбитальной группировке ГЛОНАСС.

Полученные результаты модельных исследований и результаты обработки реальных сигналов хорошо согласуются с теоретическими положениями, положенными в основу синтеза робастных алгоритмов обработки измерительной информации.

 

Литература.

 

1.                  Антонович К.М. Использование спутниковых радионавигационных систем в геодезии // Том 1. М.: ФГУП «Картгеоцентр», 2005. – 334 с.

2.                  Владимиров В.М., Гречкосеев А.К., Толстиков А.С. Имитатор измерительной информации для отработки эфемеридно-временного обеспечения космической навигационной системы ГЛОНАСС// Измерительная техника. – 2004.- 8. – С.12-14.

3.                  Ершов А.А. Стабильные методы оценки параметров //Автоматика и телемеханика, 1978, №8, с. 66-100.

4.                  Жданюк Б.Ф. Основы статистической обработки траекторных измерений // М.: Сов. радио, 1978.- 384с., ил.

Микешина Н.Г. Выявление и исключение аномальных значений //Заводская лаборатория, 1966, №3, с. 310-318.

 

Поступила в редакцию 15.09.2008 г.