УДК
621.755 - 251
Способ измерения динамического
дисбаланса жестких роторов в режиме малых угловых колебаний.
Кочкин
Сергей Вячеславович,
аспирант кафедры «Автоматика
и телемеханика»,
старший научный сотрудник ООО «НПП
«Техника», г. Пенза,
Кожевников Вячеслав Владимирович,
аспирант
кафедры «Металлообрабатывающие станки и комплексы»,
Пензенский Государственный Университет.
Аннотация.
В статье рассмотрено теоретическое обоснование возможности измерения динамического дисбаланса жестких роторов с двумя плоскостями приведения в режиме малых угловых колебаний. Составлены и решены дифференциальные уравнения движения.
На рисунке 1 показана схема установки балансируемого ротора в двух положениях в прямом, исходном положении а) и в обратном, перевернутом положении б).
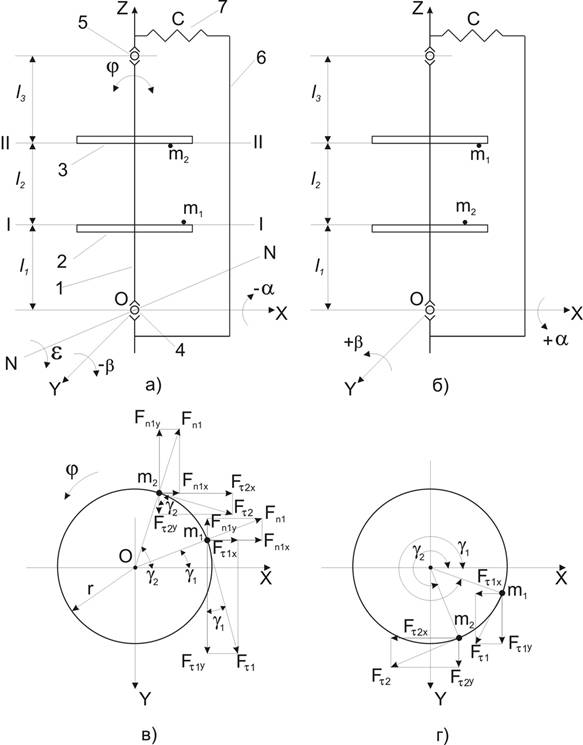
Рис. 1.
Схема установки ротора с избыточными
массами и неуравновешенными силами инерции.
Известно [1],
что в общем случае неуравновешенность ротора вызывается смещением главной центральной
оси инерции с геометрической оси ![]() и определяется центробежными
моментами инерции и величиной смещения центра масс ротора относительно оси
вращения. В этом случае неуравновешенность ротора может быть
сведена к двум избыточным массам
и определяется центробежными
моментами инерции и величиной смещения центра масс ротора относительно оси
вращения. В этом случае неуравновешенность ротора может быть
сведена к двум избыточным массам ![]() и
и ![]() , расположенным, как показано на рисунке 1, а) в двух плоскостях
приведения неуравновешенности I
и II на некотором
радиусе
, расположенным, как показано на рисунке 1, а) в двух плоскостях
приведения неуравновешенности I
и II на некотором
радиусе ![]() с двумя угловыми
коэффициентами
с двумя угловыми
коэффициентами ![]() и
и ![]() . На этом рисунке ротор изображен в виде вала 1 с насаженными
на него дисками 2 и 3. Они же являются плоскостями приведения неуравновешенности
I и II. Нижняя цапфа ротора опирается на
неподвижный шарнир 4, расположенный в центре О неподвижной системы
координатных осей X, Y, Z. Продольная ось ротора в неподвижном
состоянии совпадает с осью Z.
Верхняя цапфа ротора упирается в верхний шаровой шарнир 5, упруго связанный с
рамой 6 упругим элементом 7. Жесткость
. На этом рисунке ротор изображен в виде вала 1 с насаженными
на него дисками 2 и 3. Они же являются плоскостями приведения неуравновешенности
I и II. Нижняя цапфа ротора опирается на
неподвижный шарнир 4, расположенный в центре О неподвижной системы
координатных осей X, Y, Z. Продольная ось ротора в неподвижном
состоянии совпадает с осью Z.
Верхняя цапфа ротора упирается в верхний шаровой шарнир 5, упруго связанный с
рамой 6 упругим элементом 7. Жесткость ![]() этого элемента вместе
с экваториальным моментом инерции ротора
этого элемента вместе
с экваториальным моментом инерции ротора ![]() или
или ![]() определяют собственную
частоту системы ротор-рама
определяют собственную
частоту системы ротор-рама ![]() и характеризуют режим
вынужденных угловых колебаний ротора вокруг осей X или Y под действием неуравновешенных его сил инерции. Для тел
вращения
и характеризуют режим
вынужденных угловых колебаний ротора вокруг осей X или Y под действием неуравновешенных его сил инерции. Для тел
вращения ![]() .
.
На рисунке 1,
а и б показаны координаты расположения плоскостей приведения ![]() и
и
![]() причем
причем ![]() а их сумма равна общей
длине ротора
а их сумма равна общей
длине ротора ![]() .
.
Известно, что тангенциальные силы определяются угловым ускорением, а центробежные силы – квадратом угловой скорости.
Тогда при методе малых угловых колебаний имеем
![]() ,
,
![]()
Учитывая, что
амплитуда угловых колебаний весьма малая величина и принята в пределах
0,02…0,05 радиан, делаем вывод, что центробежные силы на один - два порядка
меньше тангенциальных и, следовательно, ими можно пренебречь. К тому же они
имеют двойную частоту ![]() и могут быть легко отфильтрованы
от основной частоты
и могут быть легко отфильтрованы
от основной частоты ![]() .
.
На рисунке 1, в и г показаны угловые координаты ![]() и
и ![]() избыточных масс
избыточных масс ![]() и
и ![]() соответственно в
исходном и перевернутом положениях ротора, а также неуравновешенные силы
инерции и их проекции на координатные оси X и Y.
При этом на рисунке 1, в показаны как
тангенциальные силы
соответственно в
исходном и перевернутом положениях ротора, а также неуравновешенные силы
инерции и их проекции на координатные оси X и Y.
При этом на рисунке 1, в показаны как
тангенциальные силы ![]() и
и ![]() и
их проекции, так и центробежные силы
и
их проекции, так и центробежные силы ![]() и
и ![]() и их проекции, а на
рисунке
и их проекции, а на
рисунке
Как видно из
рисунка, кроме задаваемых угловых колебаний ![]() под действием неуравновешенных
сил инерции возникают так же угловые колебания ротора
под действием неуравновешенных
сил инерции возникают так же угловые колебания ротора ![]() вокруг оси
вокруг оси ![]() , лежащей в плоскости координатных осей X и Y и проходящей через неподвижный центр О в направлении, перпендикулярном
суммарному вектору всех неуравновешенных сил инерции. Для нахождения этого
направления используется один поворотный датчик неуравновешенности,
расположенный в верхней горизонтальной плоскости рамы 6, по максимальному показанию которого определяется величина суммарного вектора
неуравновешенных сил инерции, а по его угловому положению – направление этого
вектора.
, лежащей в плоскости координатных осей X и Y и проходящей через неподвижный центр О в направлении, перпендикулярном
суммарному вектору всех неуравновешенных сил инерции. Для нахождения этого
направления используется один поворотный датчик неуравновешенности,
расположенный в верхней горизонтальной плоскости рамы 6, по максимальному показанию которого определяется величина суммарного вектора
неуравновешенных сил инерции, а по его угловому положению – направление этого
вектора.
В настоящей работе принят метод измерения неуравновешенности в проекциях на координатные оси X и Y.
Для этого
общее колебательное движение ![]() вокруг оси
вокруг оси ![]() раскладывается на два
движения:
раскладывается на два
движения: ![]() - вокруг оси X
под действием проекций неуравновешенных сил на ось Y и
- вокруг оси X
под действием проекций неуравновешенных сил на ось Y и ![]() - вокруг оси Y
под действием проекций неуравновешенных сил на ось X. При этом используются два неподвижных
датчика проекций неуравновешенности также расположенные в верхней
горизонтальной плоскости рамы в направлении осей X и Y.
- вокруг оси Y
под действием проекций неуравновешенных сил на ось X. При этом используются два неподвижных
датчика проекций неуравновешенности также расположенные в верхней
горизонтальной плоскости рамы в направлении осей X и Y.
Таким образом,
можно составить по два дифференциальных уравнения колебательных движений ![]() и
и ![]() вокруг осей X и Y соответственно для исходного (рисунок
1, а) и перевернутого положения
ротора (рисунок 1, б).
вокруг осей X и Y соответственно для исходного (рисунок
1, а) и перевернутого положения
ротора (рисунок 1, б).
В первом случае имеем
![]()
![]()
![]()
![]() ,
,
где
![]() - экваториальный
момент инерции относительно оси X
или Y;
- экваториальный
момент инерции относительно оси X
или Y;
![]() - коэффициент,
учитывающий сопротивление среды или демпфирования колебаний;
- коэффициент,
учитывающий сопротивление среды или демпфирования колебаний;
![]() - моментная жесткость
упругого элемента;
- моментная жесткость
упругого элемента;
![]() ,
, ![]() и
и ![]() ,
, ![]() - соответственно
угловые ускорения и угловые скорости угловых колебаний
- соответственно
угловые ускорения и угловые скорости угловых колебаний
![]() и
и ![]() .
.
Пренебрегая
величинами второго порядка малости (слагаемые с двойной частотой и с коэффициентом
![]() ) будем иметь:
) будем иметь:
![]()
![]()
Аналогично для второго случая (рисунок 1, б)
![]()
![]()
Поделив почленно каждое из этих уравнений на экваториальный момент
инерции ротора ![]() , приведем эти уравнения к следующему виду:
, приведем эти уравнения к следующему виду:
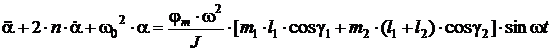 (1)
(1)
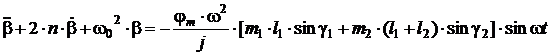 (2)
(2)
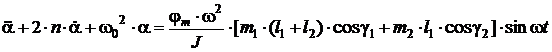 (3)
(3)
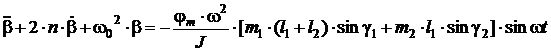 (4)
(4)
Здесь ![]() - коэффициент
затухания колебаний;
- коэффициент
затухания колебаний;
![]() - собственная частота
колебаний системы.
- собственная частота
колебаний системы.
Решение выполняем по известной методике, представляя, как сумму общего решения без правой части и частного решения с правой частью.
Для получения
периодического решения необходимо, чтобы удовлетворялось условие ![]() , что обычно имеет место на практике.
, что обычно имеет место на практике.
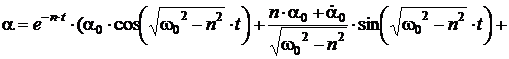
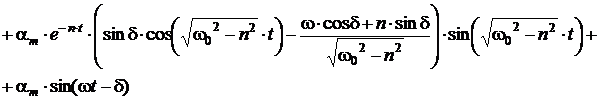
Аналогично: 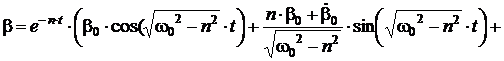
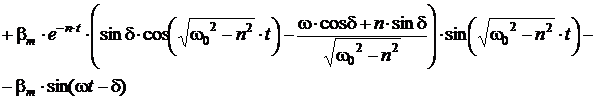
Первые
слагаемые в этих выражениях представляют затухающие свободные колебания,
вызванные начальным отклонением колебательной
системы от положения равновесия на величину ![]() и
и ![]() соответственно и сообщающие
ей начальные скорости
соответственно и сообщающие
ей начальные скорости ![]() и
и ![]() . Частота этих колебаний несколько меньше собственной
частоты. Это отличие составляет всего несколько процентов и может не
учитываться. Вторые слагаемые представляют затухающие колебания той же частоты,
что и свободные, и возникают из-за наличия возмущающих моментов. Наконец третьи
слагаемые - это вынужденные колебания, имеющие частоту возмущающих моментов от
неуравновешенных сил инерции, амплитуды которых
. Частота этих колебаний несколько меньше собственной
частоты. Это отличие составляет всего несколько процентов и может не
учитываться. Вторые слагаемые представляют затухающие колебания той же частоты,
что и свободные, и возникают из-за наличия возмущающих моментов. Наконец третьи
слагаемые - это вынужденные колебания, имеющие частоту возмущающих моментов от
неуравновешенных сил инерции, амплитуды которых ![]() и
и ![]() определяются по
формулам:
определяются по
формулам:
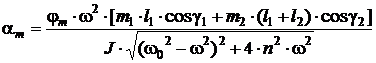 , (5)
, (5)
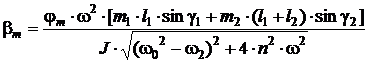 . (6)
. (6)
Фазовый сдвиг
этих колебаний ![]() равен
равен 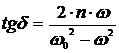 и может изменяться в
пределах от
и может изменяться в
пределах от ![]() до
до
![]() , в зависимости от соотношения частот собственных колебаний
, в зависимости от соотношения частот собственных колебаний ![]() и вынужденных
колебаний
и вынужденных
колебаний ![]() .
.
Применяя уравнения (5) и (6) можно определить величину и место расположения дисбаланса ротора при его измерениях в режиме малых угловых колебаний.
Литература.
1. Щепетильников В.П./Основы балансировочной
техники. М. - Машиностроение. 1975. С.527.
Поступила в редакцию 11.03.2008 г.