Фильтрация импульсных помех при параметрическом
оценивании случайных сигналов.
Сафронов
Станислав Владимирович,
аспирант
Санкт-Петербургского Государственного Электротехнического Университета (ЛЭТИ),
программист
ООО «ЭвоСквайр»,
Научный руководитель – доктор
технических наук
Авдеев
Борис Яковлевич.
В статье приведено описание нескольких методов
фильтрации импульсных помех при параметрическом оценивании случайных сигналов.
Рассмотрены их достоинства и недостатки. Проведен количественный анализ
характеристик рассмотренных методов.
При решении задач
статистического анализа и, в частности, при параметрическом оценивании случайных
сигналов проблема наличия в выборке аномальных измерений имеет достаточно
важное значение. Присутствие аномальных наблюдений может приводить к оценкам,
которые совершенно не согласуются с выборочными данными. Такими аномальными
измерениями могут быть импульсные помехи. Эти помехи являются случайными, кратковременными искажениями
параметров сигнала, и могут быть описаны формой импульса и функциями
распределения пиковой амплитуды и плотности. Для дискретных сигналов,
искаженных действием такого шума, отсутствует строгая, в математическом смысле,
постановка и решение задачи фильтрации, на данный момент известны некоторые
непараметрические алгоритмы, наиболее приемлемым из которых является алгоритм
медианной фильтрации [1].
Медианные фильтры достаточно часто применяются на практике, как средство предварительной обработки цифровых данных. Специфической особенностью и основным достоинством таких фильтров является слабая реакция на отсчеты, резко выделяющиеся на фоне соседних, что позволяет применять медианную фильтрацию для устранения аномальных значений в массивах данных. Характерной особенностью медианного фильтра является его нелинейность. Во многих случаях применение медианного фильтра оказывается более эффективным по сравнению с линейными фильтрами, поскольку процедуры линейной обработки данных являются оптимальными при гауссовом распределении помех, что не всегда характерно для реальных сигналов. В случаях, когда перепады значений сигналов велики по сравнению с дисперсией гауссовского шума, медианный фильтр дает меньшее значение среднеквадратической ошибки выходного сигнала в отношении к входному, незашумленному сигналу при сравнении с оптимальными линейными фильтрами [2].
Медианный фильтр представляет собой оконный фильтр, последовательно скользящий по массиву сигнала, и возвращающий на каждом шаге один из элементов, попавших в окно (апертуру) фильтра. Выходной сигнал yk скользящего медианного фильтра шириной n для текущего отсчета k формируется из входного временного ряда …, xk-1, xk, xk+1,… в соответствии с формулой:
yk = Me(xk-(n-1)/2,…, xk,…,xk+(n-1)/2),
где Me(x1,…,xn) = x((n+1)/2) – элементы вариационного ряда, т.е. ранжированные в порядке возрастания значений x1 = min(x1,…, xn) ≤ x(2) ≤ x(3) ≤ … ≤ xn = max(x1,…, xn). Ширина медианного фильтра выбирается с учетом того, что он способен подавить импульс шириной (n-1)/2 отсчетов, при условии, что n – нечетное число.
Таким образом, медианная фильтрация реализуется в виде процедуры локальной обработки отсчетов в скользящем окне, которое включает определенное число отсчетов сигнала. Для каждого положения окна выделенные в нем отсчеты ранжируются по возрастанию или убыванию значений. Средний по своему положению отсчет в ранжированном списке называется медианой рассматриваемой группы отсчетов, если число отсчетов нечетно. Этим отсчетом заменяется центральный отсчет в окне для обрабатываемого сигнала. При четном количестве отсчетов медиана устанавливается, как среднее арифметическое двух средних отсчетов. В качестве начальных и конечных условий фильтрации обычно принимается текущее значение сигнала, либо медиана находится только для тех точек, которые вписываются в пределы апертуры.
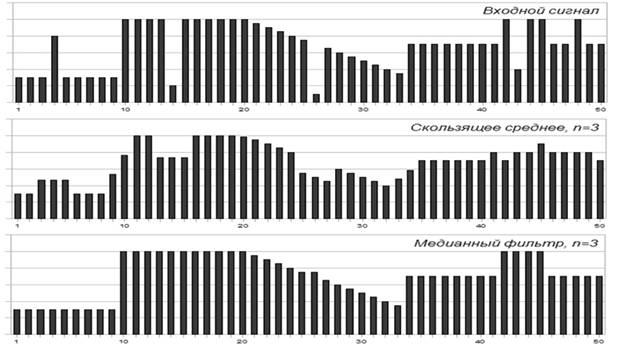
Рис. 1.
Благодаря свои характеристикам, медианные фильтры при оптимально выбранной апертуре могут сохранять без искажений резкие границы объектов, подавляя некоррелированные и слабо коррелированные помехи и малоразмерные детали. В аналогичных условиях алгоритмы линейной фильтрации неизбежно «смазывают» резкие границы и контуры объектов. На рис. 1 приведен пример обработки сигнала с импульсными шумами медианным фильтром и простым скользящим средним с одинаковыми размерами окна n = 3. Преимущество медианного фильтра здесь очевидно.
Таким образом, медианные фильтры обладают двумя основными достоинствами: хорошее подавление импульсных помех шириной менее половины окна фильтра и пропускание без искажений ступенчатых и пилообразных сигналов при малом размере окна. В тоже время у таких фильтров есть существенный недостаток — меньшая эффективность подавления гауссовского шума, чем у линейных фильтров.
Тем не менее, существует ряд способов, использование которых может уменьшить основной недостаток метода медианной фильтрации. Примером такого способа может быть применение медианной фильтрации с адаптивным изменением размера окна фильтра в зависимости от нестационарности сигнала и характера шумов (адаптивная медианная фильтрация)[3].
Как уже отмечалось, медианная фильтрация является нелинейной операцией над входным сигналом, которая наряду с исключением импульсных помех изменяет и статистические параметры сигнала, что может быть нежелательным для последующей обработки. Так как медианный фильтр является частным случаем рангового фильтра, то для определения влияния на статистические свойства сигнала необходимо найти закон распределения (n+1)/2 ранговой статистики, по следующей формуле [4]:
![]() ,
,
где: F(x) -
функция распределения входного сигнала, f(x)
- функция плотности вероятности входного сигнала, ![]() - функция плотности вероятности выходного сигнала, n — размер окна фильтра, i = (n+1)/2.
- функция плотности вероятности выходного сигнала, n — размер окна фильтра, i = (n+1)/2.
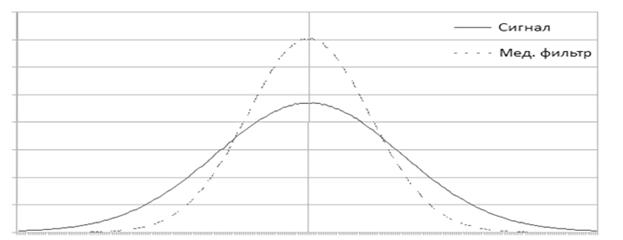
Рис. 2.
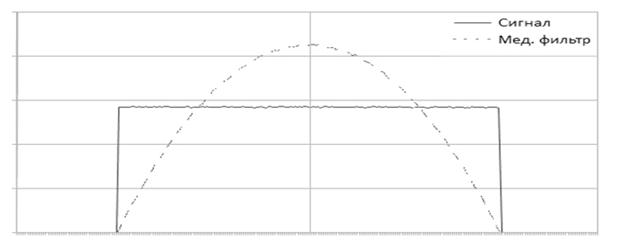
Рис. 3.
На рис. 2 приведен пример результата медианной фильтрации сигнала с гауссовым распределениями при ширине окна фильтра n=3 и исходный сигнал, а на рис.3 — c равномерным распределением. Как следует из этих графиков, при фильтрации происходит подавление преимущественно сигналов с большими отклонениями отсчетов от среднего значения с уменьшением среднеквадратического отклонения распределения, т.е. происходит сильное изменение статистических параметров сигнала.
Для фильтрации импульсных помех достаточно часто используется и другой распространенный алгоритм – простое скользящее среднее. Основным достоинством этого алгоритма является простота аппаратной и программной реализации. По всем остальным параметрам он существенно уступает медианной фильтрации импульсных помех. Стоит отметить и тот факт, что метод простого скользящего среднего имеет еще более сильное влияние на распределение статистических шумов и плохо подавляет высокочастотные составляющие шума, что говорит о его неэффективности для решения задачи импульсного сглаживания.
Таким образом, после рассмотрения двух распространенных методов фильтрации импульсных помех, можно сделать вывод, что при параметрическом оценивании случайных сигналов необходимо использовать метод, обладающий достоинствами медианного фильтра и не изменяющего статистические свойства остальной части сигнала, т.е. необходима сильная реакция фильтра на аномальные отсчеты, но при этом остальные отсчеты должны пропускаться без изменений.
В общем, задача фильтрации импульсных помех может
рассматриваться как обнаружение импульсного выброса с последующим исправлением
искаженных значений амплитуды принимаемого сигнала. Задача обнаружения обычно
формулируется в виде решающего правила, γ в
соответствии с которым принимается решение о наличии (γ =1) или отсутствии (γ = 0)
импульсной помехи в заданный момент времени наблюдения сигнала [5].
Таким правилом может служить метод исключения промахов [6]. В соответствии с этим правилом вычисляется оценка среднеквадратического отклонения результата измерения по n предыдущим измерениям:
![]()
где xi
– i-й предыдущий отсчет сигнала, ![]() – скользящее среднее по n предыдущим отсчетам.
– скользящее среднее по n предыдущим отсчетам.
Далее назначается так называемая граница цензурирования в виде:
|x-![]() |=tp,n-1Sx
|=tp,n-1Sx
где x – текущий сигнал, tp,n-1 - коэффициент Стьюдента, зависящий от доверительной вероятности P и числа степеней свободы n-1.
После чего все |x-![]() |>tp,n-1Sx
признаются промахами (выбросами) и удаляются из дальнейших расчетов.
|>tp,n-1Sx
признаются промахами (выбросами) и удаляются из дальнейших расчетов.
В случае отличия закона распределения случайной помехи от нормального в сторону остроконечности, необходимо увеличить вероятность P.
Для получения количественных характеристик произведем сравнение трех рассмотренных методов фильтрации, при различных параметрах. Медианный фильтр и фильтр скользящего среднего рассмотрим с шириной окна n=3 и n=5, а метод промахов рассмотрим с различными n и P, чтобы показать их влияние на результат фильтрации. При выборе этих параметров нужно руководствоваться тем, чтобы при выбранной вероятности P и количестве отсчетов n как можно больше полезного сигнала попадало в полученный интервал и при этом туда не должна попадать импульсная помеха.
В начале произведем сравнения влияния на статистические характеристики сигнала без импульсной помехи, в качестве входного воздействия зададимся сигналом с нормальным распределением, математическим ожиданием равным нулю и СКО равным единице. Полученные результаты сведем в таблицу 1. В таблице представлены: математическое ожидание (M), дисперсия (D), СКО (), асимметрия (A) и эксцесс (E) выходного сигнала.
Таблица 1.
|
Метод фильтрации |
M |
D |
|
A |
E |
|
1. Входной сигнал |
0 |
1 |
1 |
0 |
0 |
|
2. Медианный фильтр (n=3) |
-0,0002 |
0,4491 |
0,6701 |
0 |
0,03 |
|
3. Медианный фильтр (n=5) |
-0,0002 |
0,2879 |
0,5366 |
0 |
0,02 |
|
4. Фильтр скол. среднего (n=3) |
-0,0029 |
0,3333 |
0,5773 |
0 |
-0,01 |
|
5. Фильтр скол. среднего (n=5) |
-0,0034 |
0,2003 |
0,4476 |
0 |
-0,01 |
|
6. Метод промахов (n=8, P=0,99) |
-0,0008 |
0,8429 |
0,9181 |
0 |
-0,11 |
|
7. Метод промахов (n=8, P=0,999) |
0,0000 |
0,9953 |
0,9976 |
0 |
-0,04 |
|
8. Метод промахов (n=16, P=0,99) |
-0,0002 |
0,9162 |
0,9572 |
-0,01 |
-0,11 |
|
9. Метод промахов (n=16, P=0,999) |
-0,0002 |
0,9905 |
0,9952 |
0 |
-0,05 |
Как видно из полученных данных в первых четырех случаях (2-5) происходит сильное изменение статистических параметров сигнала. Так, например, при использовании медианного фильтра с шириной окна пять отсчетов оценка СКО занижена почти на 50%.
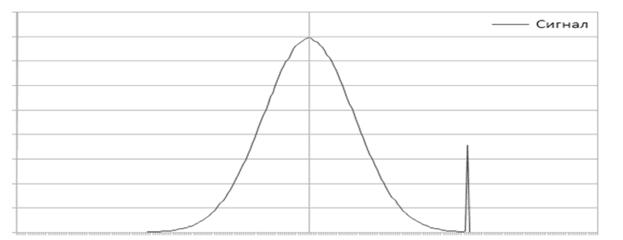
Рис. 4.
Для изучения характеристик фильтрации рассмотренных методов
воспользуемся тем же входным сигналом, но наложим на него импульсную помеху со
следующими характеристиками: амплитуда равна 3.3
исходного входного сигнала (что позволяет говорить о том, что данная импульсная
помеха не является исходным входным сигналов с вероятностью 0,999) и вероятностью появления,
равной 1%. Для моделирования такой помехи хорошо подойдет помеха с
Пуассоновским распределением ![]() и параметром =0,01 [7]. Графическое изображение плотности вероятности
распределения такого входного сигнала изображено на рис. 4. Количественные
результаты фильтрации приведены в таблице 2.
и параметром =0,01 [7]. Графическое изображение плотности вероятности
распределения такого входного сигнала изображено на рис. 4. Количественные
результаты фильтрации приведены в таблице 2.
Таблица 2.
|
Метод фильтрации |
M |
D |
|
A |
E |
|
1. Входной сигнал с имп. помехой |
0,0071 |
1,1615 |
1,0777 |
0,27 |
0,47 |
|
2. Медианный фильтр (n=3) |
0,0024 |
0,4761 |
0,6834 |
0,08 |
0,21 |
|
3. Медианный фильтр (n=5) |
0,0021 |
0,2957 |
0,5438 |
0,03 |
0,09 |
|
4. Фильтр скол. среднего (n=3) |
0,0023 |
0,3671 |
0,6058 |
0,14 |
0,17 |
|
5. Фильтр скол. среднего (n=5) |
0,0016 |
0,2203 |
0,4693 |
0,11 |
0,11 |
|
6. Метод промахов (n=8, P=0,99) |
0,0000 |
0,8576 |
0,9261 |
0,06 |
0,01 |
|
7. Метод промахов (n=8, P=0,999) |
0,0046 |
1,0871 |
1,0426 |
0,24 |
0,37 |
|
8. Метод промахов (n=16, P=0,99) |
0,0002 |
0,9283 |
0,9635 |
0,03 |
-0,11 |
|
9. Метод промахов (n=16, P=0,999) |
0,0041 |
1,0745 |
1,0366 |
0,21 |
0,32 |
После
анализа полученных результатов можно сделать ряд выводов для практического
применения рассмотренных методов фильтрации импульсных помех:
1.
Метод
скользящего среднего является неудовлетворительным по своим характеристикам,
т.к. сильно искажает входной сигнал и слабо фильтрует импульсную помеху.
2.
Медианный
фильтр отфильтровывает помеху с длительностью менее половины окна фильтра,
однако вносит сильные искажения в статистические характеристики сигнала, что
особенно сильно проявляется при увеличении ширины окна. Использование такого
фильтра при параметрическом оценивании случайного сигнала возможно лишь с последующими
корректировками характеристик.
3.
Метод
промахов показывает наилучшие результаты в фильтрации импульсных помех при решении
задач статистического анализа, т.к. слабо изменяет статистические свойства
сигнала и обладает хорошими показателями обнаружения импульсных выбросов.
Однако его применение возможно лишь при достаточно большой амплитуде импульсной
помехи (чтобы вероятность попадания сигнала в значение импульсной помехи была
менее 0,999).
Литература.
1. Давыдов А.В. Цифровая обработка сигналов: Тематические лекции. – Екатеринбург: УГГУ, ИГиГ, ГИН, Фонд электронных документов, 2005.
2. Гутников В.С. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990. – 192 с.
3.
Гонсалес
Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера, 2005.
4.
Айвазян
С.А., Мхитарян Б.Ц. Теория вероятностей и прикладная статистика. – М.:
ЮНИТИ-ДАНА, 201. – 656 с.
5.
Левин
Б.Р. Теоретические основы статистической радиотехники. М.: Радио и связь, 1989.
6.
Болтон
У. Карманный справочник инженера-метролога. – М.: Издательский дом “Додэка-XXI”,
2002.
7.
Г.
Дейвид., Порядковые статистики.– М.:Найка,– 656 с.
Поступила в редакцию 17.03.2008 г.