Принципы построения цифровых измерительных генераторов малой заданной электрической мощности с делителем на основе цифроаналогового преобразователя

 

Гусев Владимир Георгиевич,

доктор технических наук, профессор,

Косулин Иван Андреевич,

аспирант Уфимского государственного авиационного технического

университета.

 

В ряде областей науки и техники, например, при проведении биологических и медицинских исследований, а также в электрохимии, в силу существенной теплозависимости и нелинейности объектов исследования является практически невозможным получение воспроизводимых результатов при использовании традиционных методов проведения электрических измерений. Под традиционными понимаются режимы с заданным электрическим напряжением или заданным электрическим током. Невозможность их использования обусловлена тем, что параметры объекта существенно изменяются вследствие воздействия на объект электрической энергией, в результате чего результат измерения зависит как от предыдущего состояния объекта, от длительности и уровня воздействия на него, так и от ряда внешних факторов [1].

При исследовании нелинейных и теплозависимых объектов является целесообразным использование режима измерения, обеспечивающего однозначное энергетическое воздействие, в том смысле, что в объекте измерения в единицу времени будет рассеиваться заданная электрическая мощность, т.е. его термодинамическое состояние при повторных измерениях будет одинаковым в пределах значения некоторой погрешности.

На практике использование такого подхода к проведению измерений требует разработки специального класса электронных устройств, обеспечивающих неизменное значение электрической мощности, рассеиваемой в произвольном сопротивлении нагрузки, подключенной к их выходу, с погрешностью, не превышающей заданного значения, получившего название измерительных генераторов заданной электрической мощности (ИГЗМ) [2].

Один из подходов, позволяющих реализовать ИГЗМ, заключается в том, что на нагрузку осуществляется воздействие определенным электрическим параметром, например, напряжением, значение которого определяется в результате деления заданного значения мощности воздействия на значение протекающего в цепи нагрузки тока. Схема одного из вариантов такого ИГЗМ представлена на рис. 1. Идея ее работы заключается в следующем.

 

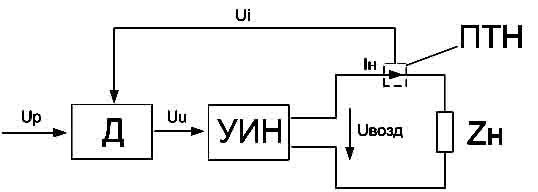
Рис. 1. Схема ИГЗМ с блоком деления на основе УИН.

 

На нагрузку Zн осуществляется непрерывное воздействие напряжением Uвозд, формируемым управляемым источником напряжения (УИН). Значение напряжения Uвозд определяется значением управляющего для УИН напряжения Uu. В свою очередь, значение напряжения Uu определяется как частное от деления напряжения Up, соответствующего значению заданной мощности Pзад, на значение напряжения Ui, характеризующего ток Iн в цепи нагрузки. Операция деления осуществляется делителем (Д), преобразование величины тока нагрузки Iн в соответствующее ему напряжение Ui – преобразователем ток-напряжение (ПТН).

Таким образом, ИГЗМ, построенные на основе схемы по рис.1, для обеспечения заданного значения рассеиваемой в нагрузке электрической мощности непрерывно воздействуют на нее напряжением Uвозд, значение которого определяется из уравнения

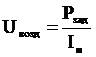                                                                                                                     (1)

или, в терминах рассматриваемой схемы,

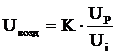                                                                                                                (2)

где  Uвозд – выходное напряжение УИН, Рзад – значение заданной мощности воздействия, Iн – ток нагрузки, Up – напряжение, определяющее Pзад, Ui – напряжение, формируемое ПТН, К – обобщенный коэффициент, учитывающий соответствие между значениями Iн и Ui, Рзад и Up, и определяемый характеристиками преобразования ПТН и УИН.

Таким образом, логика работы ИГЗМ, его быстродействие и точность во многом  определяются характеристиками используемого делителя, в зависимости от типа которого выделяют аналоговые и цифровые ИГЗМ.

В аналоговых ИГЗМ применяются микросхемы аналоговых делителей, например, AD734, AD539. Операция деления напряжения Up, характеризующего мощность воздействия, на напряжение Ui, характеризующее ток нагрузки Iн, в результате которой определяется требуемое значение напряжения воздействия Uвозд, осуществляется непрерывно. При изменении значения Up или сопротивления Zн в ИГЗМ происходит процесс установления в цепи нагрузки значения напряжения Uвозд и тока Iн, соответствующих заданной мощности рассеяния Pзад.

Аналоговые ИГЗМ обладают определенными недостатками, главный из которых - возможность потери устойчивости, связанная с тем, что в микросхемах аналоговых делителей наблюдается частичное прохождение без преобразования сигналов, поданных на отдельные входы, вследствие чего возникает положительная обратная связь. Потеря устойчивости проявляется либо в возникновении автоколебаний, либо в появлении триггерного эффекта.

 

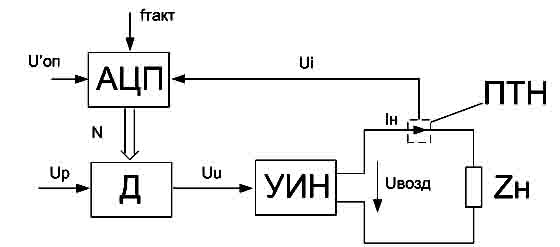
Рис. 2. Структурная схема цифрового ИГЗМ с делителем и УИН.

 

Данное явление устранено в схеме цифрового ИГЗМ, представленной на рис. 2. В отличие от схемы аналогового ИГЗМ в нее введен аналого-цифровой преобразователь (АЦП), преобразующий напряжение Ui в цифровой код N. Напряжение Uu, характеризующее напряжение воздействия на нагрузку Uвозд, формируется делителем как частное от деления напряжения Uр на цифровой код N.

Применение АЦП в рассматриваемой схеме делает иным принцип работы цифрового ИГЗМ по сравнению с аналоговым. Это обусловлено двумя обстоятельствами – периодичностью осуществления операции деления во времени, связанной с тактированием АЦП тактовым сигналом с частотой fтакт, и квантованностью представления значений Ui, обусловленной их преобразованием в цифровой код N. Рассмотрим эти моменты более подробно.

Из-за периодичности выполнения операций деления переходный процесс установления заданной мощности Рзад в цифровых ИГЗМ не является непрерывным, а представляет собой последовательность однократных операций деления осуществляемых в определенные моменты времени (итераций). 

Установление заданного значения рассеиваемой в нагрузке мощности Рзад при итерационном подходе происходит следующим образом. Если последовательно производить операции деления значения заданной мощности Pзад на значение тока нагрузки Iн, то в виде частного при каждой операции деления будем получать уточненное значение напряжения воздействия Uвозд.  После некоторого количества итераций будет получено значение напряжения Uвозд воздействие которым обеспечит рассеяние в нагрузке мощности Рзад в пределах некоторой погрешности. Общий алгоритм установления  мощности Рзад будет иметь вид

U_возд1 -> I₁ -> U_возд2=P_зад/I₁ -> U_возд2 -> I₂-> U_возд3=P_зад/I₂ -> U_возд3-> I₃ -> …

где U_воздi – рассчитанное в ходе i-й итерации значение напряжения U_возд, Ii – значение тока нагрузки используемое для его расчета в i-й итерации.

Итерационный характер процесса установления мощности обусловливает большую устойчивость цифровых ИГЗМ по сравнению с аналоговыми, поскольку действие обратной связи между ИГЗМ и нагрузкой не является непрерывным.

Включение в схему ИГЗМ АЦП приводит к возникновению инструментальной погрешности его работы связанной с преобразованием значения напряжения Ui в цифровой код N и зависящей от разрядности АЦП.

Из-за квантованности представления напряжения Ui, получаемые в результате деления напряжения Up на напряжение Ui значения напряжения Uu также будут квантованными. Поскольку напряжение воздействия на нагрузку Uвозд определяется Uu, будут квантованы и его значения. В итоге цифровой ИГЗМ будет обеспечивать воздействие на нагрузку значениями мощности Рзад, принадлежащими конечному множеству значений.

Одним из подходов, применяемых при разработке цифровых ИГЗМ, является применение делителя на основе перемножающего цифроаналогового преобразователя (ЦАП), выполненного на основе R-2R матрицы сопротивлений и КМОП-ключей, схема которого приведена на рис. 3.

 

 

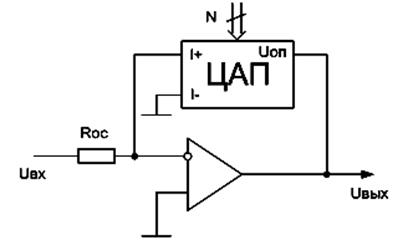
Рис. 3. Схема делителя на ЦАП.

 

Данная схема, по сути, представляет собой инвертирующий усилитель на ОУ с перемножающим ЦАП, включенным в качестве резистора обратной связи (сопротивление этого «резистора» зависит от входного кода N). Можно показать, что если в качестве резистора Rос используется резистор, расположенный на кристалле ЦАП, равный по номиналу резистору R-2R матрицы, для схемы по рис. 3 справедливо соотношение

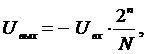                                                                                                        (3)

где n – разрядность ЦАП, N – входной цифровой код.

Таким образом, если в схеме ИГЗМ входному напряжению Uвх будет соответствовать напряжение Up, задающее значение мощности воздействия, а код N будет соответствовать напряжению Ui, характеризующему ток нагрузки Iн, то на выходе делителя получим напряжение Uвых, соответствующее напряжению Uu схемы по рис. 2.

Следует отметить, что при значении кода N «все нули», что соответствует делению на десятичный ноль, обратная связь ОУ (рис. 3) размыкается. Предотвратить возникновение данной ситуации можно каким-либо образом «запретив» данный код, либо соединив выход делителя и инвертирующий вход ОУ резистором с сопротивлением, равным Rм·2ⁿ⁺¹ (Rм – сопротивление резистора R-2R матрицы, n - разрядность ЦАП) [3]. Сложность использования второго варианта связана с необходимостью точного определения номинала резистора и согласования его ТКС с резисторами R-2R матрицы [4].

 

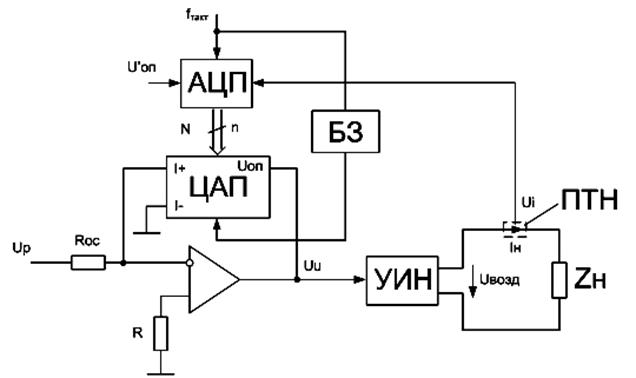
Рис. 4. Схема цифрового ИГЗМ с делителем на ЦАП.

 

Схема цифрового ИГЗМ с делителем на основе ЦАП представлена на рис. 4. Указанный на схеме блок задержки БЗ обеспечивает последовательный во времени запуск преобразования АЦП и ЦАП и приведен условно, т.к. ЦАП может начинать преобразование не по тактовому сигналу, а по сигналу готовности данных АЦП.

Работу ИГЗМ с делителем на ЦАП можно рассмотреть по временной диаграмме, приведенной на рис. 5. На ней представлено изменение уровней тока I, протекающего в нагрузке, напряжения Ui и соответствующего ему кода N, характеризующих этот ток, напряжения Uu, характеризующего напряжение воздействия на нагрузку, и рассеиваемой мощности P. Значения тока нагрузки I, напряжений Ui и Uu, при которых значение рассеиваемой мощности равно заданному значению Pзад, обозначены на диаграмме соответственно как  I’, U’i и U’u. Значения тока нагрузки I, напряжений Ui и Uu, существовавших в цепи до подключения ее к ИГЗМ, обозначены на диаграмме соответственно как  Iн, Uiн и Uuн, рассеиваемой мощности – как Рн.

 

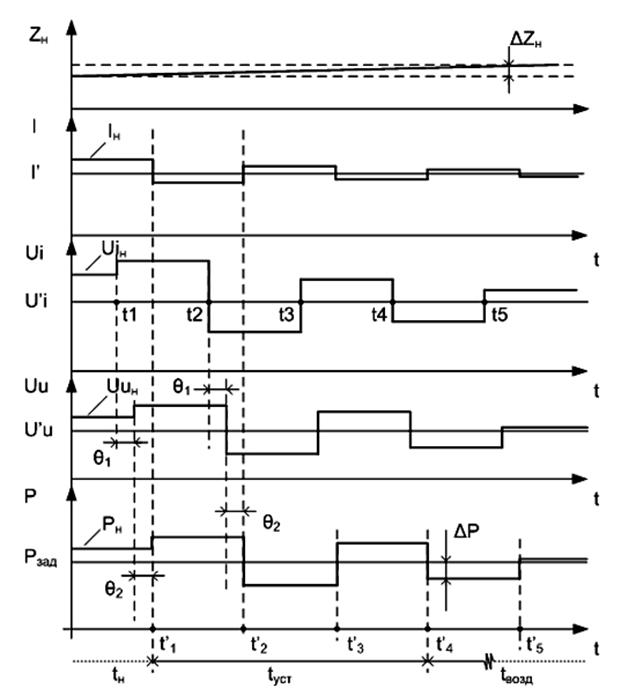
Рис. 5. Временная диаграмма работы ИГЗМ с делителем на ЦАП.

 

Тактирование работы схемы ИГЗМ соответствуют тактовым импульсам АЦП, которым на диаграмме соответствуют моменты времени t1,t2 … tn. После прихода первого тактового импульса t1 на вход АЦП код N, соответствующий полученному в момент времени t1 значению Ui, поступает в делитель на ЦАП. Из-за конечной скорости работы ЦАП, значение Uu, соответствующее частному от деления, поступает на выход делителя с некоторой задержкой θ₁. Аналогично УИН задает напряжение воздействия на нагрузку, соответствующее Uu, с некоторой задержкой θ₂, обусловленной конечной скоростью изменения выходного напряжения УИН. Этому напряжению соответствует некоторая рассеиваемая мощность P, являющаяся результатом первой операции деления. Установлению значения этой мощности на диаграмме соответствует момент времени t’1. Из-за конечных скоростей операции деления θ₁ и установления вычисленного значения выходного напряжения УИН θ₂ между измерением значения тока нагрузки I и установлением уточненного значения мощности Р существует временная задержка θ, определяемая по формуле

θ = θ₁ + θ₂.                                                                                                                            (4)

После прихода тактового импульса t2, в схеме происходят аналогичные рассмотренному процессы, приводящие к установлению в нагрузке уточненного значения мощности воздействия P в момент времени t’2 и т.д. Через некоторое число тактовых импульсов отклонение значения рассеиваемой мощности ΔP, определяемая по формуле

ΔP = P_зад – P,                                                                                                                        (5)

становится меньше некоторого значения ΔP_зад, определяющего точность ГЗМ, т.е. ΔP ≤ ΔP_зад. Этот момент времени считается окончанием режима установления мощности, обозначенного на временной диаграмме как t_уст и началом режима воздействия, обозначенным как t_возд.

Рассматриваемая схема обеспечивает непрерывный цикл операций деления и определения уточненных значений напряжения воздействия. Сходимость значений I,U,P теоретически имеет бесконечный характер, после некоторого момента времени погрешность обеспечения мощности становится меньше заданного значения и в ходе деления идет ее дальнейшее снижение. Исходя из квантованности значений тока и напряжения, с которыми работает ГЗМ, можно предположить, что  в какой-то момент времени будет достигнуто значение I при котором получаемые в результате операции деления значения Uвозд не будут являться уточненными в силу ограниченной точности преобразования напряжения Ui АЦП, обусловленной его разрядностью. При изменении параметров нагрузки или изменении напряжения Up ИГЗМ вновь переходит в режим установления мощности воздействия.

Быстродействие ИГЗМ, т.е. время его перехода в режим воздействия, зависит от значения тактовой частоты fтакт, определяющей число операций деления, выполняемых в единицу времени.

В интервалах между тактовыми импульсами на временной диаграмме значения рассеиваемой мощности Р постоянны, т.е. длительность импульсов воздействия мощностью равна периоду тактовой частоты АЦП. Отсюда следует, что период тактовых импульсов АЦП Т_ти не может быть меньше суммарного времени задержки θ, т.е. должно выполняться условие Т_ти > θ. Фактически, это является одним из критериев выбора частоты тактового сигнала АЦП fтакт.

Погрешность задания мощности и принципиальная возможность установления режима заданной мощности тесно связаны с соотношением быстродействия ИГЗМ и скоростью изменения параметров нагрузки. Под параметрами нагрузки понимаются ее активное сопротивление и состояние внутренних источников напряжения и тока. На схеме характеристика нагрузки обозначена как Z_н, ее изменение – как ΔZ_н.

Поскольку значение рассеиваемой мощности определяется уровнями  Uвозд и значением Zн, очевидно, что при недостаточном быстродействии ИГЗМ и высокой скорости изменения параметров нагрузки мы получим бесконечную процедуру определения значения Uвозд без приближения рассеиваемой мощности к заданному значению. Другими словами, из-за высокой скорости изменения Z_н в течение интервалов времени между тактовыми импульсами значение рассеиваемой мощности будет значительно меняться и ИГЗМ никогда не войдет в режим воздействия.

Таким образом, рассмотрение приведенной в данной статье схемы цифрового ИГЗМ позволяет сделать ряд выводов относительно ее практического применения. Во-первых, ИГЗМ с цифровым делителем для обеспечения заданной мощности рассеяния реализуют итерационный подход, заключающийся в осуществлении последовательных операций определения уточненного напряжения воздействия на нагрузку. Во-вторых, быстродействие ИГЗМ зависит от частоты выполнения этих операций, определяемой тактовой частотой АЦП, точность ИГЗМ – от разрядности АЦП. В-третьих, для обеспечения возможности установления заданной мощности в конкретном случае необходимо применять ИГЗМ с достаточно большим быстродействием по отношению к скорости изменения параметров нагрузки.

 

Литература

 

1. Волович Г.И. Схемотехника аналоговых и аналого-цифровых электронных устройств. М.: Додэка-XXI, 2005.

2. Гусев В.Г. Получение информации о параметрах и характеристиках организма и физические методы воздействия на него. М.: Машиностроение, 2004.

3. Демин А.Ю. Практическое применение измерительных генераторов заданной электрической мощности. // Датчики и системы, 2004, №7. – с. 38-40

4. John Wynne CMOS Multiplying DACs and Op Amps Combine to Build Programmable Gain Amplifiers, р.1, Analog Devices, AN-320A [Электронный ресурс] http://www.analog.com.

 

Поступила в редакцию 24.06.2008 г.