Решение двумерного уравнения Шредингера с полиномиальными потенциалами с дискретной симметрией методом самосогласованного базиса

Чеканов Николай Александрович,

доктор физико-математических наук, профессор,

Лукьяненко Алла Николаевна,

аспирант кафедры математического анализа.

Белгородский государственный университет.

Введение

Точные, то есть решения в явном аналитическом виде для уравнения Шредингера даже в одномерном случае найдены для небольшого класса потенциалов [2]. Поэтому разработаны и развиваются различные приближенные аналитические, так и численные методы [3]. Вычислительные трудности сильно возрастают при увеличении размерности рассматриваемой системы и усложнении вида потенциала дифференциального оператора Шредингера, для которого решается задача на собственные значения. Кроме того, точность вычислений спектра и волновых функций ухудшается, если квантовая система допускает существование динамического хаоса при ее классическом рассмотрении [4]. Так как вычисления всегда ограничены возможностями даже современных быстродействующих компьютеров, а универсального метода не существует, то приходится искать наиболее оптимальные вычислительные методы для решения конкретных задач. Перспективным современным подходом представляются комбинированные или символьно-численные методы, которые сочетают аналитические преобразования с последующим численным решением исходной задачи с использованием современных компьютерных систем как Maple, Reduce, Mathematica.

В настоящей работе рассматривается метод самосогласованного базиса [1] с использованием известной компьютерной системы Maple для решения двумерного уравнения Шредингера

Уплотнитель кабельных проходов укпт

уплотнитель кабельных проходов укпт

termofit.ru

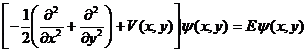                                                     (1)

со следующими тремя двумерными полиномиальными потенциалами:

,                                                  (2)

,                                                      (3)

,                                                             (4)

где  и  – спектр и волновые функции, , ,  – параметры, причем  обеспечивает дискретность энергетических спектров.

Поверхности потенциальной энергии (ППЭ) (2), (3) и (4) являются инвариантными относительно дискретных групп  (симметрия прямоугольника),  (симметрия равностороннего треугольника) и  (симметрия квадрата), соответственно. Причем параметры выбраны так, что ППЭ (2) имеет два локальных минимума и одно седло, ППЭ (3) – четыре локальных минимума и три седла, а ППЭ (4) – один минимум. Следует отметить, что во всех трех системах в классическом пределе существует классический хаос, кроме нескольких исключительных наборах параметров, что подтверждено построенными сечениями Пуанкаре.

Основные уравнения

Уравнение Шредингера (1) записывается в полярных переменных  для новой неизвестной функции  как

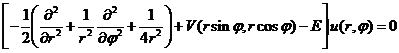,                             (5)

и его решение ищется в виде тригонометрического ряда

,                                                    (6)

где , ,   – функции от переменной . Последовательно умножая выражение (5) слева на функцию из полного набора , , ,   и интегрируя по периоду, получим, в общем бесконечную, однородную систему обыкновенных дифференциальных уравнений (ОДУ) II порядка. Эта система из-за наличия дискретной симметрии уравнения Шредингера распадается:  на четыре независимых в соответствии с четырьмя неприводимыми представлениями , , ,  группы  для ППЭ (2), на три независимых в соответствии с тремя неприводимыми представлениями , ,  группы  для ППЭ (3) и на пять независимых в соответствии с пятью неприводимыми представлениями , , , ,  группы  для ППЭ (4).

Затем каждая из полученных систем ОДУ II порядка эквивалентным образом переписываются в виде систем ОДУ I порядка и усекается до системы из  уравнений. Для полученной конечной системы ОДУ I порядка определенного типа из заданного диапазона значений энергии  численно решается задача Коши с нормальными начальными условиями, и строится общее решение, в котором содержится искомое частное решение уравнения (5), а, значит, и уравнения Шредингера (1). Учитывая граничные условия для волновой функции  в нуле и на бесконечности, получаем уже алгебраическую однородную линейную систему уравнений, нетривиальные решения которой дают нам спектр  и соответствующие волновые функции .

Результаты численных расчетов

В настоящей работе разработаны символьно-численные программы в среде Maple, с помощью которых для исходного уравнения Шредингера (1) с потенциалами (2)-(4) в соответствии с методом самосогласованного базиса проведены описанные выше аналитические преобразования, а также численные расчеты, некоторые из них представлены ниже.

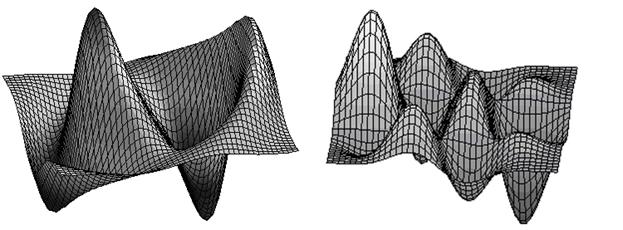
Рис.1. Рельефы волновых функций для состояния  с энергией  в  потенциале (2) с параметрами , , ,  (слева) и для состояния  с энергией  в  потенциале (4) с параметрами   (справа).

Таблица 1.

Энергетический спектр гамильтониана (1)

с  потенциалом (3) с параметрами , .

Литература

1. Виницкий С.И., Инопин Е.В., Чеканов Н.А. Препринт ОИЯИ, Р4-93-150, Дубна, 1993, 11с.

2. Миллер У., мл. Симметрия и разделение переменных. Пер. с анг. под ред. К.И. Бабенко.- М.: Мир, 1981.-342 с.

3. Турбинер А.В. Задачи о спектре в квантовой механике и процедура “нелинеаризации». УФН, Том 144, вып. 1, 1984, С. 35-78.

4. Bolotin Yu.L., Gonchar V.Yu., Tarasov V.N., Chekanov N.A. The transition regularity-chaos-regularity and statistical properties of wave function. Phys. Lett., v.A144.n.8,9, 1990, pp.459-461.

Поступила в редакцию 08.07.2008 г.