Решение уравнения Шредингера для ангармонических
осцилляторов
Чеканов
Николай Александрович,
доктор физико-математических наук,
профессор,
Флоринский
Вячеслав Владимирович,
аспирант кафедры математического
анализа.
Белгородский государственный университет.
Для многих потенциалов даже в одномерном
случае уравнения Шредингера не допускает решения в явном виде. Например,
ангармонический осциллятор с различной степенью нелинейности. Поэтому применяются
различные приближенные методы и прямые численные расчеты. Ангармоническому
осциллятору, особенно с четвертой степенью нелинейности посвящено большое число
работ (см., например [1] и ссылки в ней). Это связано с тем, что, несмотря на
кажущуюся простоту, эта модель, с одной стороны, имеет полезные приложения в
атомной и молекулярной физике, в квантовой теории поля, в теории твердого тела,
а, с другой стороны, не имеет общего решения в явном виде для собственных
значений и функций, поэтому является испытательным тестом для проверки новых
приближенных методов решения задачи на собственные значения [2]. Причина
сложности нахождения спектра и волновых функций ангармонического осциллятора в
том, что он имеет неизолированную особую точку по параметру нелинейности, если
рассматривать его в комплексной плоскости [5].
В данной работе двумя способами решается
одномерное уравнение Шредингера для ангармонического осциллятора с потенциалом
четвертой, шестой и восьмой степенями нелинейности:
(1)
(2)
где 
– пространственная
координата, 
– степень
нелинейности, 
–параметр, 
– волновая функция и 
– спектр оператора
(2).
Вначале задачу (1)-(2) приближенно решим с
помощью метода классических и квантовых нормальных форм Депри-Хори [6]. Для
этого рассмотрим классический аналог оператора гамильтониана
(2), т.е. следующую функцию Гамильтона
(3)
и представим его в виде ряда:
где числовые
коэффициенты 
находятся из выражения
(3).
Классическую
функцию Гамильтона (3) приведем к нормальной форме, т.е. найдем такую функцию 
, что
(4)
где 
– скобка Пуассона. В
выражении (4) предполагается, что старые переменные и 
зависят от новых переменных 
и 
.
Производящую
функцию 
канонического
преобразования 
и саму нормальную
форму будем искать в виде
степенных рядов
(5)
Неизвестные
величины 
и 
в выражении (5),
удовлетворяют равенству
(6)
где 
и 
– компоненты
классической гамильтоновой функции (3), а величины 
определяются
выражением
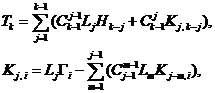(7)
где 
– биномиальные
коэффициенты, 
– оператор Ли, который
определяется через скобки Пуассона: 
.
Чтобы найти
неизвестные компоненты 
и 
, основное уравнение (6) дополним равенством (4), которое
определяет нормальную форму. Полученный в результате полином 
представим в виде суммы
двух однородных полиномов 
, удовлетворяющих условиям 
, 
. Тогда из основного уравнения (6) с учетом условия (4)
неизвестные компоненты производящей функции и нормальной формы можно определить следующим
образом 
, 
.
Для решения поставленной задачи на собственные значения (1)-(2) удобно ввести
новые комплексные канонически сопряжённые переменные
и перепишем
классическую нормальную форму в виде 
.
В настоящей работе классические нормальные формы Депри-Хори функции (3)
вычислены с помощью программы LINA [6] в среде REDUCE, которая позволяет получить
классическую нормальную форму любом заданном порядке по степени 
, ограничиваясь возможностями компьютера.
Для нахождения квантовой нормальной формы [3] воспользуемся правилом
Вейля
,
где 
, 
. Тогда собственные значения задачи
(8)
приближенно равны собственным
значениям исходной задачи (1)-(2). Ниже представлены полученные описанным выше
методом формулы для энергетических спектров гамильтониана 
(при 
соответственно):
(9)
(10)
(11)
Для решения задачи (1)-(2) составлена программа QuantaWeyl в среде
Maple, с помощью которой получены формулы (9)-(11).
Теперь решим уравнение Шредингера (1)-(2) с
помощью степенных рядов. Задача (1)–(2) эквивалентна краевой задаче
(12)
где 
– потенциальная
функция.
Будем искать фундаментальную систему решений
задачи (12) в виде рядов
(13)
где неизвестные коэффициенты 
и 
зависят от энергии и находятся подстановкой
рядов (13) в уравнение (12). Первые члены разложения линейно независимых решений
уравнения (12) 
и 
имеют вид:
:
.
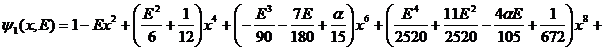
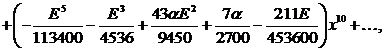
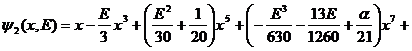
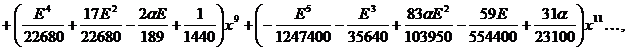
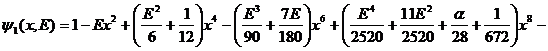
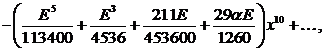
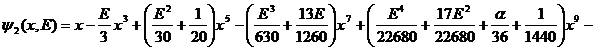
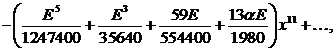
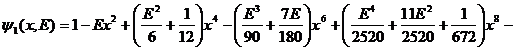
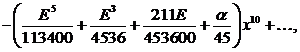
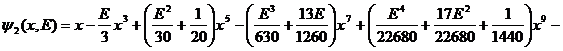
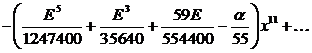Чтобы общее решение задачи (12) в виде 
удовлетворяло краевым
условиям, необходимо выбрать произвольные постоянные 
и 
так, чтобы система
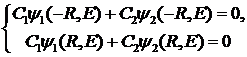(14)
имела нетривиальные решения.
На практике подбором значений параметра 
добиваемся совпадения
собственных значений в первых семи десятичных знаков, в частности, для нижних
уровней энергии в наших расчетах 
. Приравнивая к нулю определитель системы (14), получим
уравнение относительно , корни которого являются спектром задачи (1) – (2). Для каждого
вычисленного корня 
система (14) имеет
единственное решение 
и 
, поэтому волновая функция 
-го энергетического уровня имеет вид 
.
В следующих таблицах приведены сравнения значений
энергетического спектра оператора Шредингера, вычисленных в данной работе, с
результатами работы [4], в которой приведены наиболее достоверные значения спектров
ангармонических осцилляторов.
Таблица 1
Сравнение
собственных значений оператора (2),
полученных различными
методами, при , 
.
|
|
|
|
|
|
|
|
0 |
1,000748 |
1,000748 |
1,000748 |
|
|
|
1 |
3,00373 |
3,00374 |
3,00373 |
0 |
|
|
2 |
5,0097 |
5,0098 |
5,0097 |
|
|
|
3 |
7,0186 |
7,019 |
7,0186 |
|
0,017 |
|
4 |
9,0305 |
9,045 |
9,0305 |
|
0,165 |
Таблица 2
Сравнение
собственных значений оператора (2),
полученных различными
методами, при 
, 
.
|
|
|
|
|
|
|
|
0 |
1,00018 |
1,00018 |
1,00018 |
0 |
0 |
|
1 |
3,0013 |
3,0013 |
3,0013 |
0 |
0 |
|
2 |
5,0046 |
5,0047 |
5,0046 |
0 |
|
|
3 |
7,011 |
7,012 |
7,011 |
0 |
0,014 |
|
4 |
9,023 |
9,033 |
9,023 |
0 |
0,1 |
Таблица 3
Сравнение
собственных значений оператора (2),
полученных различными
методами, при 
, 
.
|
|
|
|
|
|
|
|
0 |
1,00006 |
1,00006 |
1,00006 |
0 |
0 |
|
1 |
3,00058 |
3,00059 |
3,00058 |
0 |
|
|
2 |
5,0026 |
5,0027 |
5,0026 |
0 |
|
|
3 |
7,0083 |
7,0095 |
7,0083 |
0 |
0,016 |
|
4 |
9,02 |
9,03 |
9,02 |
0 |
0,12 |
В таблицах 1-3 через 
обозначен номер
уровня; 
– значения энергии,
полученные по формулам (9)-(11); 
– значения энергии,
полученные при помощи степенных рядов; 
– значения энергии, приведенные
в работе [4]; 
и 
– относительные
отклонения рассчитанных в настоящей работе уровней энергии от их значений работы
[4]. Как видно из таблиц 1-3, имеется хорошее согласие результатов при данных
значениях параметров.
В заключение отметим, что рассмотренный метод
нормальных форм представляет некоторый вариант обычной теории возмущений и дает
неплохие результаты при достаточно малых значений параметра 
в отличие от метода
решения уравнения Шредингера с помощью степенных рядов, который пригоден при
произвольных значениях этого параметра.
Литература
1. Турбинер А.В. Задачи о спектре в квантовой
механике и процедура “нелинеаризации». УФН, Том 144, вып. 1, 1984. -c.35-78.
2. Флоринский В.В.,
Чеканов Н.А. Квантование нелинейных одномерных осцилляторов по правилу Вейля. XLIVВсероссийская конференция по проблемам
математики, информатики, физики и химии: Тезисы докладов. Секция физики. - М.:
РУДН, 2008. -с.46-47.
3. Чеканов Н.А. Квантование нормальной формы
Биркгофа-Густавсона. ЯФ, т.50.вып.8., 1989-с.344-346.
4. K. Banerjee, S.P.Bhatnagar, V. Choudhry and S.S.
Kanwal. General anharmonic oscillators. Proc. R. Soc. Lond., A360, 1978. –pp.575-586.
5. Bender C.M. and Wu
T.T. Anharmonic oscillator. Phys. Rev., v.184.No.5, 1969. – pp.1231-1260.
6. Ukolov Yu.A., Chekanov N.A., Gusev A.A., Rostovtsev
V.A., Vinitsky S.I., Uwano Y. Comp. Phis. Commun. Vol.166. No1. 2005. -pp.66 – 80.
Поступила
в редакцию 15.07.2008 г.