Решение задачи об усилении света в нестационарном ВКР при полном фазовом согласовании.
Шамров Николай
Иванович,
доктор физико-математических наук,
Логинов
Дмитрий Викторович,
старший преподаватель кафедры
Технологий программирования математического факультета Мордовского
Государственного Университета им. Н.П.Огарева.
1. Введение.
Наряду со стационарным вынужденным
комбинационным рассеянием (ВКР) [1], имеющим место для импульсов длительностью
много большей времени поперечной релаксации в КР-переходе,
в последнее время большой интерес проявляется к нестационарному,
или переходному ВКР [2]. Оно реализуется в альтернативной ситуации, когда
длительность импульса накачки меньше или сравнима со временем фазовой памяти
рассеивающих молекул. В этом случае отклик системы на внешнее излучение запаздывает,
и ВКР приобретает ряд новых, не присущих стационарному
ВКР, свойств. В условиях слабого истощения накачки [3] усиление входного
стоксового сигнала в переходном ВКР не зависит от
ширины линии КР, меньше усиления стационарного ВКР и определяется полной
энергией импульса, а не его интенсивностью [2]. Эти выводы основываются, прежде
всего, на аналитическом решении соответствующих уравнений. Однако существующее
решение получено без учета антистоксовой компонентой.
В данной работе предлагается аналитическое
решение аналогичной задачи, но с учетом антистоксовой волны. Решение получено
при условии фазового синхронизма возбуждающей, стоксовой и антистоксовой волн.
Рассматривается режим генерации, при котором излучение на смещенных частотах
зарождается в среде вследствие спонтанной эмиссии. Для решения используется широко
известный метод Римана-Вольтерра.
2. Уравнения
модели и их преобразование.
Рассмотрим ВКР лазерных импульсов мощностью ![]() 107 Вт/см2 и
длительностью
107 Вт/см2 и
длительностью ![]() 10-11
10-11![]() 10-10 с. Для такого излучения населенности уровней
молекул, участвующих в КР, не изменяются [2]. Если, кроме того, длина образца
меньше определенной [5,6], то и возбуждающее излучение
не истощается. В этом случае в пренебрежении эффектом Штарка в одномерном
приближении [7] ВКР описывается системой уравнений [5,6]
10-10 с. Для такого излучения населенности уровней
молекул, участвующих в КР, не изменяются [2]. Если, кроме того, длина образца
меньше определенной [5,6], то и возбуждающее излучение
не истощается. В этом случае в пренебрежении эффектом Штарка в одномерном
приближении [7] ВКР описывается системой уравнений [5,6]
![]() , (1)
, (1)
![]() , (2)
, (2)
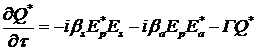 , (3)
, (3)
где ![]() – комплексные амплитуды стоксовой (
– комплексные амплитуды стоксовой (![]() ), антистоксовой (
), антистоксовой (![]() ) и накачивающей (
) и накачивающей (![]() ) волн, фазы которых считаются согласованными,
) волн, фазы которых считаются согласованными, ![]() – недиагональный элемент коллективной матрицы плотности,
определяющий поляризацию, наведенную в среде,
– недиагональный элемент коллективной матрицы плотности,
определяющий поляризацию, наведенную в среде, ![]() – скорость по поперечной релаксации,
– скорость по поперечной релаксации, ![]() – продольная координата,
– продольная координата, ![]() – запаздывающее время (
– запаздывающее время (![]() – скорость волн),
– скорость волн),
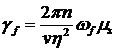 ,
, ![]()
(![]() – рамановская поляризуемость на
частоте
– рамановская поляризуемость на
частоте ![]() (
(![]() ),
), ![]() – концентрация молекул,
– концентрация молекул, ![]() – линейная часть показателя преломления). Поле накачки
– линейная часть показателя преломления). Поле накачки ![]() считается заданным и
вещественным.
считается заданным и
вещественным.
Будем полагать, что стоксово
излучение подается на образец
![]() , (4)
, (4)
![]() . (5)
. (5)
Антистоксово излучение порождается за счет
параметрического взаимодействия накачивающей и стоксовой волн, т.е.
![]() . (6)
. (6)
Введем преобразование
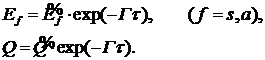 (7)
(7)
В результате уравнения (1)-(3) не содержат
релаксационного члена
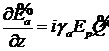 , (8)
, (8)
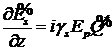 , (9)
, (9)
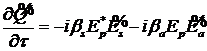 . (10)
. (10)
Перейдем в уравнениях (8)-(10) к новым
амплитудам полей ![]() . Тогда эти уравнения примут вид
. Тогда эти уравнения примут вид
![]() , (11)
, (11)
![]() , (12)
, (12)
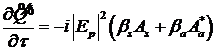 . (13)
. (13)
Легко видеть, что уравнения можно переписать
следующим образом
![]() , (14)
, (14)
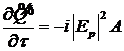 , (15)
, (15)
где ![]() – комбинация амплитуд рассеянных волн,
– комбинация амплитуд рассеянных волн, ![]() .
.
Кроме того, уравнения (1), (2) имеют интеграл
движения,
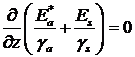 ,
,
откуда следует
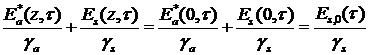 . (16)
. (16)
Введем новую переменную
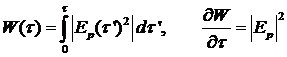 . (17)
. (17)
Величина ![]() – это энергия импульса накачки к моменту времени
– это энергия импульса накачки к моменту времени ![]() . С ее использованием уравнение (15) записывается в виде
. С ее использованием уравнение (15) записывается в виде
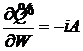 . (18)
. (18)
Уравнения (14), (18) сводятся к уравнению 2
порядка. Для этого продифференцируем уравнение (18) по переменной ![]() и учтем уравнение
(14).
и учтем уравнение
(14).
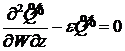 . (19)
. (19)
Аналогичное уравнение получается и для поля
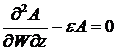 . (20)
. (20)
3. Интегрирование Римана-Вольтерра.
Пусть дано дифференциальное уравнение
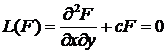 , (21)
, (21)
где ![]() – переменные
– переменные ![]() и
и ![]() .
.
Уравнение, сопряженное к уравнению (21), для
дополнительной функции ![]() в нашем случае совпадает с самим уравнением
в нашем случае совпадает с самим уравнением
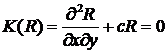 . (22)
. (22)
Рассмотрим область ![]() , в которой одновременно
, в которой одновременно ![]() и
и ![]() . Тогда
. Тогда
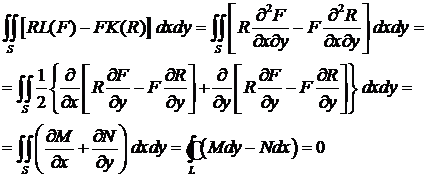 (23)
(23)
где
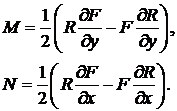 (24)
(24)
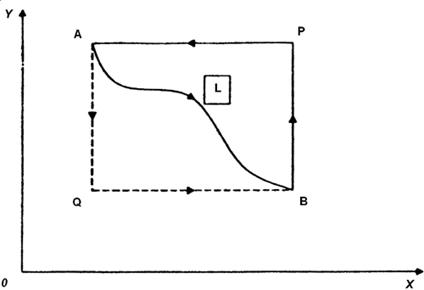
Рис.1.
Общая форма интегрирования Римана.
Для вычисления контурного интеграла выберем
контур интегрирования в виде отрезка ![]() , отрезка
, отрезка ![]() и кривой
и кривой ![]() (рис. 1). В этом
случае, принимая во внимание, что
(рис. 1). В этом
случае, принимая во внимание, что
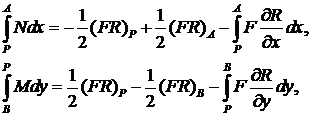
будем иметь
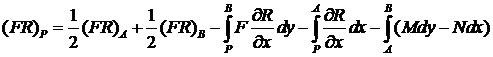 . (25)
. (25)
Выберем решение уравнения (22), отвечающее
граничным условиям
![]() ,
,
![]() вдоль
вдоль ![]() , (26)
, (26)
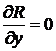 вдоль
вдоль ![]() .
.
Тогда общее решение уравнения (21) есть
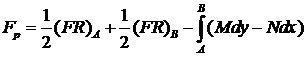 . (27)
. (27)
Кривая ![]() выбирается так, чтобы удовлетворить граничным условиям для
функции
выбирается так, чтобы удовлетворить граничным условиям для
функции ![]() . Функция
. Функция ![]() , удовлетворяющая уравнению (22) и граничным условиям (26),
называется функцией Римана для этой задачи.
, удовлетворяющая уравнению (22) и граничным условиям (26),
называется функцией Римана для этой задачи.
Вводя автомодельную переменную ![]() , уравнение (21) можно свести к обыкновенному
дифференциальному уравнению
, уравнение (21) можно свести к обыкновенному
дифференциальному уравнению
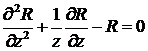 , (28)
, (28)
которое, как известно, имеет в качестве
частного решения модифицированную функцию Бесселя ![]() . Тогда функция Римана, удовлетворяющая условиям (26), есть
. Тогда функция Римана, удовлетворяющая условиям (26), есть
![]() , (29)
, (29)
где ![]() – координаты точки
– координаты точки ![]() , а
, а ![]() и
и ![]() – текущие координаты вдоль
– текущие координаты вдоль ![]() и
и ![]() (
(![]() ).
).
При граничных условиях (4)-(6) в качестве
кривой ![]() выбирают ломаную
выбирают ломаную ![]() , где
, где ![]() , а
, а ![]() . Тогда решение (27) может быть преобразовано к виду
. Тогда решение (27) может быть преобразовано к виду
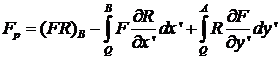 . (30)
. (30)
4. Решение уравнений. Обсуждение результатов.
Для записи общего решения уравнения (19) в
формуле (30) в качестве ![]() выберем переменную
выберем переменную ![]() , а в качестве
, а в качестве ![]() – переменную
– переменную ![]() . Кроме того, примем во внимание уравнение (18). Тогда
. Кроме того, примем во внимание уравнение (18). Тогда
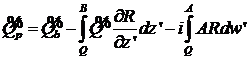 . (31)
. (31)
Аналогично для решения уравнения (20) примем ![]() за
за
![]() , а
, а ![]() за
за ![]() . В результате
. В результате
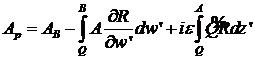 . (32)
. (32)
Выберем теперь точку ![]() за начало координат (
за начало координат (![]() ). С учетом граничных условий (4)-(6), имеем
). С учетом граничных условий (4)-(6), имеем
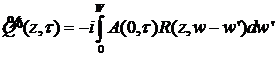 , (33)
, (33)
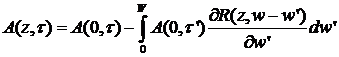 . (34)
. (34)
Примем во внимание преобразование (7) и
интеграл движения (16). В этом случае уравнения (33), (34) можно переписать
следующим образом:
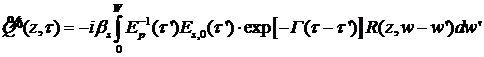 (35)
(35)
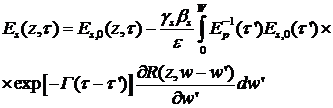 (36)
(36)
Если в формулах (35)-(36) использовать явный
вид функции Римана
![]()
и ее производной
![]()
и учесть, что ![]() , то окончательно получим
, то окончательно получим
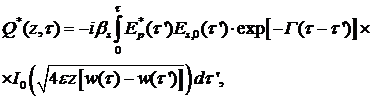 (37)
(37)
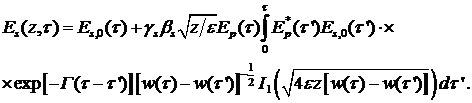 (38)
(38)
Кроме того, с учетом соотношения (16)
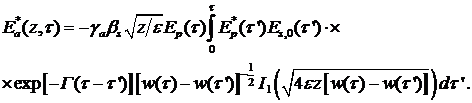 (39)
(39)
Если рассмотреть случай ![]() , т.е. положить
, т.е. положить ![]() и считать входные
импульсы накачки и Стокса подобными, т.е. принять
и считать входные
импульсы накачки и Стокса подобными, т.е. принять ![]()
![]() , то интегралы в формулах (37)-(39) можно вычислить
непосредственно.
, то интегралы в формулах (37)-(39) можно вычислить
непосредственно.
В формуле (37)необходимо перейти к новой переменной ![]() и воспользоваться
свойством
и воспользоваться
свойством ![]() . Таким образом, мы найдем
. Таким образом, мы найдем
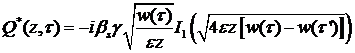 . (40)
. (40)
Для поля ![]() удобно пользоваться не
формулой (38), а выражением (36), откуда сразу получаем
удобно пользоваться не
формулой (38), а выражением (36), откуда сразу получаем
![]() . (41)
. (41)
С учетом интеграла движения (16),
![]() . (42)
. (42)
Интенсивность компонент ВКР
![]() , (43)
, (43)
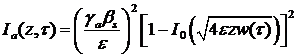 (44)
(44)
Еще раз отметим, что в формулах (40)-(44) величина ![]() .
.
При ![]() решения
для
решения
для ![]() ,
, ![]() и
и ![]() будут иметь вид,
аналогичный формулам (40)-(44), но с заменой в них функций Бесселя
будут иметь вид,
аналогичный формулам (40)-(44), но с заменой в них функций Бесселя ![]() соответственно на
соответственно на ![]() , а
, а ![]() – на
– на ![]() . Решения, подобные выражениям (40)-(44), но для импульса
накачки прямоугольной формы, получены ранее в работах других авторов.
. Решения, подобные выражениям (40)-(44), но для импульса
накачки прямоугольной формы, получены ранее в работах других авторов.
Мы видим, что интенсивность рассеянного света зависит от параметра ![]() , энергии импульса
, энергии импульса ![]() и длины системы
и длины системы ![]() . При
. При ![]() спонтанная
эмиссия, возникшая на начальной стадии, быстро затухает с течением времени.
Если
спонтанная
эмиссия, возникшая на начальной стадии, быстро затухает с течением времени.
Если ![]() , т.е.
, т.е. ![]() , то рассеянное излучение и не затухает, и не усиливается.
Эта ситуация в корне отличается от переходного ВКР в
отсутствии антистоксовой компоненты, когда усиление имеет место всегда [2].
, то рассеянное излучение и не затухает, и не усиливается.
Эта ситуация в корне отличается от переходного ВКР в
отсутствии антистоксовой компоненты, когда усиление имеет место всегда [2].
При ![]() в
случае больших усилений, т.е.
в
случае больших усилений, т.е. ![]() , пользуясь асимптотическим представлением функции
, пользуясь асимптотическим представлением функции ![]() , выражения для интенсивности (43), (44) можно записать в
виде
, выражения для интенсивности (43), (44) можно записать в
виде
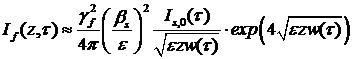 . (45)
. (45)
Усиление в основном определяется экспоненциальным членом с декрементом ![]() . Из последней формулы следует, что при полном фазовом
согласовании стоксовой, антистоксовой и возбуждающей волн антистоксов
параметрический процесс играет роль фактора, сдерживающего рост стоксова излучения. Чем больше произведение
. Из последней формулы следует, что при полном фазовом
согласовании стоксовой, антистоксовой и возбуждающей волн антистоксов
параметрический процесс играет роль фактора, сдерживающего рост стоксова излучения. Чем больше произведение ![]() , произведения
, произведения ![]() (больше
(больше ![]() ), тем эффективней протекает процесс стоксовой генерации и
тем меньше интенсивность антистоксова излучения (
), тем эффективней протекает процесс стоксовой генерации и
тем меньше интенсивность антистоксова излучения (![]() ). Если
). Если ![]() , то антистоксовым рассеянием можно пренебречь вообще [8]. Зависимость декремента усиления от энергии импульса накачки и длины
образца такая же, как и в случае переходного ВКР с отсутствующей антистоксовой
компонентой [2].
, то антистоксовым рассеянием можно пренебречь вообще [8]. Зависимость декремента усиления от энергии импульса накачки и длины
образца такая же, как и в случае переходного ВКР с отсутствующей антистоксовой
компонентой [2].
Литература.
1.
В.А.Зубов, М.М.Сущинский,
И.К.Шувалов. Стимулированное комбинационное рассеяние
света // УФН, 1964, т.83, с.197-222.
2.
С.А.Ахманов, К.Н.Драбович, А.П.Сухоруков, А.С.Чиркин. О вынужденном
комбинационном рассеянии в
поле сверхкоротких световых импульсов // ЖЭТФ, 1970, т.59, с.485-499.
3.
D.Ben-Amotz, S.M.George, C.B.Harris. Transient
stimulated Raman scattering in high laser depletion and its effects on vibrational dynamics experiments // Chem. Phys. Lett., 1983, v.97, p.533-537.
4.
P.Курант,
Д.Гильберт. Методы
математической физики. - М.: Гостехиздат, 1951, т.2,
620с.
5.
Н.И.Шамров. Нерезонансное
кооперативное комбинационное рассеяние в протяженной системе // Опт. и спектр., 1984, т.57, с.43-49.
6.
Н.И.Шамров. Эффекты
фазовой релаксации в нерезонансном кооперативном комбинационном рассеянии //
Опт. и спектр., 1984, т.57, с.623-627.
7.
Н.И.Шамров. Нестационарное
вынужденное комбинационное рассеяние: трехмерная модель и метод численного решения
// Мат. модел., 2000, т.12, №1, с.3-12.
8.
Н.И.Шамров. Квазирезонансное
приближение для кооперативного комбинационного рассеяния света // Журн. прикл. спектр., 1996, т.63,
с.91-94.
Поступила в редакцию
10.06.2008 г.