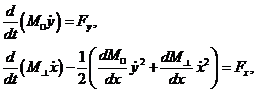Численный анализ движения сферы возле стены в идеальной жидкости

Харламов Александр Андреевич,
аспирант Московского государственного университета имени М.В.Ломоносова.

Рассматривается кинематическая задача движения сферы возле стены в идеальной несжимаемой жидкости.

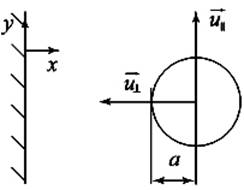
Рис. 1. Движение сферы параллельно и перпендикулярно стене.

В этой задаче нас будет интересовать траектория движения сферы и её скорость. Движение жидкости потенциально. Для простоты предположим, что на сферу не действует никаких внешних сил. Если принять систему координат как изображено на рис. 1, и без ограничения общности рассматривать плоское движение, то нас будут интересовать компоненты скорости и координаты центра сферы  как функции времени. Определяющими параметрами могут быть выбраны модуль начальной скорости , угол наклона  начальной скорости к оси, например, , начальные координаты , радиус сферы , время , плотность жидкости  и плотность сферического тела . Заметим, что в силу симметрии, координата  и время  входят в уравнения движения только как дифференциалы; следовательно, для определения характера движения важна лишь разность начальной и текущей координаты , и важен промежуток времени. Положив в начальный момент времени , мы определяем  как промежуток времени. Так же без потери общности положим . Итак, мы можем написать

.                                                                          

Безразмерных определяющих параметров слишком много для исчерпывающего анализа этой задачи, поэтому нам придется рассмотреть лишь частные случаи.

Как показано в Ламб (1951), уравнения движения одного или нескольких тел в идеальной жидкости могут быть получены применением стандартной процедуры Лагранжева формализма в обобщенных координатах. То есть определяется функция Лагранжа, равная в нашем случае кинетической энергии системы, и зависящая только от координат и скоростей тел. После этого выписываются уравнения движения .

Для сферы, движущейся в идеальной несжимаемой жидкости возле стены в плоскости перпендикулярной стене, кинетическая энергия системы равна

,                                   
и уравнения движения следующие (Ламб, 1951):

где точки над величинами означают производные по времени,  суть компоненты внешней силы на сферу, , ,  есть масса сферы,  её объем. Коэффициенты  и  суть существенные компоненты тензора присоединенных масс в используемой системе координат, являющиеся функциями безразмерного расстояния от центра сферы до стены .

Зависимости  и  были вычислены приближенно в Kharlamov et al. (2007) методом изображений и аппроксимированы с достаточной точностью простыми функциями, см. рис. 2. Здесь для расчетов используются следующие формулы:

,                                                                   

где

,                                                                                 

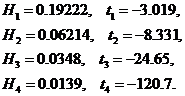
где

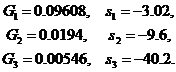
Максимальная ошибка для  составляет , для  .

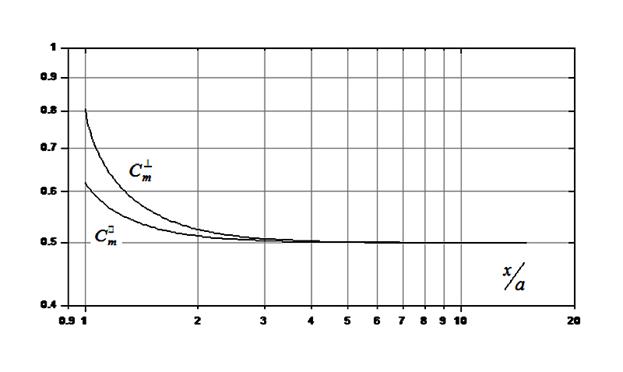
Рис. 2. Зависимости компонент тензора присоединенной массы от безразмерного расстояния до стены.

Уравнения движения были решены численно схемой Рунге-Кутта 4-го порядка. Как следует из размерного анализа, общее решение зависит от слишком большого числа параметров, поэтому могут быть рассмотрены только частные случаи решения задачи. Введем ограничения и рассмотрим наиболее любопытные движения. Будем рассматривать три случая, где отношение плотностей равно нулю, единице и 2.6 как для песка. Проанализируем всевозможные траектории движения сферы, исключив, таким образом, время и, следовательно, начальную скорость из определяющих параметров, см. . Среди переменных определяющих параметров остается только угол начального движения  и безразмерная координата начальной точки . Построим семейство траекторий, полностью описывающих возможные движения. То есть для любого угла и расстояния до стены на нашем семействе траекторий должна соответствовать одна траектория, разумеется, с определенной степенью точности, обусловленной тем, что возможно изобразить лишь конечное число траекторий.

Решение представлено на рис. 3-6. Семейство кривых делится на два подсемейства – кривые, содержащие бесконечно удаленную точку и кривые, находящиеся в полностью ограниченном пространстве. Сначала рассмотрим конечные движения. Сфера, запущенная параллельно стене на любом расстоянии до стены будет отклоняться к стене и в конечном итоге столкнется с ней. Чем дальше будет запущена сфера, тем больше будет угол между вектором скорости и стеной в момент столкновения. При приближении из бесконечности сфера натолкнется на стену под максимальным (критическим) углом, зависящим от отношения плотностей сферы и воды. Поскольку движение обратимо, то мы можем рассматривать траектории сферы начинающей свое движение от стены под различными углами. При начале движения под углом меньшим критического угла сфера опишет дугу и симметрично вернется к стене. Если начальный угол движения у стены больше критического угла, то сфера уйдет в бесконечность, слегка изменив свою траекторию недалеко у стены, рис. 6.

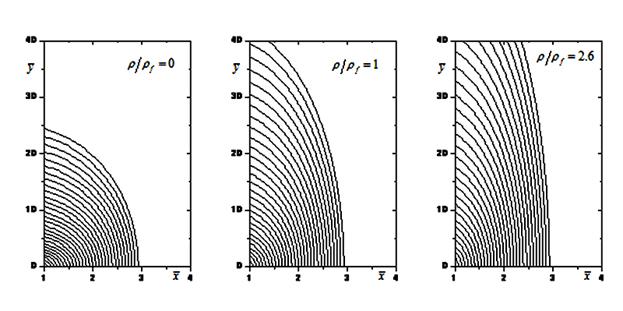
Рис. 3, 4, 5. Траектории сфер различной плотности содержащие точку с вектором скорости параллельным стене.

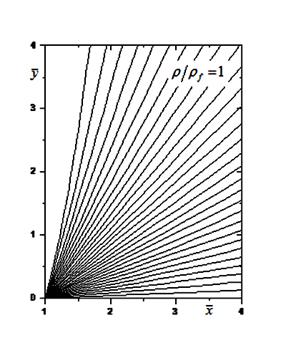
Рис. 6. Траектории сферы с плотностью равной плотности воды, начинающей движение от стены под различными углами. Траектория уходит в бесконечность.

Мы также можем определить критический угол, определяющий конечность движения, для различных расстояний до стены. На рис. 7, 8 представлены зависимости угла между вектором скорости и плоскостью стены  от расстояния до стены для различных траекторий. На рис. 7 представлено семейство кривых соответствующих ограниченному движению, с точкой начала движения параллельной стене и равномерно (в логарифмическом масштабе) удаляющейся от стены. Как видно построенные таким образом кривые имеют предельную кривую, характеризующую критический угол скорости движения в зависимости от расстояния до стены. На рис. 8 представлены оба режима движения – конечный и бесконечный. Бесконечный режим представлен семейством движений, начинающихся у стены под равномерно меняющимися углами. Поскольку для больших углов, приближающихся к , направление скорости мало меняется, то углы большие  здесь не рассматриваются ввиду того, что кривые близки к прямым линиям и не представляют интереса.

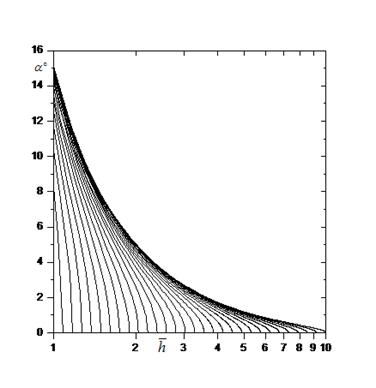
Фигура 7 Зависимость угла (в градусах) между скоростью сферы и стеной от расстояния до стены для ограниченного движения, .

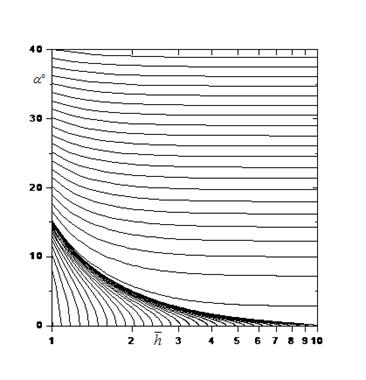
Фигура 8 Зависимость угла между скоростью сферы и стеной от расстояния до стены для ограниченного и неограниченного движения, .

Была рассмотрена кинематическая задача движения сферы возле стены в идеальной несжимаемой жидкости. Уравнения движения включают зависимости существенных компонент тензора присоединенной массы от безразмерного расстояния сферы до стены. Для компонент тензора присоединенной массы были использованы приближенные формулы, полученные методом изображений в теории потенциального течения (Kharlamov et al., 2007).

Уравнения движения сферы были решены численно при помощи популярной схемы РК-4. Траектории движения представлены для различных отношений плотностей сферы к жидкости. Проанализирован характер как ограниченного, так и неограниченного движения. Был определён критерий ограниченности движения как зависимость критического угла между вектором скорости и осью перпендикулярной стене от расстояния до стены.

Литература.

1.         Lamb. H. Hydrodynamics, 6th ed. – Cambridge: Cambridge University Press, 1951. – 738 p.

2.         Kharlamov A.A., Chara Z., Vlasak P. Hydraulic formulae for the added masses of an impermeable sphere moving near a plane wall. Journal of Engineering Mathematics, 2007, 62(2), pp.161-172.

Поступила в редакцию 06.10.2008 г.
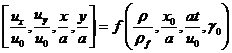