Помехоустойчивость выделения дискретного
сообщения при приёме в присутствии аддитивных помех двух
амплитудно-модулированных флуктуирующих сигналов.
Астрецов Дмитрий Вячеслалович,
кандидат технических наук,
профессор,
Валиев
Денис Азатович,
аспирант кафедры РТС,
ГОУ
ВПО «Уральский Государственный Технический Университет-УПИ».
Получено выражение для вероятности ошибки выделения бинарного сообщения, модулирующего по амплитуде два одинаковых по форме сигнала, являющихся широкополосными случайными процессами, каждый из которых принимается в присутствии взаимно независимых аддитивных широкополосных помех. Получена зависимость вероятности ошибки от параметров сигналов и отношений сигнал/помеха.
Рассматривается постановка задачи, приведённая в [1]: на входы двух пространственно разнесённых приёмных устройств поступают два амплитудно-модулированных широкополосных шумовых сигнала, отличающихся коэффициентами модуляции одного и того же сообщения, уровнями мощности, задержками во времени и фазовыми сдвигами. Оба сигнала наблюдаются в присутствии независимых аддитивных широкополосных помех, полагаемых белыми шумами с известными интенсивностями.
Функциональная схема приёма и обработки сигналов представлена на рисунке 1. Сигналы, поступающие на входы приёмных устройств через антенны А1 и А2, усиливаются, преобразуются и детектируются обычным образом, затем через устройство компенсации огибающих и усилитель низкой частоты – на решающее устройство, формирующее выходной дискретный сигнал, соответствующий принимаемому сообщению с точностью до ошибки, вызванный присутствием аддитивных помех. На приведённой схеме для упрощения не показано устройство компенсации запаздывания одного из принимаемых сигналов, а также не показан канал синхронизации.
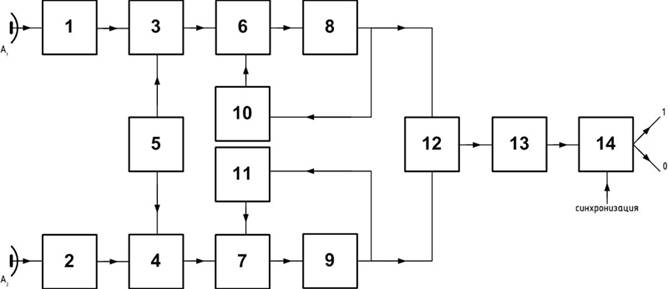
Рис. 1.
Функциональная
схема выделения дискретного сообщения при приёме двух шумоподобных
АМ сигналов: 1,2 – усилители радиочастоты; 3,4 – смесители; 5 – гетеродин; 6,7
– усилители промежуточной частоты с полосовыми фильтрами, низкочастотные
эквиваленты которых согласованы с огибающими сигналов; 8,9 – амплитудные детекторы;
10,11 – системы АРУ; 12 – устройства вычитания (компенсации); 13 – усилитель
сигналов низкой частоты; 14 – решающее устройство.
Особенностью, рассматриваемого способа обработки является использование инерционных АРУ в приемных трактах, обеспечивающих одинаковый уровень несущих шумовых колебаний на входах амплитудных детекторов, что необходимо для последующей компенсации квадратов их огибающих в блоке 12. От тщательности технического выполнения подсистемы АРУ, детектирования и компенсации существенно зависит качество выделения сообщения. В дальнейшем предполагается, что эти устройства обеспечивают идеальную компенсацию квадратов огибающих шумовых несущих в устройстве вычитания.
В дальнейшем при расчете вероятности ошибки предполагается выполнение следующих допущений:
1. Коэффициенты амплитудной модуляции малы, их разность М1-М2>0.
2. Амплитудные детекторы можно считать квадратичными.
3. Отношение мощностей сигналов к мощностям помех в каналах одинаковы и немного превышают единицу, и так как при выполнении первого допущения необходимо выделить сообщение с не слишком большой вероятностью ошибки.
4. Полосы пропускания согласованных фильтров значительно меньше ширины спектра сигнала и ширины спектра помех, а также полос предшествующих каскадов; УНЧ имеют полосы, значения которых превышают значение половины полосы каждого из согласованных фильтров.
Смеси сигналов и помех y1(t) и y2(x) на выходах линейных трактов приемных устройств в моменты времени вблизи максимальных значений огибающих можно записать в виде:
, (1)
, (2)
где K0 – коэффициент передачи линейного тракта каждого из приемных устройств,
Е(t) – огибающая несущего шумового колебания, пересчитанная на вход приемного устройства,
j(t) – флуктуирующий фазовый сдвиг несущего шумового колебания,
j0 – разность фазовых сдвигов сигналов на выходах линейных трактов каждого из приемных устройств,
l(t) – нормированное бинарное сообщение (l1=1, l0= –1),
w0 – промежуточная частота,
Е1(t), E2(t) – огибающие шумовых помех на выходах линейных трактов,
j1(t), j2(t) – флуктуации фаз помех в приемных трактах.
В связи с
тем, что несущее шумовое колебание и помехи на выходе линейных трактов являются
узкополосными случайными процессами, их огибающие имеют распределения Релея, а
фазовые сдвиги – распределения равномерной плотности [2].
Полагая, что процессы на выходах квадратичных детекторов пропорциональны квадратам огибающих процессов на их входах, можно записать:
, (3)
, (4)
где КД – коэффициент передачи детектора в каждом канале,
UД1(t), UД2(t) – процессы на выходах амплитудных детекторов в моменты времени вблизи максимальных значений сообщения.
Процесс на выходе вычитающего устройства 12 с учетом малости коэффициентов модуляции может быть записан в виде:
(5)
где учтено,
что 
, а также, что вклад векторных слагаемых в равенствах
[1+M1l(t)] и [1+M2l(t)] в энергетические характеристики помех,
учитываемых последними двумя слагаемыми в выражении (5), незначителен.
Процесс UD(t) в дальнейшем проходит через безынерционный усилитель и поступает на решающее устройство. Симметричность схемы, приведенной на рисунке 1, характер первого полезного слагае6мого равенства (5) показывает, что порог решения в этом случае должен быть равен нулю. При равных априорных вероятностях посылок «нуля» и «единицы» бинарного сообщения l(t) при этом вероятности ошибок первого и второго рода равны полной вероятности ошибки Рош. Поэтому для нахождения этой вероятности достаточно, например, найти вероятность ошибки первого рода, т.е. вероятность решения l*=1 при переходе «нуля» (l= –1):
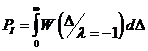, (6)
где 
– условная плотность
вероятности величины D при l= –1,
D(t)М – выражение в фигурных скобках равенства (5) в момент окончания символа дискретного сообщения, соответствующий подаче сигнала на вход решающего устройства системы синхронизации.
Для оценки закона распределения случайной величины D рассмотрим распределения слагаемых выражения в фигурных скобках равенства (5). Первое слагаемое имеет экспоненциальное распределение, так как содержит квадрат релеевской случайной величины [2].
Математическое ожидание первого слагаемого равно:
а1=<–2E2(t)(M1–M2)>= –4s4(M1–M2), (7)
где s2 – дисперсия
(мощность) несущего шумового колебания 
.
Тогда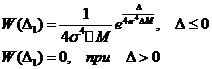 
(8)
Закон распределения разности квадратов огибающих помех в первом и втором каналах называется распределением Лапласа [2]:
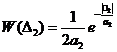, (9)
где 
, (10)
– дисперсия (мощность)
помехи 
или 
.
Такое распределение имеет разность третьего и четвертого слагаемых D3 выражения (5) в фигурных скобках с дисперсией:
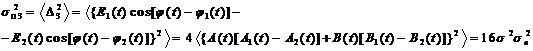(11)
Сравнивая
дисперсии величин D3
(равенство (11)) и D2 
, можно убедиться, что при 
>>, т.е. при сильных сигналах дисперсия процесса D3
значительно выше дисперсии D2 , поэтому при малых значениях разности DМ,
можно пренебречь величиной D2 по сравнению с D3. Тогда условный закон распределения
величины D
при фиксированном значении Е2 можно
записать:
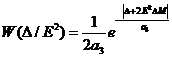, (12)
где 
.
Условная вероятность ошибки первого рода (при фиксированной Е2) при этом может быть найдена из выражения:
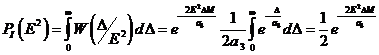, (13)
Полную (безусловную) вероятность ошибки Pош можно получить, усреднив полученное выражение по Е, учитывая, что огибающая имеет распределение Релея
Таким образом,
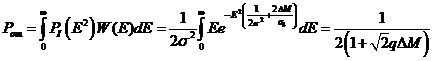, (14)
где 
– отношение
эффективных значений сигнала и помехи на выходе согласованного фильтра.
При допустимых значениях вероятности ошибки, незначительно отличающихся от 0,5, можно получить приближенную формулу:
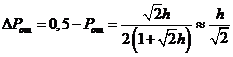, (15)
справедливую при 
. В полученной формуле 
– отклонение
вероятности ошибки от 0,5. В частности, при 
можно получить 
, что может означать при DM=10-3q=70.
Литература.
1. «Помехоустойчивость выделения сообщения при обработке двух амплитудно-модулированных широкополосных флуктуирующих сигналов». III Евро-Азиатский Форум: СвязьПромЭкспо 2006.
2.
Тихонов В.И.
Статистическая радиотехника. М.: Сов. радио, 1966
Поступила в редакцию 13.03.2008 г.