Моделирование и анализ качества переходных процессов в нечетких системах управления электроприводом

Кабылбекова Виктория Васильевна,

старший преподаватель кафедры «Транспорта и организации перевозок»,

Кулахметов Рустам Фаридович,

аспирант кафедры «Электрооборудование и автоматика судов».

Астраханский государственный технический университет.

Перспективным путем повышения качества функционирования автоматизированных электромеханических систем является использование новых современных принципов автоматического управления – адаптивного управления.

Наибольшее распространение среди интеллектуальных технологий формирования адаптивных алгоритмов регулирования и управления в области электропривода (ЭП) получила технология нечеткого управления (Fuzzy-control) [1, 2].

В работе проведен сравнительный анализ основных показателей качества переходного процесса для классической и нечеткой систем управления с целью выявления преимуществ и недостатков последней. Построены две модели систем управления: классическая двухконтурная система стабилизации скорости двигатель постоянного тока – управляемый выпрямитель (ДПТ-УВ) с ПИ-регулятором и система стабилизации ДПТ-УВ на основе нечеткого регулятора скорости. Моделирование систем стабилизации и дальнейший анализ переходных процессов осуществлялся с помощью среды моделирования Matlab Simulink.

В качестве данных для расчета применялись технические характеристики лабораторной установки, имеющейся в распоряжении кафедры «Электрооборудование и автоматика судов» Астраханского государственного технического университета. После проведения необходимых математических расчетов и выбора наиболее оптимальных передаточных функций, для каждого элемента была разработана полная функциональная схема классической двухконтурной системы стабилизации скорости ДПТ-УВ (рис.1.):

Тушенка оптом москва

Крупнокусковая тушенка оптом от завода! Высший сорт, выгодные цены, акции!

mkzargo.ru

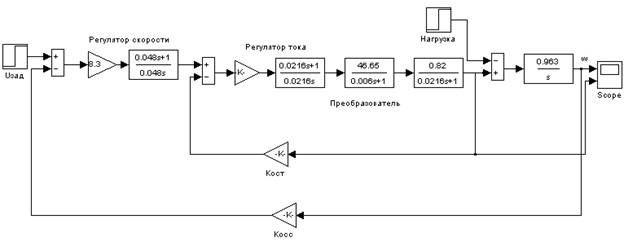
Рис. 1. Полная функциональная схема двухконтурной системы стабилизации в среде моделирования Matlab Simulink.

Для получения графиков переходных процессов на основе модели классической системы стабилизации скорости был проведен следующий опыт. Имеющиеся в составе построенной модели стандартные блоки системы Matlab - генераторы ступенчатого сигнала Step, которые в данном случае выполняют роль задающего сигнала и нагрузки, позволяют изменять свои величины в заданный момент времени. Благодаря этому, исследуемая модель будет запущена в работу со следующими условиями:

1. Система запускается с сигналом задания  о.е. и под нагрузкой  о.е.

2. В момент времени t = 7,5 с сигнал задания уменьшается вдвое.

3. В момент времени t = 15 с момент нагрузки возрастает.

При правильной настройке всех параметров системы, ее реакция по скорости на отмеченные выше скачки сигнала задания и нагрузки будет выглядеть следующим образом (рис. 2):

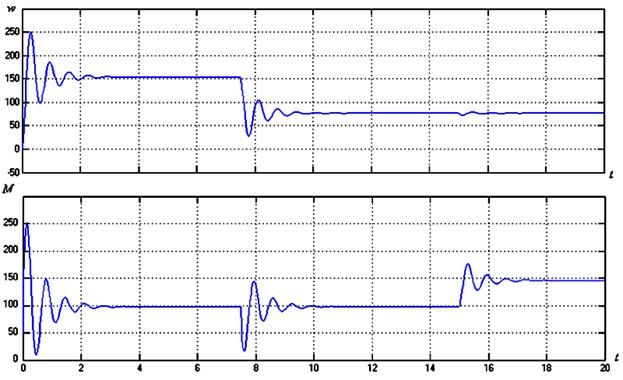
Рис.2. График переходных процессов классической системы стабилизации скорости.

Далее была построена модель системы стабилизации скорости ДПТ-УВ на основе нечеткого регулятора. Основные принципы моделирования нечеткого регулятора скорости, при помощи пакета расширения Fuzzy Logic Toolbox, для системы ДПТ-УВ описаны в статье [3].

Модель системы стабилизации скорости ДПТ-УВ с нечетким регулятором, построенная с помощью среды моделирования Matlab Simulink, представлена на рисунке:

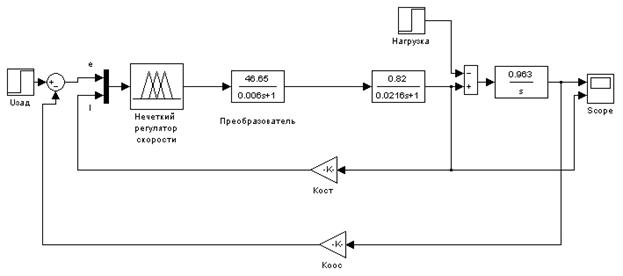
Рис. 3. Модель системы стабилизации скорости ДПТ с нечетким регулятором.

Переходные процессы, полученные с помощью данной модели, приведены на рисунке (рис. 4.):

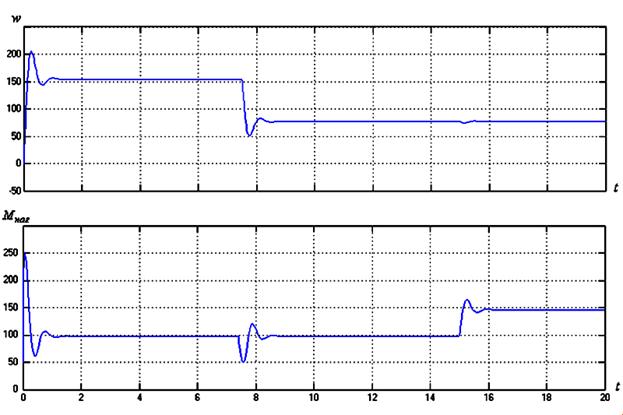
Рис. 4. Графики переходных процессов для модели системы стабилизации с нечетким регулятором скорости.

Далее проводился сравнительный анализ основных показателей качества переходных процессов по полученным графикам для построенных моделей.

Оценка качества переходных процессов проведена по следующим основным показателям: время регулирования (); перерегулирование (); частота колебаний; число колебаний (n), время достижения первого максимума (); время нарастания переходного процесса (); декремент затухания ()

Переходные процессы по скорости были рассмотрены для 3-х режимов:

1) переходной процесс при пуске под нагрузкой (t = 0c);

2) переходной процесс в момент времени t = 7.5с, когда сигнал задания уменьшается вдвое;

3) переходной процесс в момент времени t = 15с, когда нагрузка возрастает.

Цифровой анализ качества переходных процессов для исследуемых моделей, приведен в таблице 1:

Таблица 1.

Сравнительный анализ графиков переходных процессов исследуемых моделей.

По данным, приведенным в таблице, можно сделать следующие выводы:

1. Для первого режима, при пуске под нагрузкой – модель системы стабилизации скорости с нечетким регулятором обеспечивает время переходного процесса по скорости меньше, чем классическая модель (62%). Так же переходной процесс по скорости для модели с нечетким регулятором отличается меньшими значениями величины перерегулирования (35%), частоты (16.2%), числа колебаний (60%) и большей величиной декремента затухания (83.3%).

2. Для второго режима, при скачке сигнала задания – модель системы с нечетким регулятором обеспечивает на 30-35% меньшие провалы по скорости, чем модель классической системы. При этом уменьшается временем регулирования (практически в два раза) и число колебаний за время регулирования (50%).

3. Для третьего режима, при скачкообразном изменении нагрузки – модель системы стабилизации с нечетким регулятором обеспечивает меньшие провалы по скорости (45-50%), чем классическая модель, а также характеризуется меньшим значением временем регулирования (33 %) и числа колебаний (40%).

На основании полученных в ходе исследования результатов, можно сделать вывод, что замена классического регулятора скорости, на регулятор идентичной структуры, но построенный по принципам нечеткой логики приводит к существенному повышению качества переходного процесса системы.

Литература

1. Макаров И.М., В.М. Лохин, С.В. Манько, М.П. Романов Искусственный интеллект и интеллектуальные системы управления/ Отделение информ. Технологий и вычислит. систем РАН. – М.: Наука, 2006. – 333с.

2. Зайцев А.И. Применение нечетких систем управления в электроприводах./А.И. Зайцев, Г.Л. Муравьев, В.Л. Сташнёв. – www.electro.nizniy.ru// papers/4/00407.html.

3. Кабылбекова В.В, Кулахметов Р.Ф, Надеев А.И. Нечеткие системы управления тиристорными электроприводами // Датчики и системы, 2009. №5. С. 37-39.

Поступила в редакцию 28.09.2009 г.