Расчет работы, совершаемой над экструдатом в рабочем зазоре дискового экструдера
Марков
Дмитрий Васильевич,
аспирант кафедры «Автоматизированный
электропривод» Ижевской государственной сельскохозяйственной академии.
Научный руководитель – профессор, заведующий
кафедрой «Автоматизированный электропривод» Ижевской государственной сельскохозяйственной
академии,
Кондратьева
Н. П.
При расчете дискового
экструдера основной задачей является определение работы, совершаемой над
экструдатом в рабочем зазоре. Предлагаемый расчет работы, совершаемой над экструдатом,
является приблизительным, но, как показала практическая наработка, вполне
приемлем для определения требуемой мощности приводного электродвигателя
дискового экструдера. Так же представленный расчет приемлем для проверки
достаточности совершаемой в рабочем зазоре работы для обеспечения требуемой
механической и термической обработки экструдата.
Для определения необходимой для
разрушения экструдата работы необходимо определить
силы, действующие на экструдат и вызывающие
предельные напряжения.
Рассмотрим механические
напряжения, которым подвержен экструдат
в дисковом экструдере. К рассмотрению примем участок рабочего зазора при
условии, что длина этого участка стремится к нулю (l→0). Малый участок с действующими на
него нагрузками представлен на рисунке 1.
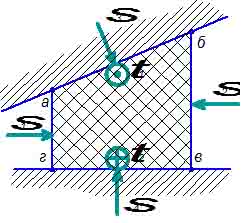
Рис. 1.
Действующие на экструдат нагрузки в рабочем зазоре
дискового экструдера.
На рассматриваемый участок
действуют как нормальные, так и касательные напряжения.
Напряжения σ3 и
σ4 – напряжения вызванные реакцией упругих элементов дисков:
действие на экструдат сил упругости дисков
уравновешиваемых силами обусловленными давлением нагнетания экструдата.
Напряжение σ2 –
напряжение вызванное действием силы давления нагнетания.
Напряжение σ1 –
напряжение вызванное разностью сил давления нагнетания экструдата
по плоскости б-в и плоскости а-г.
Под действием вышеупомянутых сил,
вызывающих напряжения, в экструдате осуществляются следующие
работы: работа над экструдатом силами реакции дисков
(поперечное сжатие); работа над экструдатом силами
трения (продольное сжатие, деформация сдвига).
Рассмотрим нормальные напряжения
малого участка экструдата, находящегося в рабочей
зоне, вызванные силами, обусловленными реакциями дисков. В соответствии с [1]
работа по деформации i-ого участка экструдата
определяется по формуле:
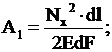 (1)
(1)
где Nx – суммарная сила
действующая на экструдат со стороны дисков
(поперечная сила);
dl – длинна i – ого участка;
Е – модуль упругости;
dF – площадь i – ого участка.
Учитывая углы
наклонов дисков экструдера относительно друг друга, выражение (1) примет следующий вид:
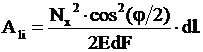 (2)
(2)
где φ
– угол между плоскостями дисков экструдера.
Выразив значение реакции дисков
через действующее давление и площадь элементарного участка, получим:
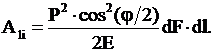 (3)
(3)
Для зоны рабочего зазора
дискового экструдера со ступенчатым изменением угла наклона дисков выражение (3)
будет иметь вид:
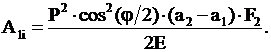 (4)
(4)
где а2
– величина входного зазора зоны;
а1
– величина выходного зазора зоны;
F2 – площадь верхнего диска.
В соответствии с [1] работа по
сжатию участка экструдата с непрерывным изменением
размеров поперечного сечения определяется по формуле:
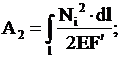 (5)
(5)
где Ni – суммарная сила, определяющая возникшие
напряжения i – ого участка;
F’ – площадь приемного
зазора;
dl – длина i-ого участка.
Так как
пространство между дисками имеет выходной зазор, то продольные (по направлению
движения экструдата) напряжения обусловлены силами
трения пар нижний диск - экструдат, верхний диск – экструдат и силами продольной составляющей сил реакции
дисков В соответствии с законом Паскаля суммарная сила
трения действующая на i – ом участке экструдата
определяется выражением
![]() (6)
(6)
где ![]() - сумма поверхностей нижнего и верхнего дисков i – ого участка;
- сумма поверхностей нижнего и верхнего дисков i – ого участка;
μ – коэффициент трения пары диск-экструдат.
Силы, действующие
на экструдат в продольном направлении, определяются
по формуле:
![]() (7)
(7)
Суммарная
сила, действующая на экструдат в продольном
направлении, будет определяться выражением:
![]() (8)
(8)
Подставив выражения (8) и (6) в
(5), получим выражение определения работы по продольной деформации экструдата:
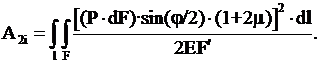 (9)
(9)
Для экструдера со ступенчатым
изменением наклона поверхности выражение (9) примет вид:
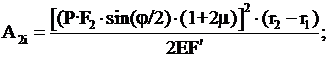 (10)
(10)
где r2 – радиус окончания рассматриваемой зоны относительно центра вращения
дисков;
r1 – радиус начала рассматриваемой зоны относительно центра вращения
дисков;
F/ – площадь приемного зазора рассматриваемой зоны.
Деформация сдвига экструдата осуществляется силами трения, обусловленными
силами реакции дисков.
В соответствии
с [1] работа по деформации сдвига элементарного участка определяется выражением:
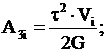 (11)
(11)
где τ
– сдвиговое напряжение;
Vi – объем элементарного i – ого участка экструдата
в рабочем зазоре;
G – модуль упругости
второго рода.
Сдвиговые напряжения определяются
по формуле [2]
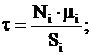 (12)
(12)
где Ni – сила реакции i – ого участка;
μi – коэффициент трения i – ого участка;
Si – площадь диска i – ого участка.
Подставив выражение (12) в (11)
получим:
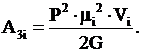 (13)
(13)
Полная работа над экструдатом определяется как сумма работ продольной, поперечной
деформации, деформации сдвига на всех участках рабочего зазора экструдера. Сумма
вышеопределенных работ расходуется на механическую обработку и нагрев экструдата. Используя общеизвестную формулу Мельникова [2]
для определения работы по измельчению материала, возможно определение работы,
совершаемой дисковым экструдером по нагреву обрабатываемого экструдата,
и определения температуры, которой можно достичь, применяя рассматриваемый
профиль рабочего зазора.
Литература
1. Борщев В. Я. Оборудование для
измельчения материалов: дробилки и мельницы: учебное пособие, Тамбов:
издательство Тамбовского Государственного Технического Университета, 2004. 75 с.
2. Клушанцев Б.В., Косарев А.И., Муйземнек
Ю.А. Дробилки. Конструкции, расчет, особенности эксплуатации. М.:
Машиностроение, 1990. 320 с.
Поступила
в редакцию 12.10.2009 г.