Разработка нелинейной математической модели процесса сжигания твёрдого топлива

 

Косенко Максим Вячеславович,

аспирант Московского энергетического института,

Кромов Иван Сергеевич,

соискатель Ивановского государственного энергетического университета,

инженер по наладке и испытаниям оборудования ОАО «Ивэлектроналадка».

 

В статье рассматриваются основы математического моделирования топочных процессов котельных агрегатов, рассчитанных на сжигание твёрдого топлива и газа. Приведены основные уравнения и допущения, применяемые при моделировании. Разработана математическая модель процесса сжигания твёрдого топлива, описанная системой нелинейных дифференциальных уравнений, включающей уравнения неравновесной термодинамики, которая может быть положена в основу автоматических систем регулирования тепловой нагрузки в котлах.

 

Задачей представленной работы являлась разработка динамической нелинейной математической модели процесса сжигания твёрдого топлива, отражающей реальные физико-химические процессы, протекающие при горении. В настоящее время на решение проблемы создания высокоточных математических моделей энергоблоков направлены усилия многих специалистов. Однако процессы сжигания топлива в топочных камерах котлов на протяжении длительного времени остаются слабым звеном при построении моделей энергоблоков. Поэтому поставленная в работе задача представляется своевременной и актуальной.

За основу процесса моделирования первоначально были положены известные математические описания физико-химических процессов горения твёрдого топлива в топочных камерах котлов в статическом режиме, наиболее полно представленные в работах профессора В.В.Померанцева и его учеников [1]. За основу динамических особенностей процессов горения топлива были взяты результаты работы В.В.Крашенинникова, П.Профоса и В.И.Бабия [2]. Инновационным же в рассмотренном подходе является использование метода феноменологической термодинамики, разработанного профессором Н.Н.Семёновым [3].

Обобщёно, процесс горения твёрдого топлива протекает при наличии следующих физико-химических процессов:

- движение в топочной камере подаваемых в неё компонентов горючей смеси;

- наличие турбулентной и молекулярной диффузии исходных веществ и продуктов реакции;

 - теплообмен в газовых потоках продуктов сгорания и исходной смеси;

 - конвективный и радиационный теплообмен горящих частиц с газовой средой;

 - процессы нагрева частиц, возгонки летучих, переноса и горения их в газовом объёме.

В связи со сложностью протекающих аэродинамических и физико-химических процессов, и их значительной зависимости от трёх пространственных координат, при создании математической модели был принят ряд допущений, а именно предполагается, что:

 - реагирование протекает на поверхности углеродных частиц сферической формы одинаковых размеров;

 - горение выделяющихся летучих веществ и догорание продуктов неполного сгорания происходит в объёме газовой среды;

 - конвективным переносом теплоты из системы и диффузионной теплопроводностью можно пренебречь.

При принятых допущениях метод феноменологического описания в данной работе заключается в том, что для описания топочных процессов горения твёрдого топлива были составлены законы сохранения массы, энергии и количества движения, являющиеся следствиями первого и второго законов термодинамики. При этом при протекании в топочной камере химических реакций и фазовых переходов в правые части уравнений законов сохранения массы для компонентов реагирующей смеси были включены удельные мощности изменения масс компонентов.

В результате общая система уравнений законов сохранения, описывающая топочные процессы, имеет вид:

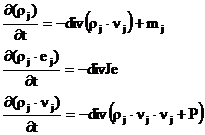
                                                                  (1)

 

где ρ_i – плотность потока переносимой массы i-го компонента в элементарном объёме;

ν_i – скорость центра масс элементарного объёма, м/c;

e – полная энергия на единицу массы i-го компонента, Дж/кг;

Je – полный удельно-массовый поток энергии, Вт/м²;

P – тензор давлений на элементарный объём, Па;

m_j – удельная мощность изменения массы j-го компонента, (кг/с)/м³.

Решение этой системы уравнений в общем виде не представляется возможным, поэтому был осуществлён переход к одномерной модели, а затем к модели с сосредоточенными параметрами.

При этом система уравнений (1) принимает следующий вид:

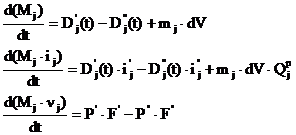                                                       (2)

где D_j’ и D_j’’– расход j-го компонента смеси на входе и на выходе моделируемой системы;

M_j – масса j-го компонента в объёме системы;

dV – объём моделируемой элементарной области;

i_j’ и i_j’’– энтальпия j-го компонента смеси на входе и на выходе моделируемой системы;

Q_j^p – теплота сгорания j-го компонента.

На примере рассмотрения горения угольной частицы комплекс (m_j·dV) для углерода частицы был выражен через скорость выгорания углерода, которая в свою очередь была найдена при допущении, что изменение констант скоростей реакций от температуры подчиняется закону Аррениуса:

                                                                                (3)

                                                                              (4)

где G_c – скорость горения углерода, кмоль/(м²·с);

M_молС = 12 - молекулярная масса углерода;

F_пов. – площадь поверхности реагирующих частиц;

k_c – константа скорости горения углерода.

Имеется обширнейший экспериментальный материал по определению кинетических констант реакции горения углерода, но следует отметить, что эти данные, полученные с применением различных экспериментальных методик на разных видах углеродного материала, отличаются большим разнообразием. В данной работе для уравнения (4) константа скорости химической реакции горения углерода (С + О₂ ↔ СО₂) была выражена через энергию активации реакции Е_с при предположении о наличии некоторой условной точки – полюса, в которой сходятся линии констант скорости реакций:

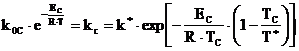                                                       (5)

где {k*; T*} = {10 м/c; 2500 К} – координаты полюса согласно [3].

Аналогичным образом, согласно (3)-(5), были выражены скорости расхода кислорода, скорости образования СО₂ и при необходимости (наличие восстановительной среды) угарного газа СО.

Для применения выражения (3) традиционно сложным и до конца не исследованным вопросом является определение площади поверхности реагирующих частиц. Данный вопрос наиболее полно рассматривался в работах Г.Т.Левита и С.Н.Миронова [4]. При разработке математической модели в рассматриваемой работе площадь пыли определялась из зерновой характеристики топлива по методике Г.Т.Левита, основанной на использовании формулы Розина – Рамлера – Беннета (РРБ). Дополнительно была введена поправка на реальную форму частиц угольной пыли, отличающуюся от сферической.

Дополнительно был выполнен расчёт концентраций оксидов азота (NO_x) в уходящих дымовых газах. Расчёт концентраций NO_x произведён на основе теории Семёнова-Зельдовича-Франк-Каменецкого при рассмотрении совокупности цепных реакций с участием атомарного кислорода и азота:

О + N₂  NO + N (6)

N + O₂  NO + O (7)

где k₁-k₄ – скорости протекания прямых и обратных реакций (6) и (7).

Кинетика реакций (6-7) определяется уравнениями [5]:

                 (8)

(9)

 

В расчете принималось допущение, что скорость изменения концентрации атомарного кислорода и азота намного меньше, чем скорость изменения концентрации оксида азота, т.е. , в результате:

                                                                                                   (10)

В свою очередь выражение (8) после ряда преобразований было сведено к виду:

                                                                (11)

где С_(NO) – равновесная концентрация оксида азота;

K² – константа равновесия реакций образования оксида азота (6) и (7);

K₀ – константа равновесия реакции диссоциации молекулы кислорода.

Константа равновесия цепных реакций образования NO:

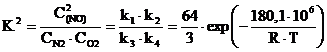                                                (12)

Согласно [ 5] для комплекса (K₀·k₁) принимается:

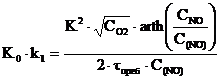                                                                          (13)

где τ_преб – время пребывания частиц в рассчитываемой зоне топочной  камеры.

Аналогичным образом был произведён учёт частичного восстановления оксидов азота в зонах с недостатком окислителя, которыми являются зона горения коксового остатка (α ≈ 0,95-1,0). Динамика процесса восстановления NO_x в указанной зоне обусловлена динамикой протекания реакции:

2NО + 2CO  N₂ + 2CO₂                                                                                (14)

Пренебрегая скоростью протекания обратной реакции, для реакции восстановления (14) справедливо:

                                                                               (15)

Путём сопоставления уравнений (11) и (15) была определена доля оксида азота, восстанавливаемого до молекулярного азота N₂ в зонах с недостатком окислителя. При этом константы скоростей реакций k₁ и k₅ были выражены через энергии активации приведённых реакций E₁ и E₅ согласно введению полюса В.В.Померанцева. Энергия активации цепной реакции образования оксидов азота (E₁ = 180 кДж/моль) была рассчитана и в дальнейшем многократно уточнена академиком Я.Б.Зельдовичем [5]. В свою очередь, энергия активации реакции восстановления оксида азота (Е₅) была рассчитана по приближённой методике Н.Н.Семёнова [3] для случая экзотермической реакции:

Е₅ = Е₀ ≈ 11,5 – 0,25Q                                                                               (16)

где Е₀ – высота потенциального активационного барьера реакции  восстановления;

Q – теплота реакции восстановления NO.

В результате общая система уравнений, описывающая топочные процессы сжигания твёрдого топлива, приведена к виду:

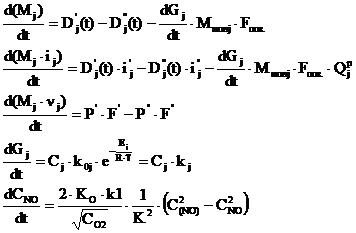                                        (17)

Полученная система отличается тем, что:

1) в правые части уравнений законов сохранения массы для компонентов реагирующей смеси были включены удельные мощности изменения масс компонентов m_j;

2) система уравнений дополнена уравнением скорости горения компонентов исходной смеси G_j, необходимым для расчета мощности изменения массы;

3) дополнительно включено уравнение для расчёта концентраций оксидов азота в продуктах сгорания рассчитываемой зоны.

 

На основе полученной системы дифференциальных уравнений, описывающих нелинейную математическую модель процесса сжигания топлива, была реализована имитационная модель топочной камеры котла в системе имитационного моделирования VisSim. Полученные результаты являются основой для синтеза автоматических систем регулирования в составе полномасштабных АСУТП энергоблоков тепловых электростанций, сжигающих твёрдое и газовое топливо.

 

Литература

 

1. Основы практической теории горения: учеб. пособие для вузов / под ред. В. В. Померанцева. – 2-е изд., перераб. и доп. – Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. – 312 с.: ил.

2. Бабий, В. И. Горение угольной пыли и расчёт пылеугольного факела / В. И. Бабий, Ю. Ф. Куваев. – М.: Энергоатомиздат, 1986. – 208 с.

3. Семёнов, Н. Н. О некоторых проблемах химической кинетики и реакционной способности / Н. Н. Семёнов. – М.: Изд-во АН СССР, 1958. – 686 с.

4. Левит, Г. Т. Пылеприготовление на тепловых электростанциях / Г. Т. Левит. – М.: Энергоатомиздат, 1991. - 384 с.

5. Зельдович, Я. Б. Физика ударных волн и высокотемпературных гидродинамических явлений / Я. Б. Зельдович, Ю. П. Райзер. – 2-е изд., перераб. и доп. - М.: Наука, 1976. – 686 с.

 

Поступила в редакцию 09.12.2009 г.