Математическое описание систем управления в канонической форме пространства состояний

Прошин Иван Александрович,

доктор технических наук, профессор,

Прошин Дмитрий Иванович,

кандидат технических наук, доцент,

Прошина Раиса Дмитриевна,

соискатель.

Пензенская государственная технологическая академия.

Идея метода канонического разложения основана на разложении передаточной функции системы на сумму простых дробей. В случае кратных корней матрица  в математической модели пространства состояний имеет Жорданову каноническую форму, т. е. является блочно-диагональной.

Пусть передаточная функция системы  имеет  полюсов с кратностями , соответственно и 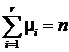. Такая передаточная функция может быть разложена на сумму простых дробей. Причем каждый полюс дает в разложении сумму простых дробей вида

.

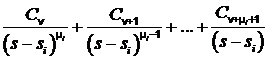Первый коэффициент  вычисляется по формуле

,

остальные из следующего выражения

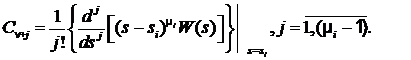                           (1)

Матрица  в модели пространства состояний с учётом (1) примет клеточно-диагональную форму

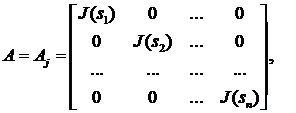                                                       (2)

где каждый элемент представляет собой матрицу – клетку Жордана порядка , отвечающую собственному значению

                                                                       (3)

Клетка Жордана (3) – матрица размера , элементы главной диагонали которой равны собственному значению , элементы  – единицы, а все остальные элементы нули.

Жорданова матрица – клеточно-диагональная матрица, в которой на главной диагонали стоят клетки Жордана, а все элементы вне этих клеток равны нулю. Составляющие вектора  равны 1 для последней строки каждой клетки Жордана  Жордановой матрицы (2), остальные – нули.

Рассмотрим особенности модели в канонической форме на примере.

Для системы с передаточной функцией

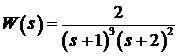,                                                                                    (4)

имеющей полюса  кратности  и  кратности , математическая модель системы в развернутой канонической форме пространства состояний принимает вид:

                                                                           (5)

Как следует из анализа модели (5), вычислению переменной  предшествует вычисление составляющей , которая зависит от _,, вычислению  предшествует вычисление переменной  являющейся, в свою очередь, функцией от , что нарушает прямую причинно-следственную связь в модели.

Суть предлагаемого метода [1] математического описания системы го порядка в канонической форме пространства состояний с прямой причинно-следственной связью состоит в том, что в матрице Жордана, для систем управления, передаточные функции

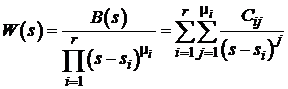                                                          (6)

которых содержат  кратных полюсов  кратности  (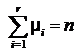), элементу, предшествующему в строках клеток Жордана диагональному, задают значение, равное 1, остальным – равное 0

,

а значения коэффициентов матрицы

вычисляют по формуле

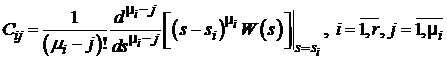.                 (7)

Модель (4) в канонической форме пространства состояний с прямой причинно-следственной связью с учётом (6), (7) можно представить так:

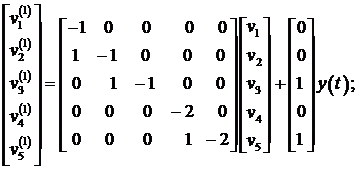
                                                                           (8)      

Из анализа полученной модели следует. Вычислению значения переменной состояния  предшествует вычисление составляющей , которая зависит от входного воздействия, вычислению составляющей  предшествует вычисление переменной  и т.д. Каждая последующая координата в модели (8) вычисляется на основе предыдущей, что соответствует принципу прямой причинно-следственной связи.

Таким образом, предложенный подход к построению математических моделей в пространстве состояний канонической формы позволяет записать модель системы управления с учётом прямой причинно-следственной связи (8) и избежать погрешностей при моделировании систем на компьютерах, обеспечить единство методологических принципов при исследовании систем управления по моделям «Вход – выход» и «Вход – состояние – выход».

Литература

1.                  Прошин И. А. Выбор фазовых координат модели системы управления в канонической форме пространства состояний // Проблемы технического управления в региональной энергетике: Сборник статей по материалам научно-технической конференции. – Пенза, 2001. С. 34 – 38.

Поступила в редакцию 20.04.2009 г.