Моделирование
и анализ компьютерных сетей
Мурадов Полад Джангир оглы,
кандидат
технических наук, доцент кафедры информатики и
телекоммуникации Азербайджанского технологического университета,
Гусейнов Закир Насиб оглы,
соискатель
кафедры информатики и экономико-математического моделирования Азербайджанского аграрного университета,
директор
интернацианальной средней школы им. Мир Джалала Пашаева, г. Гянджа,
Азербайджан.
Получены выражения для расчета вероятности отказа
для запросов первого и второго приоритетов с ограниченной очереди в
обслуживании. Получены выражения для определения среднего числа запросов
первого и второго приоритетов, среднее время ожидания в очереди для запросов
первого и второго приоритетов, вероятность вытеснения запросов второго приоритета.
Разработан алгоритм вычисления вероятности отказов в обслуживания для запросов
первого и второго приоритетов. Расчет выполнен с помощью программы Excel 2003, также составлена программа на языке Turbo Pascal.
Для анализа компьютерных
сетей воспользуемся теоремой Джексона (Jackson J.R.) [1]. Эта теорема основана
на трех допущениях:
1.
Сеть очередей состоит из N узлов, каждый из
которых представляет независимое обслуживание с экспоненциально распределенным
временем.
Водонагреватель купить в москве водонагреватель? Стоп-бактерия. Антизамерзание. Таймер нагрева aero-control.ru курсы диетсестры дистанционно перспектива.орг
2.
Запросы поступают в систему снаружи на любой из узлов с
частотой, распределенной по Пуассону.
3.
После обслуживания на узле запрос немедленно с некоторой
фиксированной вероятностью поступает на другой узел или покидает систему.
Каждый узел
может анализироваться отдельно от остальных при помощи схем M/M/1 и M/M/N, а результаты могут
комбинироваться использованием обычных статистических методов. Средние значения
времени задержки на узлах можно складывать.
Теоремы Джексона можно
использовать в сетях с коммутацией пакетов. Каждый пакет представляет собой
индивидуальный запрос. Обслуживание на каждом узле заключается в передаче
пакета, а время обслуживания пропорционально длине пакета.
Дисциплина обслуживания
с абсолютным приоритетом находит широкое применение в существующих и
разрабатываемых системах и комплексах [2-5].
В работе [3] выведены
инженерные формулы для определения характеристик обслуживания потока запросов
различных приоритетов для многоканальной системы. Рассмотрим функционирования
одноканальной одноузловой и многоузловой компьютерной сети с ограниченной
очередью и абсолютным приоритетом. Интенсивность входящей нагрузки первого и
второго приоритетов соответственно равны 
и
. Поток с номером 1 имеет абсолютный приоритет перед потоком
с номером 2.
Используя [3] для
одноканальной одноузловой компьютерной сети с ограниченной очередью и абсолютным
приоритетом получены следующие зависимости, характеризующие функционирование
сети:
Вероятность отказа для
запросов первого приоритета из-за ограничений очереди в обслуживании:
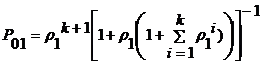(1)
где 
нагрузка первого
приоритета; 
количество мест
ожиданий:
Вероятность отказа в
обслуживании для запросов второго приоритета равна вероятности того, что в
очереди уже стоит 
запросов первого и/или
второго приоритетов:
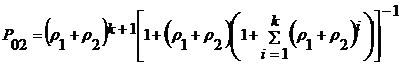(2)
где 
нагрузка второго
приоритета.
Среднее число запросов первого приоритета, стоящих
в очереди:
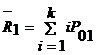(3)
Среднее число стоящих в
очереди запросов первого и второго приоритетов определяется по формуле:
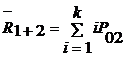(4)
Среднее число запросов
второго приоритета, стоящих в очереди, можно определить как разность между средним
числом требований первого и второго приоритетов и средним числом запросов
первого приоритета:
(5)
Среднее время ожидания
обслуживания в очереди для запросов первого приоритета:
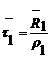(6)
Среднее время ожидания
обслуживания в очереди для запросов второго приоритета:
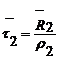(7)
Вероятность вытеснения требований второго
приоритета:
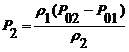(8)
Для расчета перечисленных характеристик разработан
алгоритм решение задачи.
На рис.1. приведен
алгоритм вычисления вероятности отказов в обслуживания для запросов первого
и/или второго приоритетов. Расчет по этому алгоритму выполнен с помощью
программы Excel 2003, также составлена программа на языке Turbo Pascal.
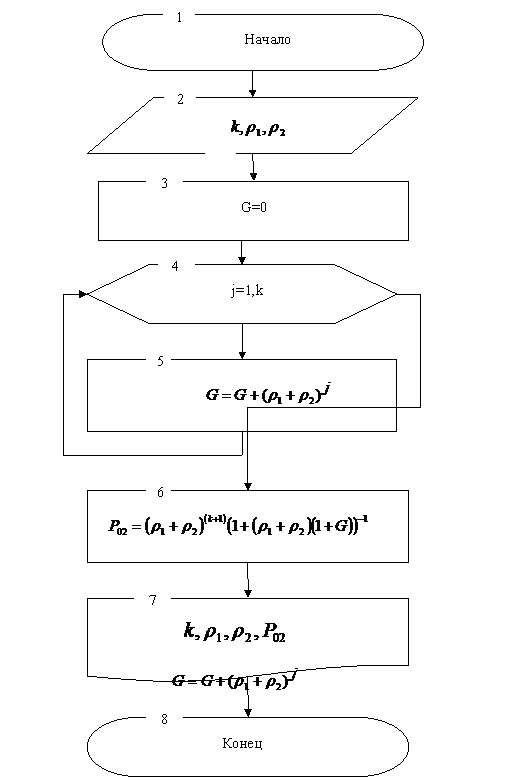
Рис. 1. Алгоритм вычисления
вероятности отказов в обслуживания для запросов первого и/или второго
приоритетов.
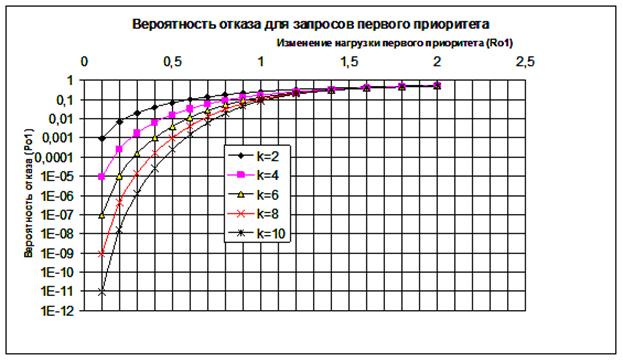
Рис. 2. Зависимость вероятности
отказов в обслуживании для запросов первого приоритета от
нагрузок первого приоритета () для определенных значений
нагрузок второго приоритета ().
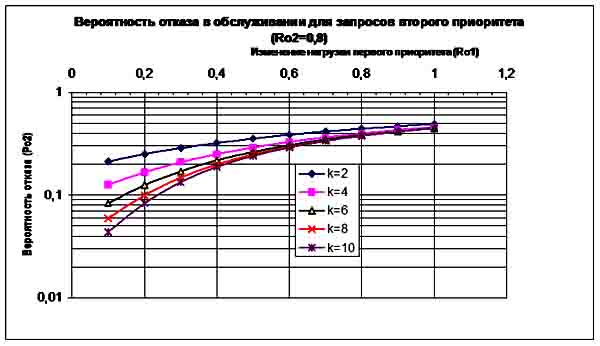
Рис. 3. Зависимость вероятности
отказов в обслуживании для запросов второго приоритета от
нагрузок первого приоритета () для определенного значения
нагрузки второго приоритета (=0,8).
На рис. 2. приведены зависимости вероятности
отказов в обслуживании для запросов первого приоритета (
) при различном количестве мест ожиданий ().
На рис. 3. приведены результаты расчетов
вероятности отказов в обслуживании для запросов второго приоритета (
) при различном количестве мест ожиданий () и нагрузок второго приоритета (
=0.8).
Из рис.2. видно, что в одноканальной одноприоритетной
сети влияние повышение количество мест ожиданий (k) на
вероятность отказов ощутимы в низких значениях нагрузки (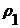) и при 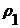>0.8 становиться незначительными. Например, при нагрузке 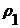=0,4 и k=2 вероятность отказа 
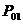=0.05, а при 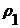=0,4 и k=6 вероятность отказа 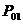=0.00001. При нагрузке 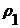=0,8, при k=2 вероятность отказа 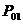=0.1, при k=6 вероятность отказа 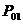=0.03.
Из рис.3.
видно, что в одноканальной сети при двухприоритетном обслуживании для
обеспечение необходимой вероятности отказов нагрузку второго приоритета () с увеличением надо уменьшить
нагрузку первого приоритета (). Например, при 
=0,8; =0.2 и k=10 вероятность отказа второго приоритета 
=0,08. В одноканальной сети, при общей нагрузки первого и
второго приоритета (
)>1, путем увеличения количества мест ожиданий (k) невозможно обеспечить
необходимой вероятности отказов, поэтому появляется необходимость создание
многоканальной сети.
Переходим на получение
математической модели многоузловой сети. Для получения математической модели
многоузловой сети можно использовать положение теории вероятности и
математической статистики. Согласно которого последовательность 
случайных событий
называется монотонно возрастающей (неубывающей) или монотонно уменьшающий
(невозрастающий), если 
для каждого 
Объединение всех событий
такой последовательности будем записывать как [6]:
или 
. (9)
Так как в многоузловых
сетях с ограниченной очередью и абсолютным приоритетом, вероятность отказа с
увеличением количество используемых узлов коммутации увеличивается, с учетом (9)
из выражений (1) и (2) для одноприоритетных и двухприоритетных обслуживаниях
можно получить математические модели для расчета вероятности отказов в
одноканальных и многоузловых компьютерных сетях. Если считать вероятности
отказов узлов одинаковыми математическая модель вероятности отказов в
одноканальных многоузловых компьютерных сетях для запросов первого приоритета
из-за ограниченной очереди в обслуживании будет иметь следующий вид:
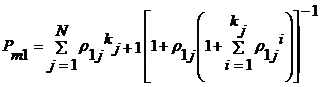(10)
где 
количество узлов сети;
нагрузка первого приоритета j-го
узла сети; 
количество мест ожиданий j-го узла сети.
Если считать вероятности
отказов узлов одинаковыми математическая модель вероятности отказов в одноканальных
многоузловых компьютерных сетях для запросов второго приоритета из-за
ограниченной очереди в обслуживании будет иметь следующий вид:
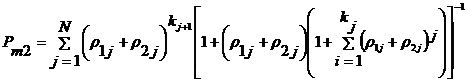(11)
При проектировании
конкретной сети связи необходимо учитывать реальной вероятности отказов
проектируемых узлов сети.
Анализ результатов, полученных
по выражению (10)
показывают, что в одноканальных многоузловых сетях для обеспечение необходимой вероятности
отказа в обслуживании для запросов первого приоритета, с увеличением количества
узлов необходимо увеличить количество мест ожиданий. Например, для обеспечения
вероятности отказа нагрузки первого приоритета 
для нагрузки первого
приоритета 
при количество узлов N=2 требуемое количество мест ожиданий k=24, при N=3 требуемое количество мест ожиданий k =26, при N=4 требуемое количество мест ожиданий k=28.
Анализ результатов, полученных
по выражению (11)
показывают, что в одноканальных многоузловых сетях при двухприоритетных
обслуживаниях, для
обеспечение необходимой вероятности отказа в обслуживании запросов второго приоритета (
) появляются необходимость создание многоканальной
многоузловой сети. Например, в одноканальной двухузловой сети (N=2) при , =0,3 и k=30 вероятности отказа в обслуживании запросов второго приоритета =0.191. При N=3, , =0,3 и k=30 вероятности отказа в обслуживании запросов второго приоритета =0.286.
Выводы
1.
В одноканальной одноприоритетной сети влияние повышение
количество мест ожиданий (k) на вероятность отказов ощутимы в низких значениях
нагрузки () и при >0.8 становиться незначительными. Например, при нагрузке =0,4 и k=2 вероятность отказа =0.05, а при =0,4 и k=6 вероятность отказа =0.00001. При нагрузке =0,8 и k=2 вероятность отказа =0.1, а при =0,8 и k=6 вероятность отказа =0.03.
2.
В одноканальных многоузловых сетях, с увеличением количества узлов, для обеспечения необходимой вероятности отказа
в обслуживании для запросов первого приоритета, необходимо увеличить количество
мест ожиданий. Например, для обеспечения вероятности отказа нагрузки первого
приоритета для нагрузки первого
приоритета при количество узлов N=2 требуемое количество мест ожиданий k=24, при N=3 требуемое количество мест ожиданий k =26, при N=4 требуемое количество мест ожиданий k=28.
3.
В одноканальных многоузловых сетях при двухприоритетных обслуживаниях, для обеспечения необходимой вероятности отказа
в обслуживании запросов второго приоритета () появляются необходимость создание многоканальной
многоузловой сети. Например, в одноканальной двухузловой сети (N=2) при , =0,3 и k=30 вероятности отказа в обслуживании запросов второго приоритета =0.191. При N=3, , =0,3 и k=30 вероятности отказа в обслуживании запросов второго приоритета =0.286.
Литература
1.
Современные компьютерные сети. 2-ое изд./ В.Столлингс. –
СПб.: Питер, 2003.- 783 с.
2.
Башарин Г.П., Бочаров П.П., Коган Я.А. Анализ очередей в вычислительных
сетях: Теория и методы расчета. М.:Наука, 1989.-336с.
3.
Булгаков Н.Н., Мирошников В.И., Шибанов В.С.
Многоканальная система с ограниченной очередью и абсолютным приоритетом.
«Вопросы радиоэлектроники», сер. ТПС, 1974, вып.5. с.21-28.
4.
Вишневский В.М. Теоретические основы проектирования
компьютерных сетей. М.: Техносфера, 2003.- 512 с.
5.
Гасанов А.Н. Анализ телекоммуникационных сетей, Баку:
«Элм», 1995, 160 с.
6.
Штермер Х. и др. Теория телетрафика. Пер. с немецкого,под
ред. Г.П.Бошарина. М. «Связь», 1971.
Поступила в редакцию 06.05.2009 г.