Построение математических моделей объектов исследования в условиях интегрированного комплекса сетевых автоматизированных лабораторий

НА ГЛАВНУЮ

Прошин Иван Александрович,

доктор технических наук, профессор,

Прошин Дмитрий Иванович,

кандидат технических наук, доцент,

Прошина Раиса Дмитриевна,

соискатель.

Пензенская государственная технологическая академия.

Интегрированный комплекс сетевых автоматизированных лабораторий (ИКСАЛ), представляя собой интегрированную автоматизированную систему управления, наделён рядом дополнительных возможностей, отличающих его от промышленных интегрированных автоматизированных систем управления [1 – 5]. Прежде всего, в ИКСАЛ включены наряду с функциями управления и организации функционирования и взаимодействия многофункциональных объектов исследования, функции по исследованию математических моделей (ММ), проведению научных исследований, как на экспериментальных установках, так и на ММ. ИКСАЛ связывает программные комплексы обработки информации и идентификации математических моделей объектов управления, модули по анализу, синтезу и проектированию систем управления.

Задача построения математических моделей многофункциональных объектов исследования и других объектов научных исследований (ОИ) в ИКСАЛ сводится, как правило, к определению структуры модели объекта и восстановлению её параметров.

Построение и экспериментальная проверка модели, т.е. математическое описание интересующих исследователя связей и отношений между реальными элементами анализируемой системы, обычно основаны на одновременном использовании информации двух видов:

1) априорной информации о природе и характере исследуемых соотношений (априорные знания);

2) исходных статистических данных, характеризующих процесс и результат функционирования анализируемой системы (апостериорные знания).

В качестве основы для классификации объектов выберем степень предварительной изученности объекта. При наличии априорной информации все ОИ могут быть разделены на следующие группы [6] (рис. 1):

· объекты, для которых известны описывающие их динамику операторные уравнения (например, дифференциальные уравнения) вплоть до приблизительных значений коэффициентов;

· объекты, для которых известны описывающие их динамику операторные уравнения, а численные значения коэффициентов неизвестны;

· объекты, для которых конкретный вид уравнения и численные значения параметров неизвестны, но имеется некоторая априорная информация (объект линеен, объект содержит нелинейность определенного вида и т.д.);

· объекты, относительно которых отсутствуют какие-либо априорные сведения (объекты типа «чёрный ящик»).

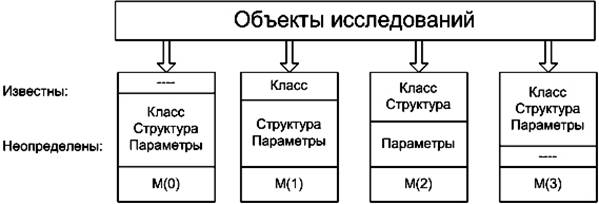
Рис. 1. Классификация объектов по степени изученности.

Провести чёткую границу между любой парой смежных групп в общем случае затруднительно.

Представим механизм идентификации модели как процесс повышения ранга модели – сокращения неопределённости модели посредством выбора из множества моделей 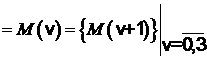требуемой за счёт привлечения дополнительной информации об объекте. Задача построения модели нетривиальна только в том случае, когда множество содержит более одного элемента, т. е. имеется исходная неопределённость. Модели третьего ранга полностью определены (табл. 1) и соответствуют ОИ первой группы (рис. 2).

Наименьшая неопределённость при решении задачи идентификации соответствует заданию множества моделями второго ранга неопределённости:

Таблица 1.

Модели различных рангов неопределённости.

Ранг ()	Модель	Класс	Структура	Параметры
0		–	–	–
1		+	–	–
2		+	+	–
3		+	+	+

При такой постановке ищется множество полностью определённых моделей систем третьего ранга, когда известны (см. табл. 1):

· класс модели объекта;

· структура операторов элементов модели,

неопределены: параметры модели ОИ.

Требуется из множества выбрать модель с известными параметрами, т.е. найти единственную модель или подкласс моделей . Таким образом, первая и наиболее простая задача – задача параметрической идентификации состоит в поиске параметров модели, удовлетворяющих заданным критериям, что соответствует повышению ранга неопределённости модели системы со второго до третьего . Такие объекты относятся ко второй группе.

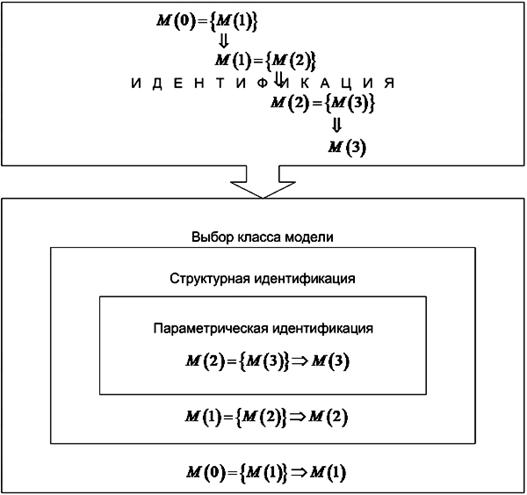
Рис. 2. Вложенная структура идентификации математической модели.

Элементы исходного множества могут различаться структурами операторов и могут быть заданы моделями первого ранга неопределённости:

т. е. множеством полностью определённых моделей систем второго ранга, когда известен (табл. 1):

· класс модели

и неопределены:

· структура операторов модели;

· параметры модели.

Требуется из множества выбрать модель с известной структурой операторов, т.е. найти единственную или подкласс моделей . В частном случае может решаться задача подбора функциональной зависимости для модели известного класса путём вариации видов функциональных преобразований.

В результате решения второй задачи – задачи структурной идентификации выбирается подмножество структур операторов (в частном случае – единственная структура), что соответствует повышению ранга неопределённости модели с первого до второго . Объекты, задаваемые множествами моделей второго ранга, образуют третью группу.

Множество может быть задано моделью нулевого ранга неопределённости (максимальная степень неопределённости):

т. е. множеством полностью определённых моделей систем первого ранга (множеством моделей различных классов), когда неопределены (табл. 1):

· класс модели;

· структура операторов модели;

· параметры модели.

Требуется из множества выбрать ММ известного класса, т.е. найти единственную или подкласс моделей . Объекты, задаваемые множествами моделей первого ранга, образуют четвёртую группу.

В результате решения третьей задачи выбирается подмножество классов (в частном случае – единственный класс), что соответствует повышению ранга неопределённости модели с нулевого до первого .

Совокупность решаемых задач построения ММ (рис. 2) образует вложенную структуру, в которой выбор класса модели в качестве внутренних включает задачи структурной и параметрической идентификации. В свою очередь выбор структуры модели охватывает решение задач параметрической идентификации.

Идентификация включает в себя следующие этапы (рис. 3) [6].

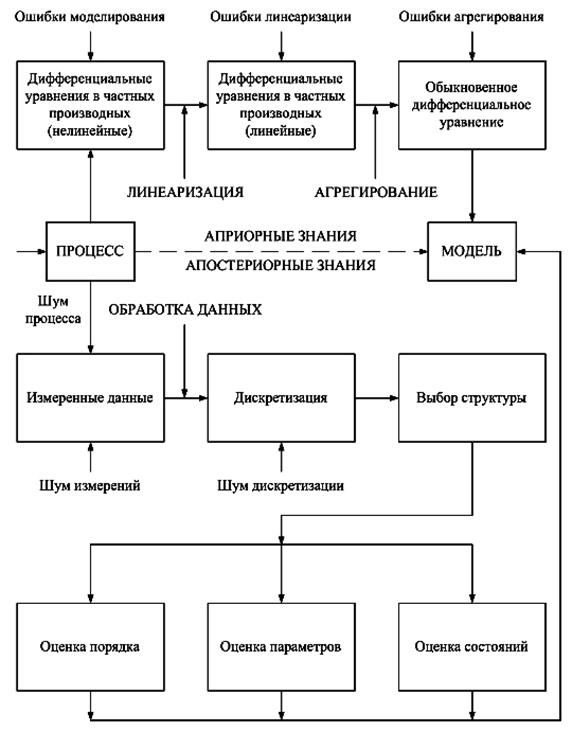
Рис. 3. Этапы построения модели.

1. Изучение объекта исследования с точки зрения действующих на него воздействий. На этом этапе исследователь должен ответить на следующие вопросы:

· какие воздействия действуют на объект;

· какие воздействия, действующие на объект, являются управляющими, возмущениями, помехами;

· какие переменные, характеризующие поведение объекта, могут быть приняты за координаты состояния, за выходные координаты;

· какова рабочая точка объекта (номинальный режим).

Результатом этого этапа должна быть структурная схема объекта с указанием действующих на него воздействий, координат состояния и выхода.

2. Изучение объекта управления с точки зрения его свойств.

Из априорных знаний об объекте (уравнений, описывающих физические процессы, протекающие в нем) и из проведенных исследований необходимо ответить на вопрос о:

· непрерывности (дискретности);

· линейности (нелинейности);

· стационарности (нестационарности);

· детерминированности (стохастичности);

· сосредоточенности (распределённости) параметров.

На основании этих данных выбирается класс моделей, используемый в дальнейшем. Таким образом, результатом второго этапа является выбранный класс моделей.

3. Выбор тестирующих сигналов и формирование записей входных – выходных сигналов. (Проведение пассивного или активного эксперимента).

При активном эксперименте на этом этапе производится выбор тестирующих сигналов и формирование записей входных – выходных сигналов, а при пассивном – формирование записей входных – выходных сигналов.

4. Определение структуры модели.

Из априорных сведений об объекте необходимо определить максимально возможный порядок модели и произвести структурную идентификацию.

Результат этапа – структура модели.

5. Оценивание коэффициентов модели.

На этом этапе выбирается метод оценивания, и определяются коэффициенты модели.

6. Проверка адекватности модели объекту.

Для ряда тестовых сигналов проверяется соответствие модели и идентифицируемого объекта.

Пункты 1 и 2 относятся к стадии изучения идентифицируемого объекта, когда требуется из множества выбрать ММ известного класса, т.е. найти единственную или подкласс моделей , 4 – к структурной идентификации, что соответствует повышению ранга неопределённости модели с первого до второго , 5 – к параметрической идентификации, когда ранг неопределённости модели повышается с второго до третьего , 6 – к проверке модели.

Классификация объектов по степени предварительной изученности и представление механизма построения модели в виде вложенной структуры позволяет определить требования к методам автоматизированного построения моделей. При автоматическом выборе структуры модели наиболее важным является быстродействие, поскольку структурная идентификация модели требует многократного повторения процедуры параметрической идентификации. В тоже время, требования к точности расчёта оценок параметров могут быть снижены до уровня, достаточного для различения моделей наиболее близких структур.

Последний этап параметрической идентификации, напротив, должен обеспечивать повышенную точность расчёта оценок ММ, так как полученные на этом этапе оценки моделей являются окончательными. При этом требования к быстродействию оценивания параметров модели могут быть ослаблены, так как параметры ММ на этом этапе достаточно вычислить только один раз.

Литература

1. Прошин И.А., Прошин Д.И., Прошина Р.Д. Концепция построения лабораторной базы в вузе / Академия профессионального образования. – Санкт- Петербург. – 2006. – № 5. – С. 20 – 24.

2. Прошин И.А., Прошин Д.И., Прошина Р.Д. Интегрированная система комплексных сетевых автоматизированных лабораторий / Академия профессионального образования. – Санкт- Петербург. – 2006. – № 2. – С. 23 – 29.

3. Прошин И.А., Прошин Д.И., Прошина Р.Д. Концепция интегрированных комплексов сетевых автоматизированных лабораторий с использованием виртуально-физической среды / Журнал научных публикаций аспирантов и докторантов. – Курск. – 2008. – № 12. – С. 33 – 37.

4. Прошин И.А., Прошин Д.И., Прошина Р.Д. Концепция интегрированных комплексов сетевых автоматизированных лабораторий с использованием виртуально-физической среды / Журнал научных публикаций аспирантов и докторантов. – Курск. – 2008. – № 12. – С. 33 – 37.

5. Прошин И.А., Прошин Д.И., Прошина Р.Д. Интегрированный комплекс сетевых автоматизированных лабораторий / Журнал научных публикаций аспирантов и докторантов. – Курск. – 2009. – № 3. – С. 127 – 130.

6. Структурно-параметрический синтез математических моделей в задачах обработки экспериментально-статистической информации / И.А. Прошин, Д.И. Прошин, Н.Н. Прошина– Пенза: ПГТА, 2007. – 178 с.

Поступила в редакцию 20.05.2009 г.