Cистематизация математических моделей систем управления в виде передаточных функций

НА ГЛАВНУЮ

Прошин Иван Александрович,

доктор технических наук, профессор,

Прошин Дмитрий Иванович,

кандидат технических наук, доцент,

Прошина Раиса Дмитриевна,

соискатель.

Пензенская государственная технологическая академия, кафедра «Автоматизация и управление».

Множество и специфика решаемых при анализе и синтезе систем автоматического управления (САУ) задач часто приводит к противоречивым требованиям к математическим моделям (ММ), применяемым при исследовании САУ, что вызывает необходимость использования различных форм записи передаточных функций (ПФ).

Математические модели САУ должны отражать физический смысл и причинно-следственную связь преобразования входных воздействий в выходные сигналы и одновременно быть удобным и действенным средством решения задач анализа и синтеза систем, эффективным средством, как при проектировании САУ, так и при реализации управляющих воздействий в них.

Как показывает анализ, для записи передаточных функций в изображениях по Лапласу в теории автоматического управления наиболее часто используются следующие три формы:

● полиномиальная форма;

● факторизованная форма;

● стандартная форма.

Для исследования сложных систем предлагается ввести понятие стандартно-факторизованной формы ПФ. Для сокращённой записи моделей сложных нелинейных систем используются передаточные функции в операторной форме. Таким образом, для исследования, анализа и синтеза САУ на основании выше изложенного предлагается систематизация передаточных функций, показанная на рис.1.

Передаточные функции, представленные в различных формах, отражают механизм преобразования входного воздействия в выходную координату для одной и той же системы и поэтому тождественно равны между собой.

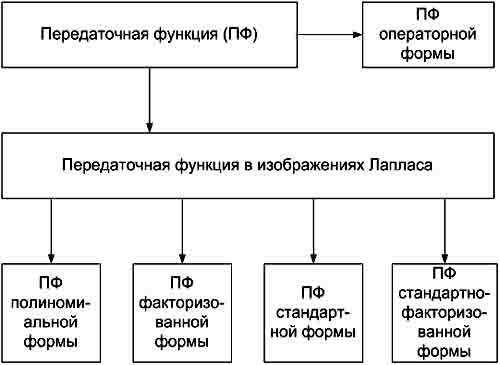
Рис. 1. Формы передаточных функций.

Передаточная функция полиномиальной формы следует непосредственно из математической модели САУ в виде дифференциального уравнения (ДУ) общего вида. Она представляет собой дробно-рациональную функцию, задаваемую в виде отношения полиномов канонической формы записи

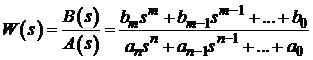. (1)

Эта форма ПФ эффективно используется при оценке устойчивости САУ, преобразовании к моделям в виде дифференциальных уравнений общего вида и «Вход – состояние – выход» нормальной формы, не требует для представления моделями в виде дифференциальных уравнений сложных вычислений, записывается уравнениями с действительными коэффициентами и при комплексных корнях характеристического уравнения.

Однако, ПФ в полиномиальной форме (1), описывая САУ в целом, не позволяет выявить структуру преобразования воздействий в системе, детализировать исследования сложных топологий систем. Коэффициенты моделей в этой форме записи не имеют ясного физического смысла, а непосредственный аналитический переход к временным характеристикам затруднён и требует дополнительных вычислений.

Передаточная функция стандартной формы – это представление передаточной функции в виде произведения статического коэффициента передачи и отношения полиномов со свободными членами, равными единице

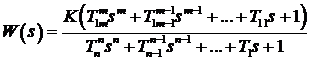. (2)

Переход к передаточной функции стандартной формы (2) позволяет получить модель, в которой параметры ПФ – коэффициенты имеют ясный физический смысл. Статический коэффициент передачи – это степень преобразования входного воздействия в выходную переменную САУ в статическом режиме, а постоянная времени характеризует быстродействие элементов или системы в целом и имеет размерность времени .

Вместе с тем в такой форме записи ПФ сохраняется низкий уровень структурированности математической модели САУ на отдельные звенья и трудности аналитического вычисления временных характеристик (нахождение обратного преобразования Лапласа).

Разложение полиномов числителя и знаменателя ПФ в соответствии с основной теоремой алгебры (теоремой Безу) на простые множители через нули и полюса

;

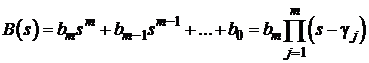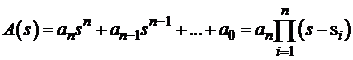
позволяет перейти к ПФ факторизованной формы

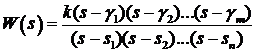. (3)

Передаточная функция факторизованной формы (3) позволяет представить целостную систему как совокупность последовательно соединённых элементарных звеньев, имеющих простейшие ПФ (рис. 2), а её разложение на простые дроби

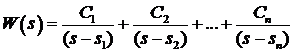(6)

приводит к представлению структуры САУ в виде параллельного соединения простейших звеньев (рис. 3).

Рис. 2. Последовательная структура ПФ факторизованной формы.

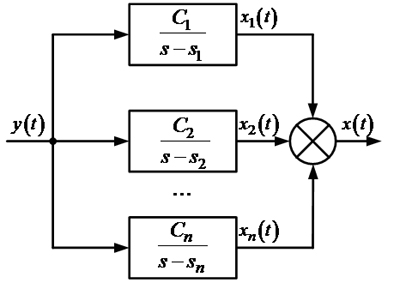
Рис. 3. Параллельная структура ПФ факторизованной формы.

Представления ПФ в виде последовательного или параллельного соединения простейших элементарных звеньев зачастую упрощает анализ и синтез САУ. Обратное преобразование Лапласа от простых дробей имеет табличную форму, что позволяет легко находить временные характеристики САУ любой сложности. Кроме того, эта форма записи ПФ обеспечивает переход к ММ в пространстве состояний канонической формы с диагональной матрицей состояния со всеми вытекающими из этого преимуществами (независимость переменных состояний друг от друга, простота обращения матрицы, удобство решения задач анализа и синтеза).

Хотя переход к ПФ канонической формы и связан с вычислениями, однако параметры ПФ канонической формы несут более богатую информацию о свойствах системы. Действительно, для линейных систем значения полюсов передаточной функции позволяют не только судить о необходимых условиях устойчивости, но и определяют достаточные условия устойчивости системы в целом, в полной мере отражают свойства САУ, позволяют сравнительно просто определять характер переходных процессов в системе.

Вместе с тем, параметры ПФ в канонической форме не в полной мере отражают физический смысл. Коэффициент пропорциональности здесь не имеет никакого физического смысла.

Сочетание достоинств стандартной и канонической форм записи ПФ достигается представлением передаточных функций в стандартно-факторизованной форме

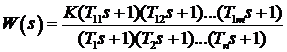(7)

Передаточная функция стандартно-факторизованной формы (7) объединяет удобство анализа и синтеза САУ, структурированность их ММ с ясным физическим смыслом параметров ПФ (статический коэффициент передачи отражает степень преобразования входного воздействия в выходную переменную САУ в статическом режиме, а постоянные времени характеризуют быстродействие или время протекания переходных процессов в отдельных элементах системы).

Поступила в редакцию 29.06.2009 г.