Исследование классического решения одной
обратной краевой задачи для эволюционного уравнения четвертого порядка,
возникающей в гидроакустике стратифицированной жидкости
Искендеров
Низамеддин Ширин оглу,
доктор физико-математических наук,
профессор, декан механико-математического факультета,
Салимова
Гюльбахар Абдул гызы,
соискатель.
Бакинский государственный университет.
В работе исследована одна обратная
краевая задача для эволюционного уравнения четвёртого порядка, возникающего в
гидроакустике стратифицированной жидкости. Сначала исходная задача сводится к эквивалентной
задаче, для которой доказывается теорема существования и единственности
классического решения. Далее, пользуясь этими фактами, доказывается
существование и единственность классического решения исходной задачи.
Для уравнения [1, 2]
![]() (1)
(1)
в области ![]() рассмотрим обратную задачу при граничных условиях
рассмотрим обратную задачу при граничных условиях
![]() (2)
(2)
начальных условиях
![]()
![]() , (3)
, (3)
и дополнительном условии
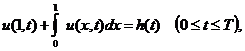 (4)
(4)
где ![]() -фиксированное число,
-фиксированное число, ![]() ,
, ![]() -заданные функции, а
-заданные функции, а ![]() и
и ![]() -искомые функции.
-искомые функции.
Примем следующее
Определение. Классическим решением задачи (1)-(4) назовём пару ![]() функций
функций ![]() и
и ![]() , обладающих следующими свойствами:
, обладающих следующими свойствами:
1) функция ![]() непрерывна в
непрерывна в ![]() вместе со всеми своими
производными, входящими в уравнение (1);
вместе со всеми своими
производными, входящими в уравнение (1);
2) функция ![]() непрерывна на
непрерывна на ![]() ;
;
3) все условия (1)-(4) удовлетворяются
в обычном смысле.
Справедлива следующая
Лемма 1. Пусть ![]() при
при ![]() ,
,
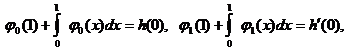
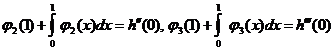 .
.
Тогда задача нахождения
классического решения задачи (1)-(4) эквивалентна задаче определения функций ![]() и
и ![]() , обладающих свойствами 1) и 2) определения классического
решения задачи (1)-(4), из (1)-(3) и
, обладающих свойствами 1) и 2) определения классического
решения задачи (1)-(4), из (1)-(3) и
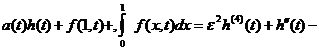
![]() (5)
(5)
С целью исследования задачи
(1)-(3), (5), рассмотрим следующие прос-транства. Обозначим через ![]()
![]() совокупность всех
функций вида
совокупность всех
функций вида
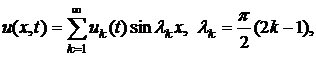
рассматриваемых в ![]() , где каждая из функций
, где каждая из функций ![]() непрерывна на
непрерывна на ![]() и
и
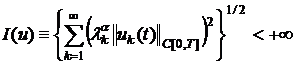 , (6)
, (6)
причём ![]() . Норму в этом множестве определим так:
. Норму в этом множестве определим так:
![]() .
.
Через ![]() обозначим пространство
обозначим пространство
![]() вектор-функций
вектор-функций ![]() с нормой
с нормой
![]() .
.
Известно, что ![]() и
и ![]() являются банаховыми
пространствами.
являются банаховыми
пространствами.
Первую компоненту ![]() решения
решения ![]() задачи (1)-(3), (5) будем искать в виде
задачи (1)-(3), (5) будем искать в виде
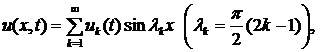 (7)
(7)
где
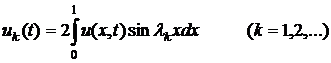 .
.
Тогда, применяя схему метода Фурье,
из (1) и (2), получаем:
![]() , (8)
, (8)
![]() (9)
(9)
где
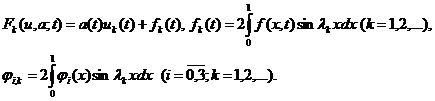
Теперь, из (5), с учетом (7),
имеем:
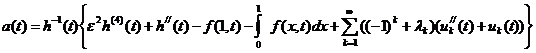 . (10)
. (10)
После применения метода вариации
постоянного решения задачи из (8) и (9) находим ![]() :
:
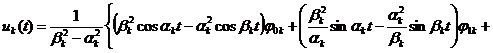
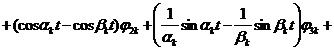
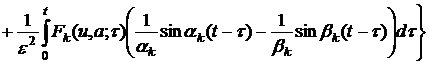 , (11)
, (11)
где 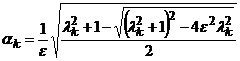 ,
, 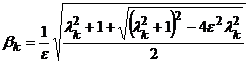 .
.
Подставляя ![]() из (11) в представление (7), получаем:
из (11) в представление (7), получаем:
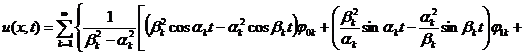
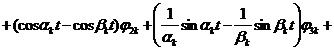
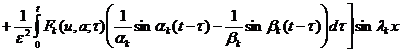 . (12)
. (12)
Теперь из (11) имеем:
![]()
![]()
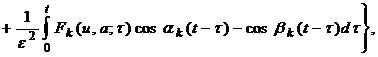 (13)
(13)
![]()
![]()
![]()
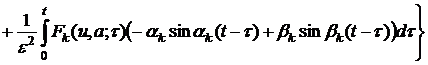 , (14)
, (14)
![]()
![]()
![]()
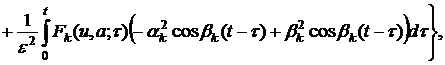 (15)
(15)
![]()
![]()
![]()
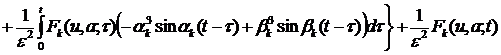 . (16)
. (16)
Далее, из (11) и (14) видно, что
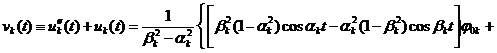
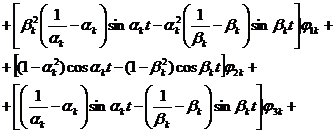
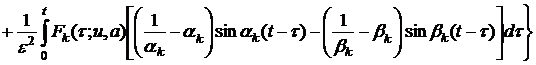 . (17)
. (17)
После подстановки выражения ![]() из (17) в (10), для
определения второй компоненты
из (17) в (10), для
определения второй компоненты ![]() решения задачи
(1)-(3), (5) находим:
решения задачи
(1)-(3), (5) находим:
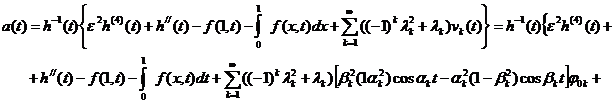
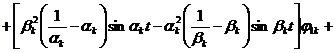
![]()
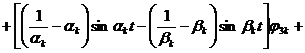
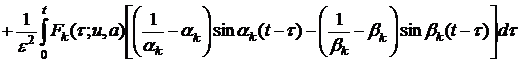 . (18)
. (18)
Исходя из определения решения
задачи (1)-(3),(5) доказывается следующая
Лемма 2. Если ![]() - любое решение задачи (1)-(3), (5), то функции
- любое решение задачи (1)-(3), (5), то функции
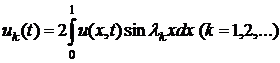
удовлетворяют на ![]() системе (11).
системе (11).
Нетрудно видеть, что
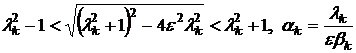 ,
,
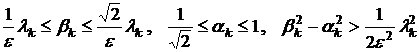 .
.
Теперь, из (11), (13)- (17),
соответственно имеем:
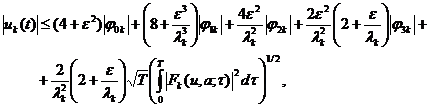
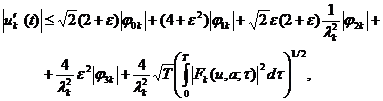
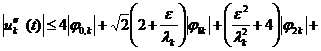
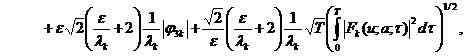
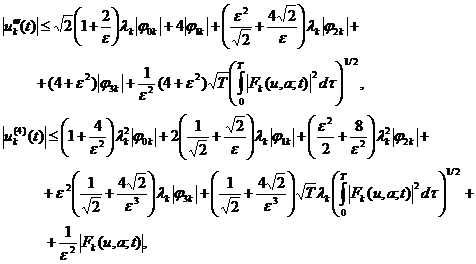
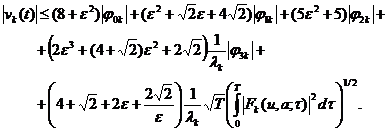
Отсюда имеем:
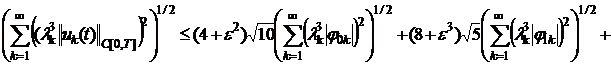
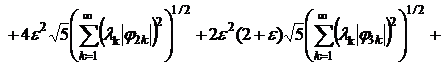
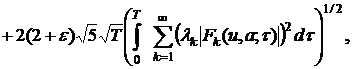 (19)
(19)
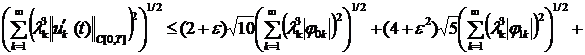
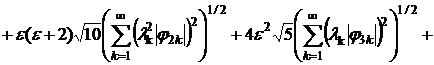
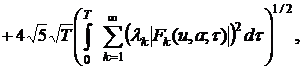 (20)
(20)
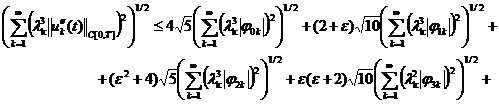
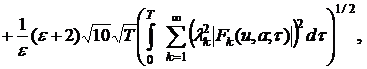 (21)
(21)
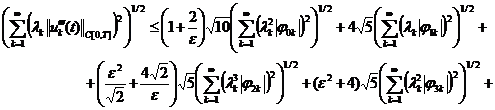
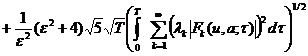 , (22)
, (22)
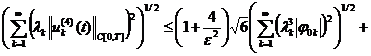
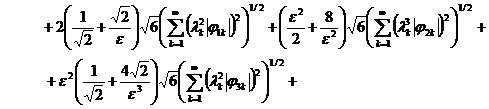
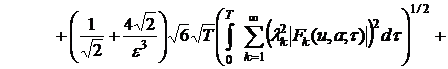
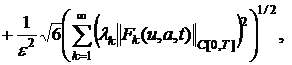 (23)
(23)
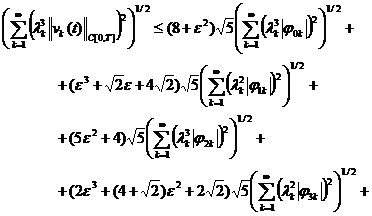
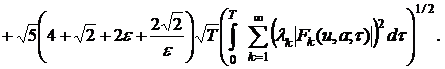 (24)
(24)
Предположим, что данные задачи
(1)-(3), (5) удовлетворяют следующим условиям:
![]() и
и ![]()
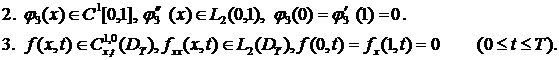
![]() при
при ![]() .
.
Тогда из (19)- (24), соответственно,
имеем:
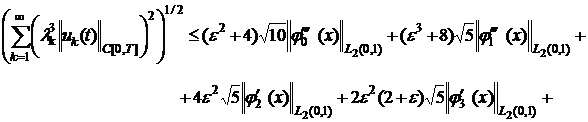
![]() (25)
(25)
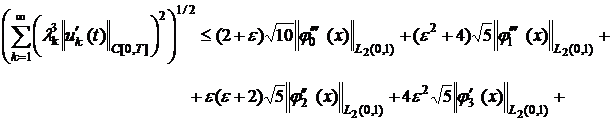
![]() (26)
(26)
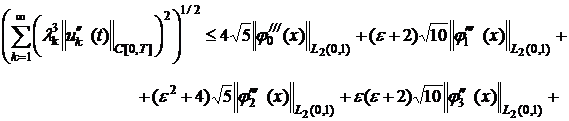
![]() (27)
(27)
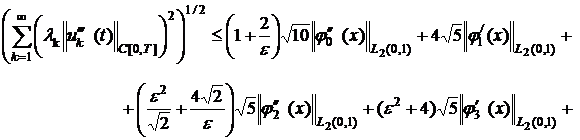
![]() (28)
(28)
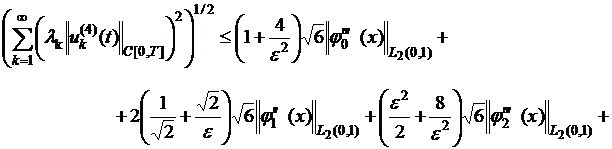
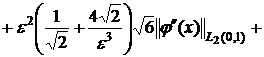
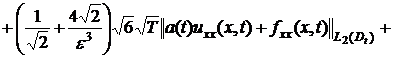
![]() (29)
(29)
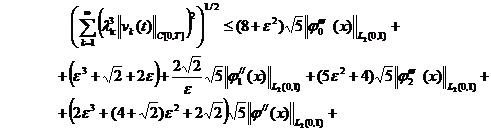
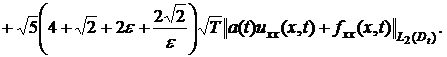 (30)
(30)
Далее, из (25) находим:
![]() (31)
(31)
где
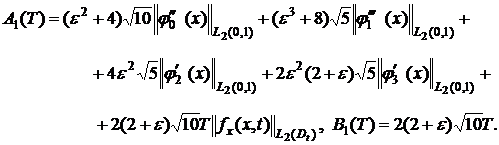
Теперь из (18), с учетом (30),
имеем:
![]() (32)
(32)
где
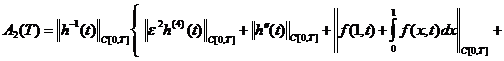
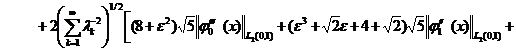
![]()
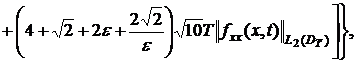
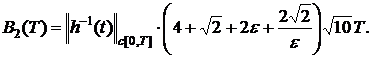
Из неравенств (31) и (32)
заключаем:
![]() (33)
(33)
где
![]()
Доказана следующая
Теорема 1. Пусть выполнены условия
1-4 и
![]() . (34)
. (34)
Тогда задача (1)-(3), (5) имеет в шаре ![]() из
из ![]() единственное решение.
единственное решение.
Доказательство. В пространстве ![]() рассмотрим уравнение
рассмотрим уравнение
![]() (35)
(35)
где ![]() , компоненты
, компоненты ![]() оператора
оператора ![]() определены правыми
частями уравнений (12),(18), соответственно.
определены правыми
частями уравнений (12),(18), соответственно.
Рассмотрим оператор ![]() в шаре
в шаре ![]() из
из ![]() . Аналогично (33) получаем, что для любых
. Аналогично (33) получаем, что для любых ![]() справедливы оценки.
справедливы оценки.
![]() (36)
(36)
![]() (37)
(37)
Тогда из оценок (36) и (37), с
учётом (34), следует, что оператор ![]() действует в шаре
действует в шаре ![]() и является сжимающим. Поэтому,
в шаре
и является сжимающим. Поэтому,
в шаре ![]() оператор
оператор ![]() имеет единственную
неподвижную точку
имеет единственную
неподвижную точку ![]() , которая является решением уравнения (35).
, которая является решением уравнения (35).
Функция ![]() , как элемент пространства
, как элемент пространства ![]() , непрерывна и имеет непрерывные производные
, непрерывна и имеет непрерывные производные ![]() .
.
Из неравенств (26)-(29) следует, что ![]() ,
, ![]()
![]() непрерывны в
непрерывны в ![]() . Далее, легко проверить, что уравнение (1) и условия (2),
(3), (5) удовлетворяются в обычном смысле. Значит,
. Далее, легко проверить, что уравнение (1) и условия (2),
(3), (5) удовлетворяются в обычном смысле. Значит, ![]() является решением
задачи (1)-(3), (5). А в силу леммы 2, это решение единственно в шаре. Теорема
доказана.
является решением
задачи (1)-(3), (5). А в силу леммы 2, это решение единственно в шаре. Теорема
доказана.
Таким образом, в силу леммы 1, справедлива
следующая
Теорема
2. Пусть выполнены все
условия теоремы 1 и
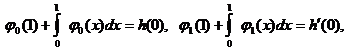
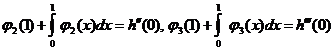 .
.
Тогда задача (1)-(4) имеет в шаре ![]() из
из ![]() единственное
классическое решение.
единственное
классическое решение.
Литература
1.
Габов
С.А., Малышева Г.Ю., Свешников А.Г. Об одном уравнении составного типа, связанном
с колебаниями сжимаемой стратифицированной жидкости. Дифференциальные
уравнения, 1983 ,т. 19, №7, с. 1171-1180.
2.
Габов
С.А., Оразов Б.Б., А.Г. Свешников. Об одном эволюционном уравнении четвёртого порядка,
возникающем в гидроакустике стратифицированной жидкости. Дифференциальные
уравнения, 1986, т. 22, № 1, с. 19-25.
3.
Худавердийев
К.И. К теории многомерных смешанных задач для нелинейных гиперболических
уравнений.-Дис.. док.физ.–мат.наук, Азгосуниверситет, - Баку, 1973.
4.
G.A.Salimova. On a boundary value problem for a fourth
order partial differential equation.Transactions of National Academy of Sciences
of Azerbaijan, series of physical technical and mathematical and mathematical
sciences, 2006, v. XXYI, 7,-pp. 125-138.
Поступила в
редакцию 15.04.2009 г.