Одна теорема о гомоморфизмах
групп и ее применение во взаимносвязном обучении математики
Бахшалиев Яфас Расул оглу,
кандидат
физико-математических наук, доцент,
зав. кафедрой алгебры и
теории чисел Азербайджанского государственного педагогического университета.
Начиная с 30-х годов XIX столетия, появились
новые направления в развитии математики, которые имели определяющую роль не
только в развитии самой математики, но и в развитии его преподавания. Так,
например, теория множества, неевклидовая геометрия, абстрактная алгебра и.т.д.
Интерес преподавания
математики появилось после того, как в 1972 в году Феликс Клейн выдвинул свою
знаменитую «Эрлагенскую программу». Клейн хотел оживить преподавание, выдвинув
в точных науках - в анализе, геометрии и физике - на первое место понятие
группы и идею преобразования. Цель математической теории – объединить и изучать
то, что инвариантно относительно некоторой группы преобразований. Эти инвариантные
элементы образуют ядро теории, которое часто называют «математической структурой»
[1, с. 228].
Идеи Ф. Клейна не
принимались однозначно в то время математиками. Некоторые считали, что Ф. Клейн
внес большой вклад в теорию групп, поэтому естественно преувеличивал до
некоторой степени роль понятия группы.
Дальнейшее развитие теории
групп и ее применение в различных областях, не только современной математики,
но и даже науки современного естествознания показали насколько точно определено
направление развития математической науки. Это программа также повлияла на
развитие преподавания математики на университетском уровне. В конце 40-х годах XX столетия появившиеся во
Франции математическое общество под названием «Бурбаки» определили новые
взгляды на саму науку математики и ее преподавание на всех уровнях обучения.
Эти идеи нашли отражение в бывших советских школах только после школьной
реформы 1969 года. Начиная с 1970-1971 учебного года, в учебном плане университетов
были введены элементы современной математики, в том числе элементы абстрактной
алгебры.
Тогда уже интенсивно
развивались алгебраизация как математических так и естественных наук. Этот
процесс продолжается и сейчас. Это можно показать на примере того, как теорема
о гомоморфизмах групп применяется во взаимосвязанности изложении теоретических
вопросов математики.
Пусть 
и 
некоторые группы с
одинаковым (или разными) основными бинарными операциями. Если 
гомоморфизм группы 
в (или на) группу 
(короче -
), то фиксируя 
получается уравнения
и металлические брекеты, элайнеры (каппы брекетыворонеж.рф
(1)
Решить уравнение (1)
–значит найти прообразы 
по заданному образу .
Вполне очевидно, что
если 
, т.е. если 
принадлежит образу
группы относительно , то существует хотя бы один прообраз (а может быть прообраз есть один класс). Известна из [2]:
Теорема. Если гомоморфизм группы в (или на) группы и если 
, тогда всякие решения уравнения (1) можно найти композицией
одного частного решения 
уравнения (1) на любое
решение уравнения
(
-нейтральный элемент) (2)
Доказательство этой
теоремы можно получить как следствие из основной теоремы о гомоморфизмах групп.
Но применения этой теоремы очень интересна.
1. Пусть задана система линейных алгебраических уравнений с
«
» неизвестными над любым полем P
P 
(3)
P 
При обозначенных
, 
, 
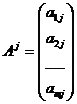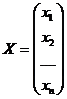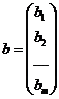
систему (3) можно
записать в следующей векторной форме:
(4)
и матричном виде
(5)
Легко показать, что
система (3) эквивалентна векторному уравнению (4) и матричному уравнению (5).
Однородная система ,
соответствующая системе (3) имеет вид:
(6)
векторная форма ее
записи имеет вид:
(7)
в матричном виде
(8)
Очевидно, что
отображение 
является гомоморфизмом
линейного пространства P n в P m и поэтому она является
гомоморфизмом аддитивных групп этих пространств:
< P n ; +> и < P m ;+>
Значит
A: < P n :+> ≃< P m ;+>
Поэтому можно применить
вышеприведенную теорему к системе уравнений (3) (или матричному уравнению (5).
Тогда имеем?
Предложение 1. Если в системе (3) вектор столбец «
» принадлежит линейной оболочке системе векторов 
, тогда всякие решения этой системы можно получить сложением одного
частного решения 
этой системы с всяким
решением соответствующей однородной системы (6) , т.е. 
, где 
.
При этом если основное
поле P является конечным полем характеристики «
» , то все сказанное остается в силе, только может меняться
измерение линейного многообразия порожденного решением этой системы.
2. Пусть задано двучленное уравнение над полем P
(
P *= P 
) (9)
Здесь рассматриваются
два случая:
а) P =
-поле комплексных чисел.
Тогда легко видеть, что 
является гомоморфизмом
на себя мультипликативной группы отличных от нуля комплексных чисел 
.
Поэтому имеем:
Предложение 2. Если в уравнении (9) 
, то все решения этого уравнения можно получить умножением
одного частного решения этого уравнения на
всевозможные корни уравнения
(10)
Пример. Найти все решения уравнения 
.
Одним частным решением этого
уравнения является 
; корнями же уравнения 
являются:
Тогда всеми решениями
заданного уравнения будут:
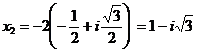
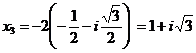
в) Если P конечное поле характеристики 
, то уравнение (9) не всегда разрешимо. В этом случае
мультипликативная группа поля P, т.е P * совпадает с циклической группой 
-го порядка, образующим элементом которого является один из
первообразных корней по модулю , т.е. 
Рассмотрим уравнение
(P *) (11)
Если рассмотреть
отображение , то очевидно, что оно отображает группу в себя и является
эндоморфизмом этой группы.
Для того, чтобы
уравнение (11) имело решение, необходимо и достаточно , чтобы 
. Так как циклическая, то 
тоже будет циклична и
будет иметь порядок 
, где 
–является делителем 
[2].
Если 
то «
» тоже будет иметь порядок ([3]).
Тогда имеем :
Предложение 3. Если в уравнении (11) 
и 
, то все решения этого уравнения можно получить умножением
одного частного решения на все решения
уравнения
Пример. Найти все решения уравнения 
над полем 
.
По условию 
и 
; те уравнение имеет решение.
Легко проверить, что 2
является первообразным корнем по модулю 
.
Легко проверить, что 
является решением
заданного уравнения, и 
являются всем
решениями уравнения 
.
Тогда решением заданного
уравнения будут:
; 
; 
; 
Литература
1. Р. Неванлинна. Реформа
в преподавании математики // На путях обновления школьного курса математики (сб.
статей и материалов). М., «Просвещение», 1980.
2. Р.Фор, А.Кофман, М.
Дени-пипен. Современная математика. М., «Мир», 1960.
3. С. Ленг. Алгебра. М.,
«Мир», 1968.
4. Н. Бурбаки. Очерки по
истории математики. М., Из-во «ИЛ», 1963.
5. Виленкин И.Я и др.
Современные основы школьного курса математики. М., «Просвещение», 1980.
6. Бахшалиев Я.Р. ,
Худавердиева Г.А. О связи курсов алгебры и теории чисел, геометрии и математического
анализа на математических факультетах педагогического института // Тезисы
всесоюзной научной конференции по проблемам межпредметных связей в подготовке
учителей математики и физики в пединститутах. Душанбе, 1978, с. 67-68.
7. Бахшалиев Я.Р.
Алгебраические структуры – основы взаимосвязного обучения математики // Доклады
Национальной Академии Азербайджана, 2007, № 6, с. 9-14.
Поступила
в редакцию 09.06.2009 г.