Автоматизированное управление процессом
прессования для производства ананасового сока
Экпеньонг Экпеньонг Экпо,
аспирант кафедры автоматизации
производственных процессов Кубанского государственного технологического
университета.
Основным регулируемым параметром
процесса прессования является давление пресса. Давление непосредственно зависит
от частоты вращения вала шнекового пресса. К процессу
прессования плодов ананаса предъявляются высокие требования по величине
давления, которая не должна значительно отличаться от оптимального давления,
обеспечивающего максимальное количество получаемого продукта.
Это накладывает жесткие
требования к системе автоматизации по обеспечению заданного давления в шнековом прессе и относительной степени затухания
переходного процесса на уровне 0,9 (практически неколебательного,
апериодического переходного процесса).
Нами была проведена
экспериментальная работа по определению динамических характеристик шнекового пресса, как объекта управления.
Безразмерная передаточная функция объекта по рассматриваемому каналу
без учета чистого запаздывания будет иметь вид:
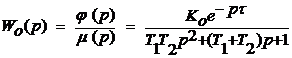 (1)
(1)
Здесь Ко
= 1,5 – безразмерный коэффициент усиления.
Разделение постоянных времени Т1 и Т2 проводится с
использованием номограммы в зависимости от отношения ![]() [1]. Как видно из
графика, Т1= 39 c, Т2 = 32 c. Кроме того, в объекте имеется чистое запаздывание
10 с.
[1]. Как видно из
графика, Т1= 39 c, Т2 = 32 c. Кроме того, в объекте имеется чистое запаздывание
10 с.
Определим коэффициент усиления по
данному каналу. Примем за базисное значение получаемого сока – величину ![]() гр
(50 процентов веса 1.5 килограммового плода).
гр
(50 процентов веса 1.5 килограммового плода).
Тогда относительное значение
изменения получаемого продукта при 10% входном воздействии равно:
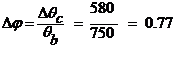 , следовательно,
, следовательно, 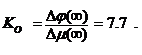
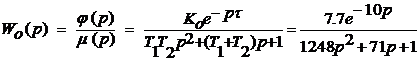 . (2)
. (2)
Оптимизация
параметров системы стабилизации давления при производстве ананасового сока
Поставляемые вместе с
оборудованием системы стабилизации давления в шнековом
прессе имеют в качестве исполнительного механизма сервомотор постоянной скорости
со временем полного хода регулирующего органа 100 с.
Сервомотор постоянной скорости
является нелинейным звеном, которое может быть заменено интегральным, если он
работает в скользящем режиме. Однако, если необходимо
определить параметры автоколебаний в замкнутой системе, то необходимо рассматривать
две нелинейности.
Известны методы линеаризации
статических нелинейностей релейного типа [3], но отсутствует методика
линеаризации двух последовательно включенных нелинейностей: реле – сервомотор
постоянной скорости. Для определения возможности использования двухпозиционного
регулятора необходимо их линеаризовать.
При разработке и исследовании реальных систем управления часто
приходится иметь дело с системами, использующими релейные элементы, управляющие
сервомоторами постоянной скорости. Такие сочетания встречаются при
использовании электронных регуляторов, в цифровых системах, реализующих
широтно-импульсную модуляцию с помощью выходных триггеров.
Мы предлагаем использовать метод
гармонической линеаризации одновременно двух нелинейностей [2, 5].
Последовательное включение реле и сервомотора постоянной скорости - явление
очень распространенное, поэтому метод также должен
получить распространение, хотя нами используется для конкретного применения в
системах автоматического управления с сервомотором постоянной скорости перемещения
регулирующего органа.
Под коэффициентом передачи пары нелинейностей будем
понимать отношение площадей сигналов на выходе и входе при подаче на вход
гармонического сигнала с амплитудой А. Тогда площадь входного сигнала за
половину периода будет равна:
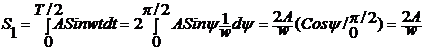 . (3)
. (3)
где ![]()
Сервомотор включается, если
входной сигнал реле больше зоны нечувствительности [2], x >![]() , где x
= A Sin wt.
, где x
= A Sin wt.
Таким образом, общая площадь
выходного сигнала за полупериод будет равна:
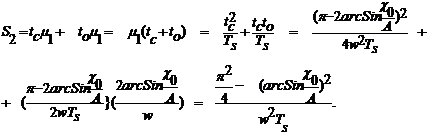
Частотная характеристика системы
нелинейностей может быть записана так:
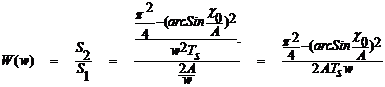 . (4)
. (4)
Имея передаточную функцию
нелинейностей, легко найти передаточную функцию всей линеаризованной системы и
определить ее частотные характеристики, исследовать на наличие автоколебаний, а
также определять их параметры
Расчет
параметров автоколебаний в системе стабилизации давления в шнековом
прессе при использовании релейного регулятора
Выясним возможность использования
метода обобщенной линеаризации двух нелинейностей [2, 3]. Для этого найдем
параметры автоколебаний с учетом обобщенной линеаризации.
![]()
Для вычисления параметров
автоколебаний следует приравнять вещественные и мнимые части АФХ объекта и
обобщенной линеаризованной функции, что приводит к необходимости решения
системы уравнений, записанных ниже.
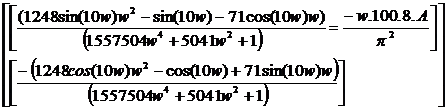
Решение полученной системы
уравнений дает: амплитуда автоколебаний Ао = 0,344,
частота автоколебаний Wo = 0,022 рад/с..
Проведем исследование параметров
автоколебаний по методу Гольдфарба. Для релейного элемента общего вида имеем:
![]() ,
, 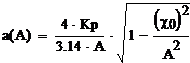 ,
, 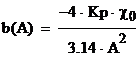 ,
,
где a(A)
и b(A) – коэффициенты гармонической линеаризации.
Амплитудно-фазовая характеристики линейной части при отсутствии
сервомотора постоянной скорости
![]()
Найдем параметры автоколебаний
при использовании идеального трехпозиционного релейного элемента [6].
Поскольку аналитического решения
уравнения: W(i,w) = J(a) нет,
то его можно решить графоаналитическим методом.
Для случая замены сервомотора соленойдным клапаном:
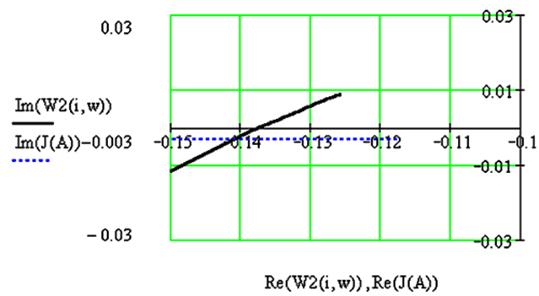
Рис. 1. Поиск точки пересечения W2(i,w)) и J(A).
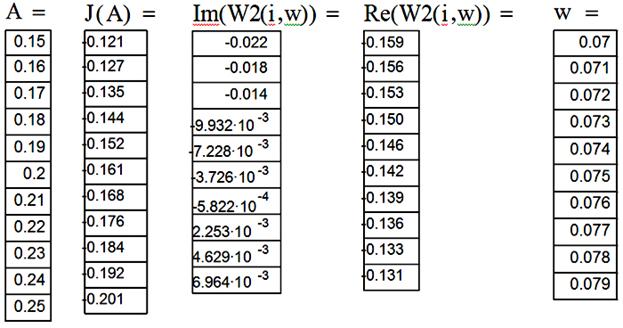
Параметры автоколебаний:
амплитуда автоколебаний Ao = 0.17, частота ![]() рад/с.
рад/с.
Таким образом, убрав сервомотор
постоянной скорости, можно уменьшить амплитуду автоколебаний почти в два раза.
Однако в обоих случаях амплитуда автоколебаний не допустима.
Расчет
оптимальных параметров регулятора в системе стабилизации давления в шнековом прессе при использовании существующего регулятора
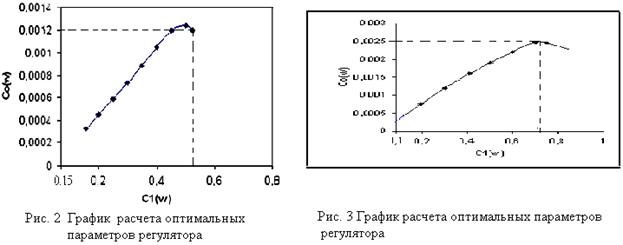
Проведем
оптимизацию по двум критериям: требуемой относительной степени затухания и минимуму
интеграла от модуля ошибки управления [1, 4].
Система автоматического
управления будет обладать требуемой относительной степенью затухания, если
расширенная амплитудно-фазовая характеристика разомкнутой система
автоматического управления будет проходить через точку на комплексной плоскости
(-1, j0).
![]() ,
, 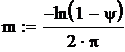 ,
, ![]() ,
,
![]()
Для регулятора со связанными
параметрами настройки обозначим:
![]() ,
,
![]() ,
,
где Re(Wob(I,w)) и Im(Wob(I,w)) – вещественная и
мнимая части обратной расширенной АФХ [4].
Оптимальными являются: ![]()
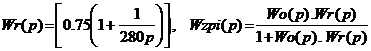
Поскольку в системе
управления присутствует звено чистого запаздывания, то переходный процесс
построим по обобщенной вещественной частотной характеристике.
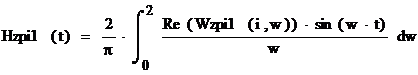 .
.
Исследования показали, что для
относительной степени затухания ![]() переходный
процесс имеет большой динамический заброс и высокую длительность переходного
процесса.
переходный
процесс имеет большой динамический заброс и высокую длительность переходного
процесса.
Увеличим ![]() . Проводя аналогичные расчеты, получили: Kp = 0,52, Ti = 364 c.
. Проводя аналогичные расчеты, получили: Kp = 0,52, Ti = 364 c.
Построив
переходную функцию замкнутой САУ по новой обобщенной вещественной характеристике
и выражению, приведенному ниже, сравним их.
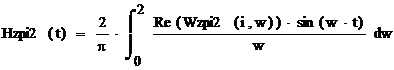
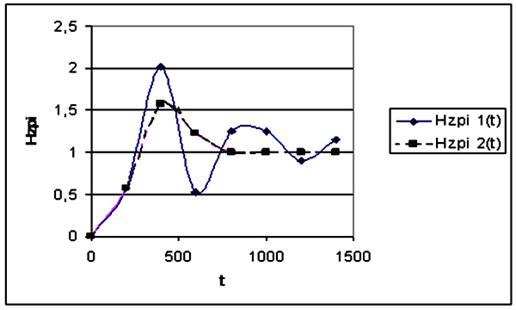
Рис. 4. Графики переходную функцию замкнутой
САУ.
Таким образом, увеличение
относительной степени затухания переходного процесса привело к снижению
динамического заброса на 70 %, в 2 раза уменьшилось время переходного процесса.
Расчет
оптимальных параметров цифрового регулятора, работающего в комплекте с
сервомотором постоянной скорости
На регулирующем органе установлен
исполнительный механизм постоянной скорости с постоянной времени сервомотора
100 с. Отнесем его к объекту.
Оптимальными будем считать
параметры цифрового регулятора, обеспечивающие относительную степень затухания ![]() = 0,99.
= 0,99.
![]() ,
, ![]() ,
, ![]() ,
,
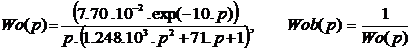
При оптимизации параметров
пропорционального регулятора необходимо найти: - Re(Wob(I,w)) = Kp. Задача решается графическим способом.
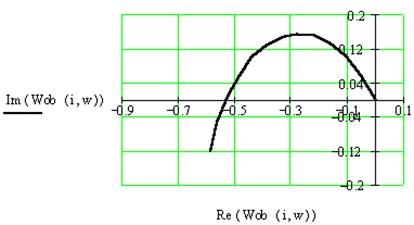
Рис. 5 График расчета оптимальных параметров
цифрового регулятора
Определение оптимального значения Кр.
Kpp : = 0.534
![]() ,
,
![]()
![]()
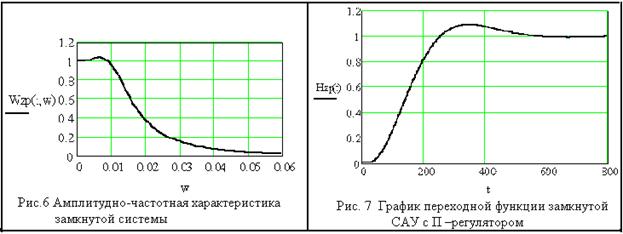
![]()
Частота пропускания замкнутой САУ при (3%)А(0) 0.054 рад/с.,
период квантования цифрового регулятора
следует брать не более
Tк =29.1 с.
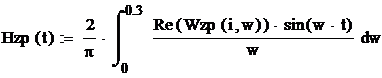
Как
следует из графика переходной функции, П – закон
управления дает желаемую динамику системы.
Динамика
цифровой системы управления всегда хуже динамики непрерывной. Проверим возможность
использования цифровой системы с П – законом
управления и сервомотором постоянной скорости. Для этого сравним переходные
функции замкнутых систем с непрерывным и цифровым управлением.
Получение передаточной функции приведенной
непрерывной части цифровой САУ
При анализе цифровых систем
управления их представляют в виде трех элементов: цифрового фильтра
(регулятора), фиксатора и приведенной непрерывной части [6].
Так как в системе имеет мести
фиксатор нулевого порядка с передаточной функцией вида:
![]() ,
,
то с учетом того, что z = e pT
, эту функцию можно записать в следующем далее виде:
![]() .
.
Сомножитель 1/р относят к линейной части, поэтому передаточная
функция приведенной непрерывной части может быть записана в следующем виде:
![]() .
.
Так как
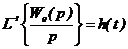 ,
,
есть переходная функция линейной
части системы, то z – передаточную функцию линейной
части находим по следующему выражению:
![]()
Результирующая передаточная
функция приведенной непрерывной части для периода квантования равного 10 с. получена ниже.
![]()
![]()
Для получения решетчатой
функции произведем замену t = nT.,
T := 10.
![]()
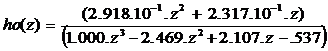 .
.
![]() .
.
Результирующая дискретная
передаточная функция приведенной непрерывной части:
![]()
Проверка правильности расчета
дискретной передаточной функции приведенной непрерывной части:
![]()
Поскольку предел равен
коэффициенту усиления объекта, то можно утверждать, что передаточная функция получена верно.
Кр = 0,534, Тс = 100 с.
Передаточная функция
пропорционального регулятора с учетом сервомотора постоянной скорости равна:
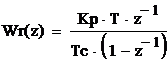 ,
, 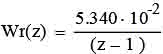 ,
, ![]() .
.
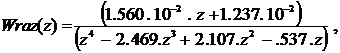
![]()
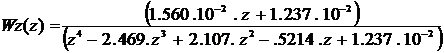
Расчет цифровой системы на
устойчивость по критерию Джури заключается в следующем.
Пусть задан А(z) –
характеристический полином:
A(z) = a0zn
+ a1n-1 + … + an, a0 > 0.
Введем понятие обратного полинома, получаемого перестановкой коэффициентов
исходного в обратном порядке: A(z) = anzn + an-1n-1 + …+ a0.
Разделим A(z) на обратный
ему. В итоге получаем частное от деления число Q(1) и остаток А1(z) – полином n-1 степени.
Домножим полученный результат на z-1 получаем:
A1(z) = (a0-anq0)zn-1
+ … + (an-1-a1q0).
Затем делим остаток A1(z) на обратный ему A10(z)
и определяем новое q1 и A2(z)
![]() и т.д.
и т.д.
Выполняя деление полиномов Ai(z) на обратные ему Ai0(z),
получаем последовательность чисел Qi = {Q(1),Q(2),…Q(n-1)}.
Необходимым и достаточным условием
устойчивости цифровой системы является неравенства:
S1
= A(1) = (a0 + a1 + a2 +…+
an) > 0;
S2
= (-1)nА(-1) = (a0(-1)n + a1(-1)n-1
+…+ an) > 0;
|Q(i)| < 1, i = 1,2,…,n-1.
![]()
Цифровая система устойчива,
поскольку выполняются все три необходимых условия:.
![]()
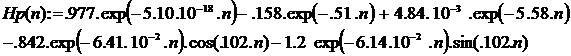
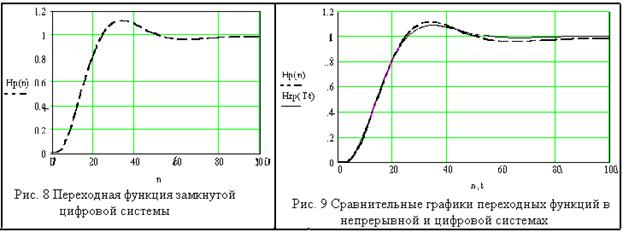
Как следует из графика переходной
функции, динамика замкнутой системы с цифровым П -
регулятором практически не отличается от динамики непрерывной системы с П-
регулятором.
Таким образом, целесообразно исключить интегральную составляющую регулятора,
что существенно улучшит динамику замкнутой системы. Расчет оптимальных параметров
регулятора в системе стабилизации давления в шнековом
прессе при использовании существующего регулятора показано, что увеличение
относительной степени затухания переходного процесса приводит к снижению
динамического заброса на 70 %, и к тому что в 2 раза
уменьшается время переходного процесса.
Рассчитаны оптимальные параметры
цифрового регулятора, работающего в комплекте с сервомотором постоянной
скорости. В связи с тем, что динамика замкнутой системы с цифровым П - регулятором практически не отличается от динамики
непрерывной системы с П- регулятором и полностью удовлетворяет требованиям к
системе, целесообразно исключить интегральную составляющую регулятора, что
существенно улучшит динамику замкнутой системы.
Литература
1. Балакирев
В.С. и др. Экспериментальное определение динамических характеристик промышленных
объектов управления. М: Энергия, 1967. -232 с.
2. Изерман
Р. Цифровые системы управления. М.:Мир,1984. -541 c.
3. Пугачев В.И. Нелинейные и
цифровые системы управления. Методические указания по курсу «Теория
автоматического управления», Часть
4. Пугачев В.И. Теория
автоматического управления, раздел Цифровые системы управления. Учебное
пособие, типография «Мир Кубани», г. Краснодар, 2005. -100 с.
5. Стефани
Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов. - М.:Энергия, 1972. -376 с.
6. Цыпкин
Я.З. Релейные автоматические системы.-М.:Наука,
1974. -575 c.
Поступила
в редакцию 30.07.2009 г.