Исследование кондуктивного теплообмена в
вынужденных потоках жидкостей с переменными теплофизическими свойствами в
условиях активных термических участков
Койбагаров Самат Хариевич,
кандидат технических наук, и.о. доцента кафедры
техической физики и теплоэнергетики Семипалатинского государственного
университета им. Шакарима.
При изотермическом течении
реальных жидкостей в условиях, характерных для теплообменников с малой
относительной длиной обогреваемых участков (l/d
< 50), и наличии достаточных температурных напоров возможно развитие
термогидродинамических процессов, способных привести к существенному перерождению
форм движения [1-5]. Эти явления наиболее интенсивны в пристеночном слое
начальных термических участков, где наблюдаются максимальные градиенты
температур, вызывающие значительные изменения теплофизических характеристик
вихревых потоков многокомпонентной жироэмульсионной смеси мясокостного сырья
при термообработке в теплообменном аппарате для извлечения жира.
В указанных условиях
практически не исследовались процессы переноса в потоках жидкостей с большими
значениями вязкости, хотя именно в таких средах возникают наиболее
благоприятные условия для развития неустойчивости течения. При малых скоростях
движения жидкостей (Rе<2300) в теплообменном
аппарате, выполненном из материалов,
обладающих относительно высокой теплопроводностью ![]() , процессы кондуктивного переноса тепла в вихревом потоке
существенно зависят от интенсивности распространения тепла в стенке аппарата. В
связи с этим при решении задач, связанных с кондуктивным теплообменом в
системах указанной физической структуры, необходимо совместное рассмотрение
уравнений распространения тепла в стенке и в жидкости вместе с уравнениями
движения, т.е. решения сопряженной задачи.
, процессы кондуктивного переноса тепла в вихревом потоке
существенно зависят от интенсивности распространения тепла в стенке аппарата. В
связи с этим при решении задач, связанных с кондуктивным теплообменом в
системах указанной физической структуры, необходимо совместное рассмотрение
уравнений распространения тепла в стенке и в жидкости вместе с уравнениями
движения, т.е. решения сопряженной задачи.
При математическом описании
стационарного теплообмена при течении потока в вертикальном круглом варочном
котле приняты следующие допущения:
1)
перенос тепла вдоль оси цилиндрического аппарата за
счет теплопроводности в потоках капельных жидкостей мал по сравнении с переносом
тепла конвекцией (при Ре > 100);
2)
радиальный градиент давления мал по сравнении с осевым;
3)
вторые производные осевой скорости и температуры в
осевом направлении намного меньше, чем в радиальном и ими можно пренебречь;
4)
температуры стенки и потока постоянны и имеют равномерное распределение
по сечению;
5)
профиль скорости по сечению аппарата является развитым (параболическим);
6)
плотность теплового потока на участке активного нагрева постоянна;
7)
в потоке отсутствуют внутренние источники тепла, теплота трения пренебрежимо
мала;
8)
теплопотери в окружающую среду отсутствуют.
С учетом указанных допущений задача
описывается системой дифференциальных уравнений:
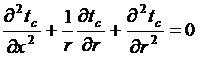 (1)
(1)
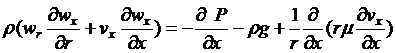 (2)
(2)
![]() (3)
(3)
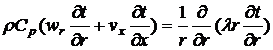 (4)
(4)
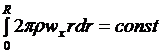 (5)
(5)
Зависимости физических
свойств аппроксимируются следующими соотношениями:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
Решение системы определялось
при следующих граничных условиях:
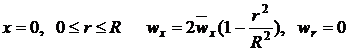 (10)
(10)
![]()
![]() (11)
(11)
![]() (12)
(12)
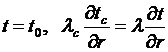
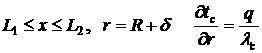 (13)
(13)
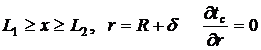 (14)
(14)
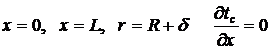 (15)
(15)
Структура исходных уравнений
(1)-(9) предопределяет возможность, решения задачи только численным методом.
Анализ известных решений задач кондуктивното тепломассопереноса (2)-(4)
показывает, что для принятой формулировки условий необходимо дополнительно
учитывать влияние стенки аппарата; при выборе алгоритма решении следует
обеспечить исключение неустойчивости при больших значениях wr (в отличие от (2)).
Численный алгоритм, приведенный d (3) хотя и допускает возможность решения системы
(2)-(4) в полном объеме, однако его реализация связана с использованием разреженных
матриц высокого порядка, что ухудшает точность решения из-за вынужденного
уменьшения используемого числа узлов по радиусу.
Трудность численного решения
поставленной задачи определяется необходимостью обеспечения
связи уравнения теплопроводности стенки теплообменного аппарата с
уравнениями переноса для потока (2)-(5), что требует реализации граничных
условий IV рода на границе жидкость – стенка. Итерации по стыковке температурных
полей на внутренней поверхности стенки и внешней поверхности потока осуществляются
при пограничных условиях I рода со стороны стенки и II рода со стороны потока.
Подобный подход моделирует процесс разогрева стенки при мгновенном
устанавливающемся ее температурном поле. Для совместного решения системы
уравнений (1)-(4) с интегральным уравнением материального баланса (5) применена
схема расщепления уравнения переноса импульса (4).
Численные расчеты
проводились с целью оценки влияния основных параметров определяющих условия теплопереноса
(скорости вращения потока, диаметра аппарата, объема обогреваемого участка, мощности
нагревателя), на развитие процессов для группы органических жидкостей
(жироэмульсии мясокостного сырья). Полученные данные о распределении профилей
скоростей (wx ,wr) и температур (t, tc) по оси и радиусу
позволяют оценить характер их
деформаций по мере прохождения потоком измерительного участка. Перестройка wx и ,wr , вызываемая наличием максимальных градиентов температур, а также
перемежаемости профилей температур в пристеночном слое, определяемых резким
изменением характера распределения тепла в области 2 < Х < 4 и существенной зависимостью теплофизических свойств жидкостей
от температуры, являются причинами развития процессов
неустойчивости изменений вязкости. Результаты расчета среднеинтегральных
температур внешней поверхности стенки достоверно отражают изменения теплофизических
свойств исследованных жидкостей от состава, концентрации или скорости потока,
что доказывает пригодность предложенной модели для расчета статических характеристик
преобразователей, предназначенных для измерения соответствующих параметров
потока. Погрешность расчета оценивалась по балансу тепловой энергии,
рассчитываемой по величине интегрального количества тепла в области с установившимся
теплообменом, и в исследованном диапазоне изменения параметров не превышала
0,01%.
Экспериментально установлена
адекватность модели реальным физическим процессам. Относительная погрешность
расчета не превышает 4,5%.
Получаемая
информация позволяет рассчитывать практически любые термогидродинамические характеристики
рассматриваемой модели. Результаты исследований позволяют рекомендовать
предложенную математическую модель для исследования аналогичных задач,
связанных с расчетом кондуктивного теплообмена в вынужденных вращающихся
потоках жидкостей с переменными свойствами в условиях существенной изотермичности,
характерной для малых участков активного нагрева многокомпонентной жироэмульсионной
смеси мясокостного сырья при термообработке в теплообменном аппарате для
извлечения жира.
Обозначения:
x, r – осевая и радиальная
координаты соответственно; R, d -
радиус и толщина стенки аппарата; wx
,wr - осевая и радиальная
составляющие скорости; tc-
температура стенки; t0, t - начальное и текущие значения
температуры стенки; Р0 , Р - начальное и текущее значение давления; ![]() - среднее значение
скорости; q- удельный тепловой поток; Q - мощность электрического нагревателя аппарата; m - коэффициент динамической
вязкости; l, lc - коэффициенты
теплопроводности жидкости и стенки; Ср -
удельная теплоемкость; r -плотность;
b1, b2, bl, bCP, br - коэффициенты
температурных завиcимостей физических свойств потока; VH -
объем обогреваемого потока; L, L1, L2 - длина измерительного,
предвключенного и участка за нагревателем (L=5VH); X=x/VH - безразмерная величина;
- среднее значение
скорости; q- удельный тепловой поток; Q - мощность электрического нагревателя аппарата; m - коэффициент динамической
вязкости; l, lc - коэффициенты
теплопроводности жидкости и стенки; Ср -
удельная теплоемкость; r -плотность;
b1, b2, bl, bCP, br - коэффициенты
температурных завиcимостей физических свойств потока; VH -
объем обогреваемого потока; L, L1, L2 - длина измерительного,
предвключенного и участка за нагревателем (L=5VH); X=x/VH - безразмерная величина; ![]() - среднеинтегральная
температура.
- среднеинтегральная
температура.
Литература
1.
Берман Л. Д. О критериях подобия
для совместно протекающих процессов тепло- и массообмена
в герерогенных системах.- Журнал технической физики. 1958. т. 28, вып. 11, с.
2617- 2629.
2.
Грачев Ю. П., Тубольцев В. К. Моделирование и опримизация тепло - и массообменных
процессов поизводств М.: Легкая и пищевая промышленность, 1982. – 296 с.
3.
Крейц Ф. Конвективный теплообмен во вращающихся системах. - В. кн.:
Успехи теплопередачи: Пер. с англ. - М.: Мир, 1971, с. 144 – 279.
4.
Лыков А. В. Явления переноса в капиллярно-пористых телах. – М., Госэнергоиздат,
1963. – 535с.
5.
Кутателадзе С. С. Теплопередача и
гидродинамическое сопротивление. М.. Энергоатом и здат, 1990.-367 с.
Поступила в
редакцию 23.11.2010 г.