Применение искусственных нейронных сетей для прогнозирования

Колмыков Вячеслав Викторович,

аспирант Мордовского государственного университета им. Н. П. Огарева,

инженер – программист ЗАО НТЦ «Модуль».

Решается задача обзора методов оконного прогнозирования на объеме страховых взносов. Рассматриваются методы одношагового и многошагового прогнозирования.

Введение

В настоящее время стала актуальной проблемой прогнозирования в страховом бизнесе. Поэтому в статье рассматриваются два метода прогнозирования. Основной задачей является выбор одного из метода прогнозирования на объемах страховых продаж.

Метод окон предполагает использование двух окон Wi и Wo с фиксированными размерами n и m соответственно. Эти окна способны перемещаться с некоторым шагом по временной последовательности исторических данных, начиная с первого элемента, и предназначены для доступа к данным временного ряда, причем первое окно Wi, получив такие данные, передает их на вход нейронной сети, а второе - Wo - на выход. Получающаяся на каждом шаге пара Wi -> Wo используется как элемент обучающей выборки (распознаваемый образ, или наблюдение).

Метод окон использует одношаговое и многошаговое прогнозирование.

Одношаговое прогнозирование.

Задача одношагового прогнозирования сводится к задаче отображения, когда один входной вектор отображается в выходной (рисунок 1).

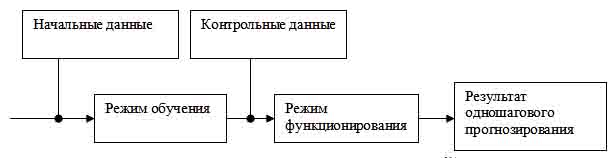
Рис. 1. Последовательность использования нейросети для задач одношагового прогнозирования.

Множество данных для однопараметрической задачи в таблице 1.

Таблица 1.

Множество данных для однопараметрической задачи.

Многошаговое прогнозирование.

Характеризуется увеличением дискретных отсчетов выходной величины и, соответственно, увеличением времени, на который осуществляется прогноз (время опережения Т_оп). При многошаговом прогнозировании Т_оп=а*R, где R - количество шагов вычисления прогнозирования; а - шаг дискретизации выходного параметра (например, год, месяц, день, и т.п.).

Многошаговое прогнозирование применяют лишь для явлений, признаки которых представлены в виде временных рядов.

Многошаговое прогнозирование временного ряда осуществляется следующим образом (рисунок 2). На входы нейросети подается вектор известных значень x(t_n-2), x(t_n-1), x(t_n). На выходе формируется прогнозируемая величина x*(t_n+1), которая определяет вектор прогнозируемых выходов и одновременно добавляется к значениям обучающего множества, то есть, принимается как достоверная. Далее на входы подается вектор x(t_n-1), x(t_n), x*(t_n+1), а на выходе получается x*(t_n+2) и следующие прогнозируемые значения.

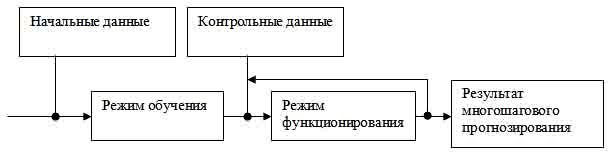
Рис. 2. Последовательность использования нейросетей для задач многошагового прогнозирования.

Многошаговое прогнозирование позволяет делать коротко- и среднесрочные прогнозы, поскольку существенное влияние на точность имеет накопление погрешности на каждом шаге прогнозирования. При применении долгосрочного многошагового прогнозирования наблюдается характерное для многих прогнозирующих систем постепенное затухание процесса, фазовые сдвиги и другие искажения картины прогноза. Такой тип прогнозирования подходит для стационарных временных рядов с небольшой случайной составляющей.

Прогнозирование с переобучением (рисунок 3) позволяет при больших интервалах опережения устранить затухание прогностических свойств сети за счет постоянного корректирования весовых коэффициентов синаптических связей.

На входы сети в режиме функционирования поступает последняя реализация обучающего множества x(t_n-2), x(t_n-1), x(t_n). Прогнозируемое значение выхода x*(t_n+1) откладывается в векторе прогнозируемых выходных значений и в качестве достоверного прибавляется к реальным значениям обучающего множества. Обучающее множество увеличивается на одно временное окно. Происходит процесс переобучения сети на увеличенном обучающем множестве, во время которого определяются новые весовые коэффициенты k синаптических связей и полиномов передаточных функций нейронов.

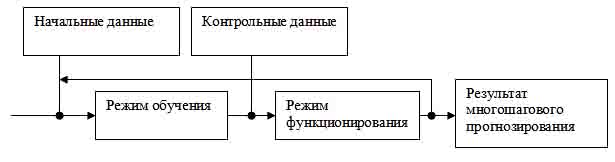
Рис. 3. Последовательность использования нейросети для задач многошагового прогнозирования

с переобучением.

Отметим, что алгоритм многошагового прогнозирования с переобучением сети для традиционных сетей прямого распространения с итерационным обучением является практически невыполнимым через большие временные задержки, необходимые на перенастраивание коэффициентов сети [1].

На основе выше изложенного материала удобно использовать, как метод одношагового, так и многошагового прогнозирования. Недостатком метода многошагового прогнозирования является, невыполнение через большие промежутки времени. И не маловажным фактором является, то какие значения имеются у нас на входе, и что мы хотим получить на выходе. Например, у нас на вход нейросети подаются данные о премиях и убытках страховой компании (таблица 2), на выходе мы хотим получить величину, относящуюся к премии.

Таблица 2.

Данные о ежемесячных продажах.

С помощью метода окон для нейронной сети будет сгенерирована обучающая выборка (таблица 3):

Таблица 3.

Обучающая выборка.

На выходе же мы получим прогноз страхового взноса на следующий период.

Показанный режим является одношаговым, что работает в режиме отображения (реальный вход - прогнозируемый выход).

Заключение

В данной статье рассматривались методы прогнозирования нейронных сетей. Нельзя сказать однозначно, какой из методов наиболее удобен. Выбор метода прогнозирования зависит от решаемой задачи. От факторов, влияющих на данную систему.

Литература

1.                  http://www.victoria.lviv.ua/html/oio/html/theme8_rus.htm#adaptacija. Тема 8. Нейросети в задачах отображения.

Поступила в редакцию 29.06.2010 г.