Метод межлабораторного сравнения в области измерения массы

 

Иванова Татьяна Александровна

докторант Рижского технического университета, Факультета транспорта и машиноведения, Института технологии машиностроения.

 

Введение

 

Впервые в Латвии с 2008 по 2009 год Латвийский центр Стандартизации, Аккредитации и Метрологии (SAMC) провёл межлабораторное сравнение в области измерения массы. Межлабораторное сравнение – это сличение и оценка полученных результатов между лабораториями. Целью проведения межлабораторного сравнения обычно является проверка способности выполнения точных измерений в лабораториях. В межлабораторном сравнении участвовало пять аккредитованных лабораторий в области измерения массы, включая пилотную лабораторию (SAMC). Пилотная лаборатория – это лаборатория, целью которой является проведение межлабораторного сравнения, а также определение референтного значения измеряемого объекта. Референтное значение – это значение, полученное в пилотной лаборатории, оно должно быть наиболее близким к истинному значению.

Целью работы является разработка метода проведения межлабораторного сравнения для контролирующих организаций. Для этого изначально были рассмотрены отчёты о проведении межлабораторного сравнения в Мексике, Швеции и Великобритании [9, 10, 11], а также международные руководящие документы. На основании этого был разработан метод межлабораторного сравнения, в котором была применена звездообразная маршрутная схема эталонов массы.

 

1. Метод межлабораторного сравнения.

 

Метод межлабораторного сравнения заключается в следующем:

1.                   Выбор измеряемого объекта и постановка задачи лабораториям-участницам.

2.                   Правила проведения межлабораторного сравнения.

3.                   Выбор схемы межлабораторного сравнения в зависимости от количества участников и от их географического расположения.

4.                   Оценка результатов, полученных при измерении эталонов массы в пилотной лаборатории.

5.                   Определение референтного значения эталона массы в пилотной лаборатории:

а)                   определение условной массы эталона,

б)                  оценка неопределённости условной массы эталона.

6.                   Анализ данных при сличении результатов пилотной лаборатории с результатами лабораторий участниц:

а)                   графическая оценка лабораторий – участниц,

б)                  аналитическая оценка лабораторий – участниц.

7.                   Исследование неопределённости и наилучшей способности измерения в лабораториях – участницах.

 

1.1. Выбор измеряемого объекта и постановка задачи лабораториям – участницам.

В качестве измеряемого объекта пилотной лабораторией были отобраны эталоны массы класса точности Е₁: (100 мг) и класса точности F₁ (1 г, 50 г, 100 г, 500 г, 1 кг, 20 кг). Пилотная лаборатория дала задание лабораториям-участницам определить условную массу и неопределённость этих эталонов. Лаборатории-участницы могли использовать свои средства измерения (эталоны, весы, компараторы массы), свои лабораторные помещения, а также применять утверждённые процедуры и методы калибровки.

 

1.2. Правила, которые необходимо соблюдать при проведении межлабораторного сравнения.

В процессе межлабораторного сравнения необходимо соблюдать общие требования, которые относятся к разработке схемы, выбору персонала, выбору измеряемого объекта, транспортировке измеряемого объекта (в данном случае эталона массы), обработке результатов. Также большое внимание необходимо уделить конфиденциальности лабораторий и возможной фальсификации результатов измерений.

 

1.3. Выбор схемы межлабораторного сравнения в зависимости от количества участников и от их географического расположения.

Наиболее распространёнными маршрутными схемами измеряемых объектов являются схема типа «ромашка» и схема типа «звезда». Схема типа «ромашка» – это такая схема, когда измеряемый объект следует последовательно из пилотной лаборатории в первую лабораторию n₁, затем во вторую n₂, третью n₃, …n_i и возвращается обратно в пилотную лабораторию. Такую схему целесообразно применять при большом количестве участников. В связи с тем, что в данном случае количество участников небольшое (5 лабораторий, см. выше), пилотная лаборатория выбрала звездообразную схему маршрута эталонов массы. Преимущество этой схемы в том, что можно контролировать массу эталонов между лабораториями.

Пилотной лабораторией был составлен график проведения межлабораторного сравнения, который был согласован с участниками. В межлабораторном сравнении с применением звездообразной схемы участвовало 5 латвийских аккредитованных лабораторий в области измерения массы: «А», «B», «C», «D» и «PL» – пилотная лаборатория (рис. 1).

 

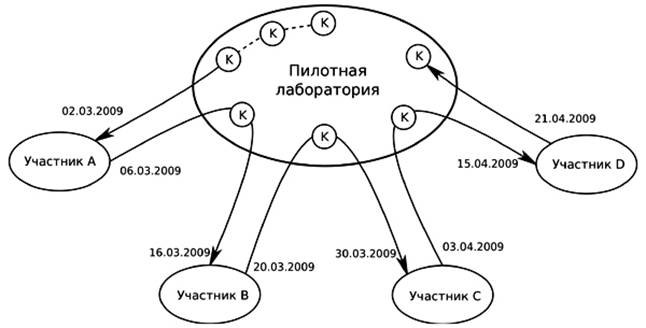
Рис. 1. Звездообразная схема маршрута эталонов массы.

 

1.4. Оценка результатов, полученных при измерении эталонов массы в пилотной лаборатории.

Перед тем, как распространять эталоны по лабораториям, эталоны массы были откалиброваны несколько раз в пилотной лаборатории на высокоточных компараторах массы. Калибровка осуществлялась путём сличения двух гирь, одна из которых была референтным эталоном, а вторая – тестируемым. В нашем случае тестируемыми эталонами являлись: 100 мг, 1 г, 50 г, 100 г, 500 г, 1 кг и 20 кг. Многократная калибровка была необходима для того, чтобы произвести оценку стабильности этих эталонов, а также определить их референтное значение, которое будет наиболее близким к истинному значению массы.

На рис. 2 в качестве примера отображены результаты калибровки, полученные в течение одного года для номинала 100 мг наивысшего класса точности Е₁.

 

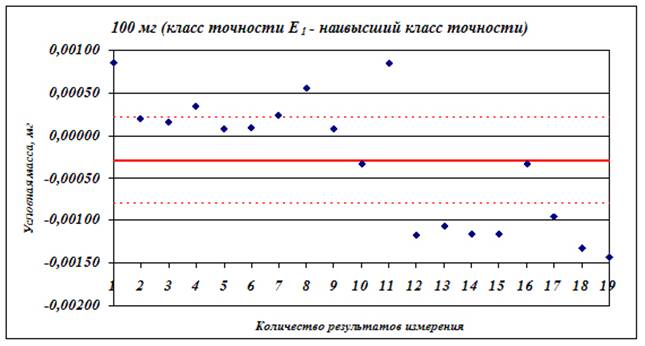
Рис. 2. Результаты калибровки и их фильтрация (доверительный интервал 99%).

 

На графике видно (рис. 2), что пилотная лаборатория получила довольно большой разброс результатов калибровки. Предположим, что некоторые результаты являются ошибочными, это может быть связано с низким качеством электропитания, потоками воздуха, толчками фундамента здания, в котором находятся компараторы массы. Но основной задачей пилотной лабораторией является определение референтного значения, которое должно быть близким к истинному значению.

 

1.5. Определение референтного значения эталона массы в пилотной лаборатории.

1.5.1. Определение условной массы эталона.

Допустим, что полученные результаты калибровки принадлежат нормальному распределению. Используя доверительный интервал 99%, можно произвести фильтрацию результатов калибровки по следующей формуле:

                                                            (1)

где - среднее арифметическое значение условной массы,

n- количество результатов калибровки (объём выборки),

- среднеквадратическое отклонение выборки,

- значение распределения Стьюдента с числом степеней свободы n-1.

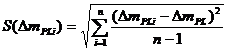                                                                           (2)

Выберем значения условной массы (результаты калибровки), которые находятся в доверительном интервале (рис. 2). Из отфильтрованных результатов калибровки можно определить условную массу (референтное значение), как среднее арифметическое значение:

                                                                                                 (3)

1.5.2. Оценка неопределённости условной массы эталона.

Неопределённость – это компонент результата измерений, характеризующий дисперсию значений, в которой находится истинное значение.

Расширенная неопределённость измерения массы состоит из нескольких компонентов [3]:

·                     Стандартная неопределённость, полученная в процессе взвешивания, рассчитывается по следующей формуле:

                                                                                           (4)

где 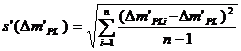 - общее стандартное отклонение.

Примечание: в данном случае стандартная неопределённость была рассчитана из отфильтрованных результатов.

·                     Стандартная неопределённость референтного эталона массы – берётся из калибровочного сертификата, а также учитывается дрейф эталона:

                                                                                      (5)

где U – неопределённость референтного эталона массы из предыдущего калибровочного сертификата, делится на коэффициент охвата k=2, то есть для нормального распределения это 2. Калибровка эталонов в пилотной лаборатории производится один раз в два года. Латвийские национальные эталоны калибруются в основном в Дании (DFM).

 – дрейф референтного эталона массы – это величина, характеризующая изменение массы эталона во времени с момента изготовления.

·                     Неопределённость, связанная с влиянием аэростатических сил, рассчитывается по следующей формуле:

                                                                                       (6)

где , - плотности референтного и тестируемого эталона,

- плотность воздуха.

·                     Неопределённость измерительного прибора .

В данном случае неопределённость компаратора массы  была взята из предыдущего калибровочного сертификата. Калибровка компаратора массы в пилотной лаборатории осуществляется один раз в год.

·                     Комбинированная неопределённость условной массы тестируемого эталона рассчитывается по формуле:

                                                            (7)

·                     Расширенная неопределённость условной массы тестируемого эталона рассчитывается по формуле:

                                                                                            (8)

где k=2 при доверительном интервале 95%, то есть 2.

Таким образом, условная масса и её расширенная неопределённость в пилотной лаборатории были получены для номиналов 100 мг, 1 г, 50 г, 100 г, 500 г, 1 кг и 20 кг.

 

1.6. Анализ данных при сличении результатов пилотной лаборатории с результатами лабораторий-участниц.

Согласно звездообразной маршрутной схеме, эталоны массы были отосланы пилотной лабораторией лабораториям-участницам на калибровку. Далее откалиброванные эталоны были возвращены в пилотную лабораторию вместе с результатами калибровки, полученными в этих лабораториях. Затем было произведено графическое и аналитическое сличение результатов.

1.6.1. Графическая оценка лабораторий-участниц.

В качестве примера можно рассмотреть графическое сличение результатов между лабораториями на номинал 1 кг (рис. 3).

 

Рис. 3. Результаты калибровки лабораторий-участниц на номинал 1 кг.

 

По оси х обозначены лаборатории «PL», «A», «B», «C» и «D». Точки на графике обозначают полученные результаты калибровки условной массы для каждой лаборатории (ось y), а вертикальные линии (ось y) характеризуют полученную расширенную неопределённость условной массы .

На графике можно видеть, что результат лаборатории «А» не совпадает с результатом, полученным в пилотной лаборатории «PL». Это говорит о том, что результат лаборатории «А» является неудовлетворительным на номинал 1 кг. А также заметно, что в лабораториях «C» и «D» получена довольно большая неопределённость.

1.6.2. Аналитическая оценка лабораторий-участниц.

Для того, чтобы подтвердить выводы, сделанные при графическом анализе, необходимо применить аналитический анализ через коэффициент  [4]:

                                                                                       (9)

где  – расширенная неопределённость, полученная в i-той лаборатории для результата ,

 – условная масса, измеренная в пилотной лаборатории,

 – расширенная неопределённость условной массы, полученной в пилотной лаборатории.

·                     если , то результат удовлетворительный,

·                     если , то результат неудовлетворительный.

Для подтверждения выводов, для каждой лаборатории и каждого номинала был рассчитан коэффициент . В качестве примера приведена таблица (таблица 1), в которой отображены значения коэффициента  на номинал 1 кг.

 

Таблица 1.

Значения коэффициента E_n (1 кг).

LABi	PL	A	B	C	D
PL	-	1,64	-0,22	-0,14	0,00
A	-1,64	-	-1,69	-0,77	-0,02
B	0,22	1,69	-	-0,12	0,00
C	0,14	0,77	0,12	-	0,00
D	0,00	0,02	0,00	0,00	-

 

Действительно, у лаборатории «А» по отношению к пилотной лаборатории значение коэффициента  превысило единицу. Значит, результат в лаборатории «А» на номинал 1 кг является неудовлетворительным.

Таким образом, было произведено аналитическое и графическое сличение результатов для остальных номиналов.

На этом этапе исследований можно было бы остановиться, но рассчитанный коэффициент  показал, что неудовлетворительный результат получен только в лаборатории «А». В то же время, графический анализ показывал, что имеется проблема в лабораториях «C» и «D». Основной проблемой этих лабораторий была большая неопределённость, которую хорошо можно было видеть на графике.

 

1.7. Исследование неопределённости и наилучшей способности измерения в лабораториях-участницах.

Полученную расширенную неопределённость в процессе межлабораторного сравнения для каждого участника необходимо было сличить с допустимой неопределённостью, которая согласно международной рекомендации OIML R 111 не должна превышать одной трети от допустимой погрешности номинала на тот класс точности, на который аккредитована лаборатория. Иными словами, должно соблюдаться неравенство:

                                                                                                (10)

Сличение фактической и допустимой неопределённости приведено в таблице 2.

 

Таблица 2.

Фактическая и допустимая неопределенность.

Номиналы	A (класс М1)		B (класс F1)		C (класс F1)		D (класс F1)
	Факт. мг	Доп. мг	Факт. мг	Доп. мг	Факт. мг	Доп. мг	Факт. мг	Доп. мг
100 мг	0,032	0,166	0,0017	0,0167	0,142	***	0,026	***
1 г	0,031	0,333	0,004	0,033	0,156	0,033	0,026	0,033
50 г	0,042	1,0	0,021	0,100	0,222	0,100	0,033	0,100
100 г	0,058	1,667	0,016	0,167	0,308	0,167	0,046	0,167
500 г	1,584	8,33	0,081	0,833	4,591	0,833	0,120	0,833
1 кг	2,103	16,67	0,160	1,667	4,977	1,667	230	***
20 кг	118,39	333	13,67	33,3	58,50	33,3	230	***

 

Фактические значения, превышающие допустимые, обозначены жирным шрифтом.

Далее было произведено сличение полученной в ходе межлабораторного сравнения расширенной неопределённости и наилучшей способности измерения (НСИ), взятой из аккредитационного сертификата (таблица 3).

 

Таблица 3.

Фактическая неопределенность и НСИ.

Номиналы	A (класс М1)		B (класс F1)		C (класс F1)		D (класс F1)
	Факт. мг	НСИ мг	Факт. мг	НСИ мг	Факт. мг	НСИ мг	Факт. мг	НСИ мг
100 мг	0,032	0,17	0,0017	0,016	0,142	***	0,026	***
1 г	0,031	0,21	0,004	0,033	0,156	0,14	0,026	0,025
50 г	0,042	0,25	0,021	0,10	0,222	0,20	0,033	0,029
100 г	0,058	0,25	0,016	0,16	0,308	0,26	0,046	0,036
500 г	1,584	1,3	0,081	0,83	4,591	4,2	0,120	0,011
1 кг	2,103	1,7	0,160	1,6	4,977	4,6	230	***
20 кг	118,39	91	13,67	100	58,50	41,1	230	***

 

Из таблицы 3 можно видеть, что у лабораторий имеется проблема с пониманием наилучшей способности измерения.

Также было произведено сличение между НСИ и допустимой неопределённостью (Таблица 4).

 

Таблица 4

НСИ и допустимая неопределенность.

Номиналы	A (класс М1)		B (класс F1)		C (класс F1)		D (класс F1)
	НСИ мг	Доп. мг	НСИ мг	Доп. мг	НСИ мг	Доп. мг	НСИ мг	Доп. мг
100 мг	0,17	0,166	0,016	0,0167	***	***	***	***
1 г	0,21	0,333	0,033	0,033	0,14	0,033	0,025	0,033
50 г	0,25	1,0	0,10	0,100	0,20	0,100	0,029	0,100
100 г	0,25	1,667	0,16	0,167	0,26	0,167	0,036	0,167
500 г	1,3	8,33	0,83	0,833	4,2	0,833	0,011	0,833
1 кг	1,7	16,67	1,6	1,667	4,6	1,667	***	***
20 кг	91	333	100	33,3	41,1	33,3	***	***

 

Из таблицы 4 видно, что наилучшая способность измерения превышает допустимую неопределённость. Это говорит о том, что аккредитующим органом в аккредитационном сертификате была допущена ошибка.

 

Выводы

 

Результаты лабораторий можно свести в общую таблицу 5.

 

Таблица 5.

Анализ результатов (“+”-удовлетворительный результат, “–” неудовлетворительный результат).

Примечание: знак ***” напротив номиналов показывает, что на эти номиналы лаборатория не аккредитована.

 

Из таблицы 5 видно, что по коэффициенту можно сделать поспешные выводы о результатах сличения между лабораториями. Поэтому в межлабораторном сравнении необходимо использовать графический и аналитический методы сравнения. При проведении межлабораторного сравнения необходимо огромное внимание уделить полученной неопределённости, сравнить её с допустимой, а также сравнить с наилучшей способностью измерения.

 

Литература

 

1.                   Пугачев В. Теория вероятностей и математическая статистика. – Москва: Наука, 2002. – 496 стр.

2.                   Севастьянов Б. Курс теории вероятностей и математической статистики. – Москва: Наука, 1982. – 238 стр.

3.                   International Recommendation OIML R 111. – Paris: International Organization of Legal Metrology, 2004. – 78 p.

4.                   ISO Guide 43-1:1997. Proficiency testing by interlaboratory comparisons. Part 1. Development and operation of proficiency testing schemes. – Geneva: International Organization for Standardization, 1997. – 16 p.

5.                   ISO 17025. General requirements for the competence of testing and calibration laboratories. – Geneva: International Organization for Standardization, 2005. – 37 p.

6.                   ISO 13528. Statistical methods for use in proficiency testing by interlaboratory comparisons. – Geneva: International Organization for Standardization, 2005. – 66 p.

7.                   JCGM 100:2008. Guide to the Expression of Uncertainty in Measurement. – Geneva: International Organization for Standardization, 2008. – 120 p.

8.                   Laaneots R., Mathiesen O. An Introduction to Metrology. – Estonia: The Publishing Office of the Tallinn University of Technology, 2006. – 272 p.

9.                   Nava J., Becerra L.O. Interlaboratory mass comparison between laboratories belonging to SIM – sub-regions coordinated by CENAM. – Mexico: CENAM, 2006. – 8 p.

10.               Report of EUROMET key comparison of multiples and submultiples of the kilogram.-Sweden: EUROMET, 2008. – 14 p.

11.               Report on EUROMET key comparison of 1 kg standards in stainless steel. – UK: National Physical Laboratory, 2008. – 21 p.

12.               Woger W. Remarks on the E_n – criterion Used in Measurement Comparison. – Braunschweig: PTB-Metteilungen, 1999. – 27 p.

 

Поступила в редакцию 15.06.2010 г.