Взрывающиеся решения
нелинейных гиперболических уравнений
Гаджиев Тахир Сади оглу,
доктор физико-математических
наук, профессор Института математики НАНА,
Расулов Рафиг Абдулали оглу,
кандидат
физико-математических наук, доцент Азербайджанского института учителей.
This research article
deals with the behavior nonlinear evulsions solution of the equations in
limited oblast. Such kind of equations describe the explosive solution of the
nonlinear equation of a hyperbolic type
In the conclusion of
the article the author showed that even the simple nonlinear phenomenon
develops the limited time, depending of critical indicators, the solution of
nonlinear hyperbolic equations develop unlimited in limited time.
В работе
рассматриваются неограниченно растущие за конечное время решения нелинейных
гиперболических уравнений.
Особое место
в теории нелинейных уравнений занимают исследования неограниченных решений или
режимов с обострением.
Даже в самых
простых случаях нелинейности, в зависимости от критического показателя, решения
нелинейного гиперболического уравнения могут неограниченно расти за конечное
время, то есть существует 
такое, что
Соответствующие
результаты, также называют теоремами типа Фуджиты и Фуджиты-Хаякавы (см. 
) . Для нелинейных гиперболических уравнений особо отменим в
этом направлении работы 
1.
Рассмотрим уравнение
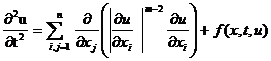(1)
в ограниченной
области 
с негладкой границей. Oбозначим 
. Относительно 
условия уточним позже.
Предположим выполнения краевого условия
(2)
и начальных
условий
(3)
в некоторый
области 
предполагая гладкость
функций 
и 
. Будем изучать условия, при которых обобщенное решение из 
в 
(4)
при
некотором 
При 
и при линейной главной
части имеются множество работ по изучению свойств решений имеющих (4).
Например, 
и др. Мы покажем, что
если 
решение задачи (1)-(3),
где 
и 
«не очень малы», то
имеет место (4). При малых , , если 
, то 
не зависит от 
. Установим достаточные условия на 
при которых любое решение
задачи (1)-(3) при 
, 
, ≢0 , ≢0 имеет «взрыв» без ограничения малости на , ,
Обобщим
решением задачи (1)-(3) в 
назовем функцию
такую, что
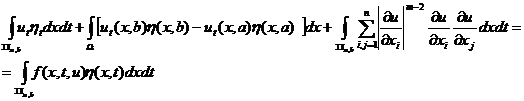(5)
где 
- произвольная функция из 
Пусть 
собственная функция
спектральной задачи для оператора 
соответствующая 
, 
Сформулируем
некоторые вспомогательные предложения из 
. Определим 
- оператор 
Лемма 1. Существует
положительных собственное значение спектральной задачи для оператора 
, которому соответствует положительная в 
собственная функция.
Лемма 2. Пусть 
на 
и
,
для любого 
Тогда 
во всей области .
Предположим,
также выполнение условия
(А)
. условие (А) показывает, что
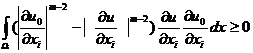
Теорема 1. Пусть 
и при 
, 
, где 
и выполняется условие
(А). Существует 
такая, что если
тогда 
где 
Доказательство. Допустим противное.
Тогда 
решение уравнение (1)
в и выполнено условие
(2) на 
. В силу леммы 2 
в . Подставим в (5) 
где 
в собственная функция спектральной
задачи для оператора 
- соответствующая собственному значению 
. Такое собственное значение и такая собственная функция
существует с силу леммы 1. Получим, что
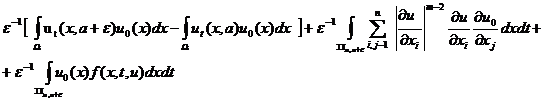(6)
Используя
условие (А) из (6) получим
(7)
Устремив в
(7) 
к нулю, получим, что
почти при всех 
или
(8)
Отсюда обозначив
,
имеем
(9)
В силу неравенства
Гёльдера
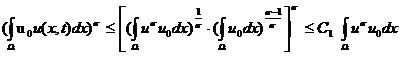
Тогда имеем
, 
(10)
Итак
получено неравенство
, где 
Умножим на 
, тогда
отсюда 
Проинтегрируем
по 
от 0, до . Тогда
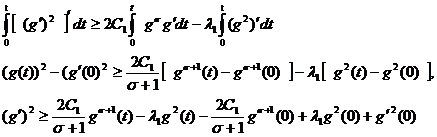
Обозначим 
. Тогда если 
, получим
. Отсюда 
Если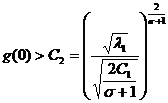 
, то
, что означает 
.
Теорема
доказана.
Для
уравнений, рассмотренных в пункте 1, мы использовали условие (А). Условие (А)
фактически, условие теорем сравнения для нелинейных уравнений. В некоторых случаях
нелинейности можно обойтись без условия (А).
Рассмотрим
следующее уравнение
(11)
в ограниченной
области
Через в ,
обозначим первую собственную функцию задачи 
в , 
на , и через соответствующие
собственное значение .
Теорема 2. Пусть 
и при 
. Существует 
такая, что если 
тогда 
, где
Доказательство. Допустим обратное.
Тогда -решение уравнения
(11) в и выполнено условие
(2) на . В силу леммы 2 в . Подставим в соответствующее интегральное тождество 
; 
где в собственная функция
спектральной задачи для оператора Лапласа, соответствующая собственному
значению . Получим
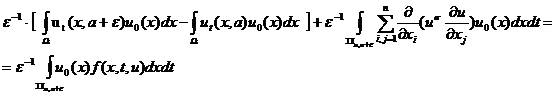(12)
Устремив в
(12) к нулю, получим
(13)
где 
Рассмотрим
первый интеграл справа в (13).
Пуст 
в и 
Обозначим
поверхность вырождения уравнения (11) 
границу носителя решения
через 
. Тогда 
в 
. По формуле Грина имеем
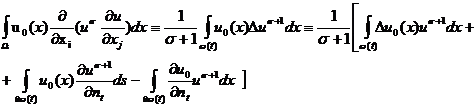(14)
где 
- производное по направлению внешней нормали к . Так как 
на и в силу непрерывности волнового потока 
при 
.
Поэтому два последних
интеграла в (14) равны нулю.
Тогда
получаем
(15)
Используя
(15) и учитывая, что 
в из (13) получим
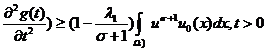(16)
Если 
, так как 
выпуклая функция при , то с помощью неравенства Йенсена получим следующую оценку
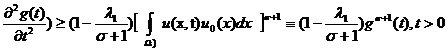(17)
Отсюда следует,
что 
(и значит 
) остаётся ограниченной в течении времени, не большего
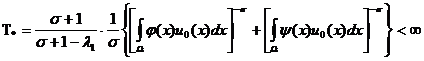т.е. существует 
такое, что при
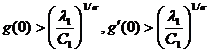
Отметим, что
при 
из (17) вытекает ограничность при всех 
Литература
1.
Y.Ebihаra, Sh.Kawashima, N.Levine. ”On solutivn 
”, // Funccial
Ekvac, 38(1995), № 3, p.539-544.
2.
H.Levine. “Instability and nonexistence of global
solutions to nonlinear wave equations of the from 
” // Trans. Amer. Math. Soc., 1974, 192, p.1-21.
3.
L.Tolksdorf.
“On quasilinear boundary value problems in domains with corners // Nonlinear Anal., 1981, Vol. 5, № 7, p.721-735.
4.
Д.Гилбарг, Н.Трудингер. Эллиптические дифференциальные
уравнения с частными производными второго порядке. М., Наука, 1989.
5.
Fujita
H. On the blowing up of solutions to the Caishy problem for 
// J. Fac. Sci. Univ. Tokyo. I, 1996, v.13, pp.109-124.
6. Hayakawa K. On nonexistence of
global solutions of some semi-linear parabolic differential equations // Proc.
Japan Acad.Ser A. Math. Sci., 1973, v.49, pp.503-505.
Поступила в редакцию 10.03.2010 г.