Об одном соотношении задачи Дарбу для уравнения
Трикоми
Акимов
Андрей Анатольевич,
кандидат физико-математических наук,
доцент кафедры математического анализа,
Галиаскарова
Гузель Рафкатовна,
кандидат
физико-математических наук, доцент кафедры математического анализа.
Стерлитамакская государственная
педагогическая академия им. З. Биишевой.
Рассмотрим уравнение
, (1)
в области 
, ограниченной при 
отрезком
с концами в точках 
и 
, характеристикой 
и кривой 
, выходящей из точки 
и пересекающей
характеристику 
в точке 
.
Будем рассматривать только те
кривые , которые в характеристических координатах задаются
уравнением 
Задача Дарбу. Найти
в области функцию 
, удовлетворяющую условиям:
(2)
, 
(3)
; (4)
; (5)
где 
−заданные достаточно гладкие функции, 
−абсцисса точки .
В области решение уравнения (1),
удовлетворяющее данным Коши 
дается формулой [ 1 ]
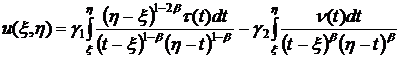(6)
где
, 
, 
.
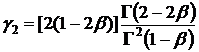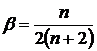В дальнейшем будем считать, что 
. Тогда из (6), если принять во внимание 
и краевое условие (4), получим
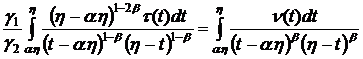. (7)
Покажем, что из равенства (7)
следует следующее соотношение между 
и 
:
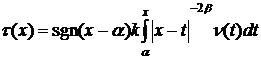, (8)
где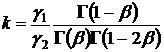 
.
При 
имеем
.
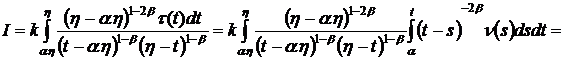
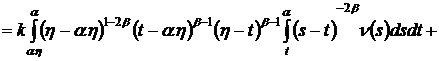
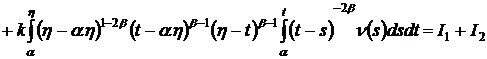Вычислим 
, предварительно изменив порядок интегрирования:
.
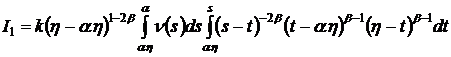Выполним в последнем интеграле
следующую замену 
.
.
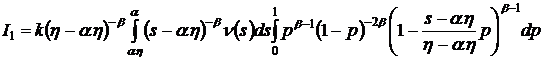Применяя интегральное
представление [ 2 ] гипергеометрической функции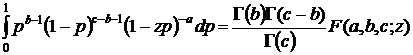 
и учитывая, что 
, окончательно получим
.
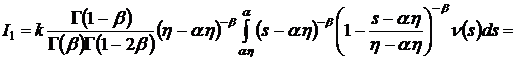
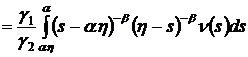Аналогично, поменяв порядок
интегрирования и, сделав замену 
, применяя интегральное представление гипергеометрической
функции и формулу, получим:
.
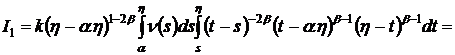
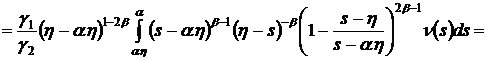
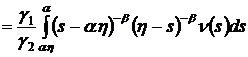Складывая интегралы и убеждаемся, что при
,
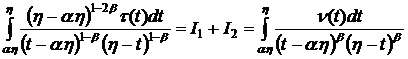если определяется по
формуле (8). Аналогично проверяем справедливость соотношения (8) и для 
.
Литература
1.
Смирнов
М.М. Уравнения смешанного типа. М. Наука, 1970, 304 с.
2.
Самко С.
Г., Килбас А. А., Маричев О. И. Интегралы и производные дробного порядка и некоторые
их приложения. Минск., Наука и техника, 1987, 688 с.
Поступила
в редакцию 16.12.2010 г.