Прогнозируемость фондовых индексов с помощью константы Херста
Пучков Андрей Александрович,
магистр экономики Рижского технического университета.
Целью настоящей статьи является выявление взаимозависимости устойчивости временного ряда и его будущих значений. Объектом исследования стал старейший среди существующих американских рыночных индексов – индекс Доу-Джонса – DJIA (Dow Jones Industrial Average). В ходе эксперимента были использованы данные за период от 1 октября 1928 года до 7 июля 2011 года [[1]]. Данные индекса за указанный период приведены в нижеследующем графике: по линейной и логарифмической шкалам.
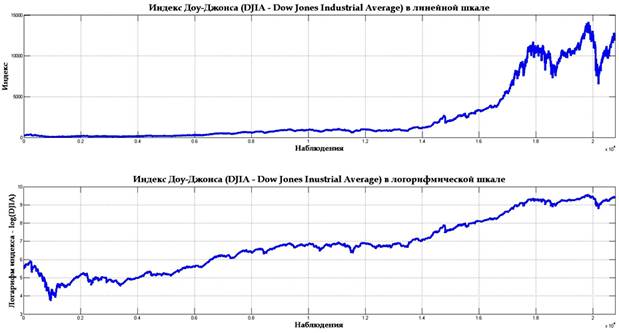
Рис. 1. Индекс Доу-Джонса – DJIA (Dow Jones Industrial Average) за период от 1.10.1928 по 7.07.2011.
Одним из характерных показателей устойчивости или персистентности временного ряда является константа Херста – статистический показатель, выявляющий накопление и наследование прошлой информации временных рядов, т.е. фрактальные свойства ряда. Показатель Херста (H) может принимать значения 0 ≤ H < 1 (от нуля до единицы), причём:
1) значения в пределах 0 ≤ H < 0,5 (от нуля до половины) принято называть розовым шумом и связывать последний с эргодическим или антиперсистентными свойствами;
2) значение равное H=0,5 принято называть белым шумом, оно означает броуновское движение – наблюдения случайны и некоррелированны, следственно настоящие значения временного ряда не влияют на будущие;
3) значения в пределах 0,5 < H < 1 (от половины до единицы) означают наличие фрактальных свойств временного ряда, следственно указывают на персистентные или трендоустойчивые свойства временного ряда [[2]].
Чтобы рассчитать данный индикатор временного ряда, существует множество различных методов – метод, основанный на определении клеточной размерности, метод, основанный на определении стандартного отклонения для разных степеней усреднения, R/S метод, вейлет преобразования и.т.д. Автор данной статьи воспользовался методом Истаса и Ланга, основанном на дискретном преобразовании второй производной [[3]]. Выбор именно этого метода оценки обоснован в разделе результаты эксперимента.
Существует спор в трактовке оценки показателя Херста. Одни считают его показателем, присущем временному ряду на протяжении всего времени, а его изменения объясняются статистической погрешностью. Другие же склонны считать, что рынок может приобретать и терять фрактальные свойства в ходе определённых событий, следственно индикатор Херста имеет смысл только в контексте определённого времени и его изменения могут означать потерю или приобретение временным рядом информационной структуры. Автор данной статьи склоняется к последней гипотезе, но дабы проверить, является ли показатель Херста хорошим показателем трендовидности, производится данное исследование.
Учитывая то, что целью данной статьи является выявление взаимозависимости устойчивости временного ряда с его будущими изменениями на примере индекса Доу-Джонса, логично задаться вопросом – является ли показатель Херста хорошим индикатором трендоустойчивости временного ряда, и если является, то какова взаимосвязь сегодняшнего показателя Херста с будущими приростами индекса на определённых временных горизонтах.
Описание эксперимента
Для реализации поставленной цели, необходимо провести эксперимент – бэк тест, сравнивая исторические значения индикатора Херста с историческими приростами индекса на определённом горизонте прогнозирования. Для реализации эксперимента логично преобразовать индекс по логарифмической шкале (так как показано на нижнем изображении рис. 2).
Необходимо установить, какой период выборки для расчёта показателя Херста оптимален. Слишком длинный период выборки даст скорей оценку персистентности самого ряда, нежели полезную информацию о взаимосвязи показателя с возможными приростами. Слишком короткий период не позволит корректно просчитать показатель Херста по причине отсутствия достаточной накопленной информации рядов или наличия псевдо информационной структуры, которая в процессе перемешивания исчезнет.
Следует определить, какой период (горизонт прогнозирования) обеспечивает наибольшую взаимосвязь между индикатором Херста и будущими приростами, если таковой конечно существует.
В дальнейшем будет описан непосредственно сам эксперимент. Бэк тест (backtesting) осуществляется из каждой точки временной лини, начиная с начала координат и заканчивая последней возможной точкой наблюдения.
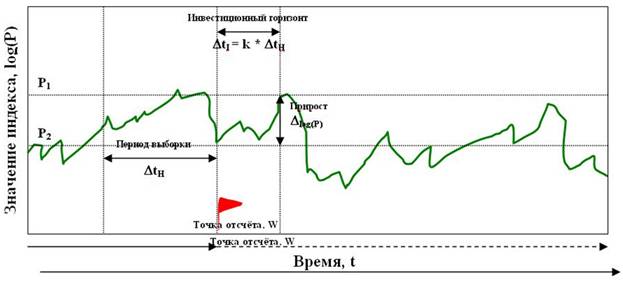
Рис. 2. Иллюстрация эксперимента.
Алгоритм исследования в каждой точки временной оси осуществляется следующим образом:
1) Для расчёта индикатора Херста, отбираются наблюдения P(t), которые находятся слева (в прошлом) от точки отсчёта (W) на длину периода выборки DtH, (причём длина периода выборки подбирается по нарастающей с неким шагом (step), тогда длина периода выборки DtH рассчитывается по формуле:
DtH = i * step, (1)
где: DtH – длина периода выборки; i – индекс глубины выборки (i = 1, …, n); step – шаг выборки; n – максимальное возможное число выборки, учитывая размер данных, точку отсчёта (W) и шаг (step).
В таком случае в выборку P(t) попадут все значения индекса P находящиеся в интервале (W-DtH < t < W). Формула приведена ниже:
P(W-DtH < t < W), (2)
где: P(t) – наблюдения индекса P указанного периода t; W – точка отсчёта; t – параметр времени; DtH – длина периода выборки.
2) По отобранным данным производится расчёт индикатора Херста согласно выбранному методу.
3) Для расчёта прироста на определённом горизонте прогнозирования определяется точка справа от точки отсчёта (W). Эта точка удалена вправо от (W) на длину горизонта прогнозирования (DtI). Логично связать длину горизонта прогнозирования с глубиной периода выборки (DtH), используемого для расчёта индикатора Херста по формуле:
DtI = k * DtH, (3)
где: DtI - длина горизонта прогнозирования; k - коэффициент масштабирования; DtH – длина периода выборки.
Коэффициент масштабирования подбирается таким образом, чтобы связь между индикатором Херста и приростом индекса была наибольшей (подробней об этом на шаге 9).
4) После определения точки справа от точки отсчёта по формуле (4), находится значение индекса P1, соответствующее заданной точке – это P1(W+DtI).
W+DtI, (4)
где: W – точка отсчёта; DtI - длина горизонта прогнозирования.
5) Определяется значение индекса P2, соответствующее точки отсчёта W – это P2(W).
6) Вычисляется прирост индекса Dlog(P) по формуле:
Dlog(P) = (log(P2) – log(P1))/ DtI, (5)
где: P1 - значение индекса P, соответствующее точке P1(W+DtI); P2 - значение индекса P, соответствующее точке отсчёта W - P2(W); W – точка отсчёта; DtI - длина горизонта прогнозирования; log – натуральный логарифм по основанию е; log(P2) – log(P1) – прирост индекса за определённый временной горизонт [[4]].
Для определения связей логично взять прирост индекса по модулю – абсолютный прирост. Данный прирост необходимо поделить на величину горизонта прогнозирования DtI, получая усреднённый логарифмический прирост индекса.
7) Значения индикатора Херста (полученные на втором шаге) и прирост индекса (полученный на шестом шаге) объединяются для дальнейшего изучения. Логично связать полученные значения с точкой отсчёта (W).
8) После сохранения данных следует переместить точку отсчёта на один шаг вправо по временной шкале и провести все действия сначала по шагам 1-7;
9) После получения данных на всём возможном временном интервале следует адоптировать подбираемые параметры: step и k. Значения подбираются эмпирически, но при этом связь между данными (показателем Херста и приростами) должна улучшаться. В качестве меры определяемых видов связи следует использовать коэффициент Пирсона, Кэндала и Спирмана [[5]].
Результаты эксперимента
В ходе эксперимента были установлены следующие факты:
1. Метод расчёта показателя Херста.
В ходе эксперимента были протестированы четыре метода расчёта показателя Херста: метод, основанный на определении клеточной размерности, метод, основанный на определении стандартного отклонения для разных степеней усреднения, R/S метод и метод Истаса и Ланга, основанный на дискретном преобразовании второй производной. В ходе тестирования методов был выбран метод Истаса и Ланга, так как он давал более гладкие и более пригодные для анализа результаты.
2. Период выборки для расчёта показателя Херста.
Оптимальны период выборки, удовлетворяющий условиям, выдвинутым в начале эксперимента, является 100 (сто) торговых дней или 100 (сто) наблюдений. При этом было доказано, что увеличенная выборка скорее уменьшает возможность отследить возможные будущие изменения индекса, нежели несёт в себе большую информацию. При увеличении периода выборки, результаты показателя Херста смещался вправо к результату 0,65, что плохо влияло на взаимосвязь показателей Херста и абсолютных приростов индекса.
В любом случае не доказано, что увеличивая размер выборки, улучшается прогнозируемость будущих изменений индекса. При уменьшении количества выборки возникали некорректно посчитанные значения показателя Херста, выходящие за рамки границ показателя (0 ≤ H < 1).
3. Период горизонта прогнозирования.
В ходе подбора коэффициента масштабирования k, а следственно и горизонта прогнозирования, было установлено, что увеличение временного горизонта никак не улучшает корреляцию между константой Херста и приростами индекса. Увеличение горизонта как бы «размывает» абсолютные приросты индекса, ввиду чего уменьшается связь между величинами. Однако в ходе эксперимента было установлено, что коэффициента масштабирования k = 0,15 даёт немного лучшие результаты по коэффициенту корреляции Пирсона, Кэндала и Спирмана, нежели другие значения. Следственно горизонт прогнозирования составляет 15 торговых дней.
4. Взаимозависимость константы Херста и приростов индекса.
Эксперимент по выявлению взаимозависимости показал, что взаимозависимость между величинами действительно существует. Однако последняя едва ли может быть объяснена линейными показателями корреляции. Результаты отображены ниже.
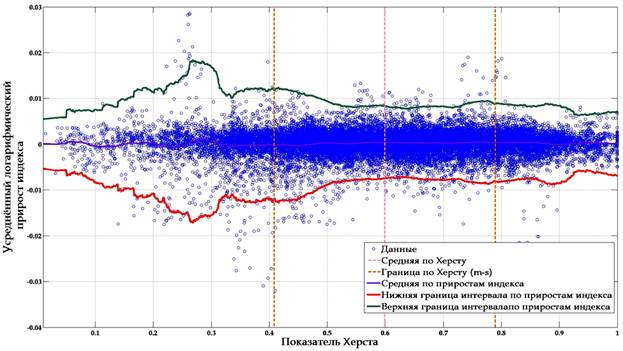
Рис. 3. Взаимозависимость константы Херста и приростов индекса Доу-Джонса – DJIA (Dow Jones Industrial Average).
На рис. 3 отображены данные по эксперименту: по оси Х – показатель Херста, по оси Y – усреднённый логарифмический прирост индекса. На первый взгляд кажется, что данные взаимонезависимы, однако при детальном рассмотрении, очевидно, что данные в интервале 0,1 ≤ H < 0,5 (от нуля до половины), содержат большее стандартное отклонение, следственно и более широкие границы доверительного интервала. Интервал 0,5 < H < 0,9 представляется менее рискованным, так как стандартное отклонение приростов индекса в данном интервале наименьшее. Интервалы H < 0,1 и 0,9 < H не представляются анализируемыми по причины недостаточности данных.
Что касается самого индекса Доу-Джонс, можно заметить, что индекс демонстрирует трендоустойчивость и довольно большое количество данных попадает в интервал от 0,4 < H < 0,8 ( с центром H = 0,6), причём большая часть интервала 0,5 < H < 0,8 является менее рискованной с точки зрения описательной статистики. Предположительно именно трендоустойчивотью индекса объясняется его предпочтительность среди инвесторов.
Однако прежде чем сделать выводы о трендоустойчивости индекса, а также о связи между показателем Херста и трендоустойчивостью, следует рассмотреть рис. 3.
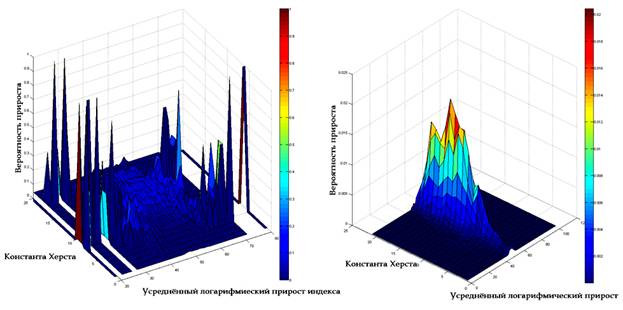
Рис. 4. Взаимозависимость константы Херста и приростов индекса Доу-Джонса – DJIA (Dow Jones Industrial Average) – гистограмма 3D.
Левое изображение на рис. 4 показывает, как распределена вероятность прироста индекса при определённом показателе Херста, в свою очередь правое изображение данного рисунка показывает, как распределена вероятность прироста индекса при различных показателях Херста, учитывая распределения вероятности самого показателя Херста. Для данных 3D гистограмм были взяты следующие границы интервалов: для показателя Херста от 0 до 1 с интервалом 0,05; для величины приростов от -5% до +5% с интервалом 0,1%.
При детальном анализе графиков видно, что наиболее часто показатель Херста встречается в интервале близком к центру (0,4 < H < 0,8), в остальных же интервалах данный показатель встречается гораздо реже и именно в этих интервалах встречаются приросты индекса, существенно отклоняющиеся от центральных значений. Такое поведение, скорее всего, связано с наличием толстых хвостов в распределении вероятности приростов индексов, нежели с показателем Херста. Данный фактор, во-первых, усложняет моделирование приростов индекса в упомянутых интервалах, во-вторых, даёт понять, что невозможно выбрать наиболее лучший интервал показателя Херста, в котором приросты индекса с большой вероятностью будут лежать в определённом доверительном интервале.
Любопытно при всём том заметить, что показатель Херста фактически никак не связан с центром распределения приростов индекса: было бы несправедливо считать, что индикатор Херста позволяет отследить периоды, когда рост индекса наиболее вероятен. Скорее наоборот – центральное значение приростов индексов существенно не отклоняется от нулевого значения и лежит параллельно оси показателя Херста (см. рис. 3).
Выводы
Исходя из результатов эксперимента можно сделать следующие выводы:
1. Взаимозависимость константы Херста и приростов индекса.
Отвечая на изначальный вопрос, существует ли связь между константой Херста сегодня и будущими значениями индекса, следует ответить – да, существует, но не линейная, а скорее стохастическая. При выявлении зависимости на примере конкретного индекса было доказано, что при показателе Херста в интервале 0,1 ≤ H < 0,5, стандартное отклонение будущих приростов индекса существенно возрастает. Это означает, что рассчитывая константу Херста для индекса сегодня, при попадании результата в указанный интервал, логично предположить, что вероятность отклонения индекса становится выше. Однако невозможно сделать предположение о направлении (знаке) данного прироста. В случае же попадания рассчитанного показателя в интервал 0,5 < H < 0,9, можно предположить, что вероятность большого прироста индекса существенно меньше. Но при всём том невозможно выбрать «лучший» показатель константы Херста в данном интервале, так как нельзя утверждать, что, например, показатель Херста 0,6 более рискованный, нежели 0,8. Во всяком случае, это не следует из результатов эксперимента.
Также невозможно отдать предпочтение определённой константе Херста и по причине «толстых хвостов» распределения приростов индекса. Данное обстоятельство указывает на трудность моделирования приростов в заданном интервале константы Херста, особенно если этот интервал представлен реальными данными не густо. Также данное обстоятельство указывает на то, что константа Херста никак не решает проблему «толстых хвостов» - то есть при моделировании приростов индекса придётся считаться с необходимостью отразить в моделях «выбросы».
2. Длина горизонта прогнозирования.
Если предположить, что возможно прогнозировать будущие приросты индекса, логично определить максимальный горизонт прогнозирования. Учитывая результаты эксперимента, следует признать, что возможно прогнозировать поведение индекса на ближайшие дни – ориентировочно до 15 торговых дней. Не было доказано, что прогнозирование на более длинные горизонты давали бы лучшие результаты, но не было доказано и то, что прогнозирование на более короткие горизонты существенно обеспечило бы лучшие результаты. Однако надо понимать, что эти результаты трудно применить к другим индексам или временным рядам.
3. Практическое применение.
Естественным заключением статьи является практическая сторона – применение выводов исследования. Исходя из вывода о невозможности предсказания направления (знака) прироста индекса на основе показателя Херста, следует заключение, о том, что константу Херста можно использовать только как меру риска, например при сдерживании риска выбирать показатель Херста в интервале 0,5 < H < 0,9 и/или наоборот – при усилении риска выбирать показатель Херста в интервале 0,1 < H < 0,5.
Литература
1. Стрыгин Александр Юрьевич. Анализ фрактальных свойств финансово-экономических процессов в экономике РФ. - Санкт-Петербург, Государственный университет, Высшая школа экономики. 2004. год, 104 стр.
2. Istas, J.; G. Lang (1994), «Quadratic variations and estimation of the local Holder index of a Gaussian process» Ann. Inst. Poincare, 33, pp.
3. forexautomaton.com. Logarithmic returns. [http://forexautomaton.com/research/37-keyconcepts/49-logarithmicreturns] (Accessed 11 July. 2011.).
4. http://www.yahoo.com. Dow Jones Industrial Average. Historical Prices. [http://finance.yahoo.com/q/hp?s=%5EDJI+Historical+Prices] (Accessed 8 July. 2011.).
5. www.statsdirect.com. Spearman's rank correlation. [http://www.statsdirect.com/help/nonparametric_methods/spear.htm] (Accessed 11 July. 2011.).
Поступила в редакцию 12.07.2011 г.
[1] http://www.yahoo.com. Dow Jones Industrial Average. Historical Prices. [http://finance.yahoo.com/q/hp?s=%5EDJI+Historical+Prices] (Accessed 8 July. 2011.).
[2] Стрыгин Александр Юрьевич. Анализ фрактальных свойств финансово-экономических процессов в экономике РФ. - Санкт-Петербург, Государственный университет, Высшая школа экономики. 2004. год, 104 стр. – 64, стр.
[3] Istas, J.; G. Lang (1994), «Quadratic variations and estimation of the local Holder index of a Gaussian process» Ann. Inst. Poincare, 33, pp. 407-436.
[4] forexautomaton.com. Logarithmic returns. [http://forexautomaton.com/research/37-keyconcepts/49-logarithmicreturns] (Accessed 11 July. 2011.).
[5] www.statsdirect.com. Spearman's rank correlation. [http://www.statsdirect.com/help/nonparametric_methods/spear.htm] (Accessed 11 July. 2011.).