Расчетная схема разделения сыпучего материала на вибрирующей сетке

Рудакова Елена Вячеславовна,

аспирант Белгородского государственного технологического университета им. Шухова,

преподаватель кафедры информационных систем и естественнонаучных дисциплин Курского института социального образования (филиал) РГСУ.

Научный руководитель – доктор технических наук, профессор, зав. кафедрой «Материалы и оборудование» Белгородского государственного технологического университета им. Шухова

Богданов В.С.

Поведение сыпучих сред, таких как, например, песок, гравий или каменный уголь, очень разнообразно и зависит от размера частиц, граничных условий, объемной концентрации, сил действующих на частицы. Вообще сыпучий материал можно рассматривать как некоторую двухфазную среду, состоящую из твердых частиц и газа [1-4].

В данной статье рассматривается сыпучий материал как некоторая совокупность твердых частиц различного размера. Модель разделения сыпучего материала на вибрирующей сетке построена с использованием результатов приведенных в работах [2].

Частицы малого диаметра могут проникать через сетку, а частицы большого диаметра остаются на поверхности сетки.

Точный расчет для каждой частицы напряжений и деформаций, которые вызывает контактное взаимодействие, на современном развитии вычислительной техники не возможен. Поэтому в модели среды моделируется движение только некоторых частиц, выполняющих роль маркеров, по перемещению которых с известной степенью точности можно судить о поведении сыпучего материала в целом. В тоже время, адекватность описания движения сыпучего материала с помощью дискретной модели напрямую зависит от количества частиц, представленных в модели и правильности моделирования процессов взаимодействия между частицами.

Далее рассматривается модель неразрушающего взаимодействия частиц. Природа возникновения сил, действующих на частицы при контакте связана с упругим взаимодействием, диссипацией энергии, сухим трением.

На рис. 1 приведена расчетная схема технологического процесса разделения сыпучего материала по фракциям. На схеме приняты следующие обозначения: 1 - частицы; 2 - разделительная сетка; 3 - корпус грохота.

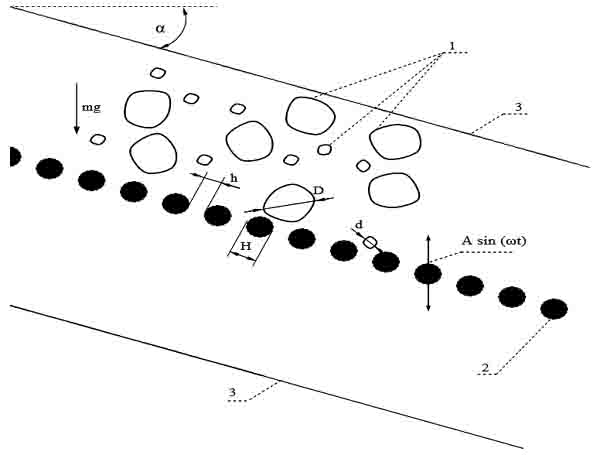
Рис. 1. Расчетная схема системы: 1 – частицы сыпучего материала, 2 –разделительная сетка, 3 – корпус грохота.

На схеме приняты следующие обозначения:

α – угол наклона сетки сепаратора;

H – диаметр сетки сепаратора;

h – минимальное расстояние между проволокой сетки сепаратора;

A- амплитуда колебаний сетки сепаратора;

ω – частота колебаний сепаратора;

d – максимальный диаметр малых частиц;

D – минимальный диаметр больших частиц среды.

Рассмотрим контакт двух сферических частиц i и j, с радиусами R_i и R_j, массами m_i и m_j, моментами инерции I_i и I_j, координатами центров масс (x_i,y_i), (x_j,y_j) , линейными скоростями V_i,и V_j, и угловыми скоростями ω_i,и ω_j соответственно. При столкновении частицы соприкасаются в одной точке - точке контакта С, как показано на рис. 2, где Р – контактная плоскость, касательная к i и j в точке C.

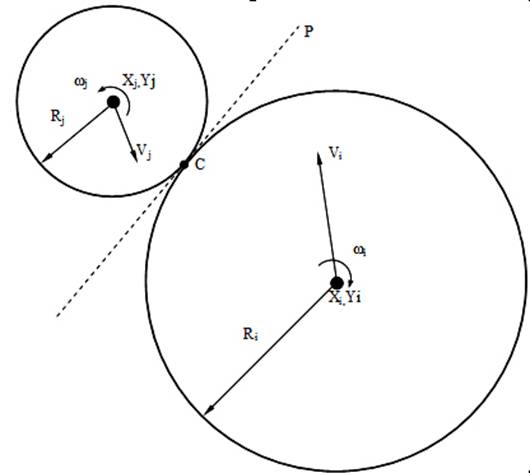
Рис. 2. Контакт двух сферических частиц (начало взаимодействия).

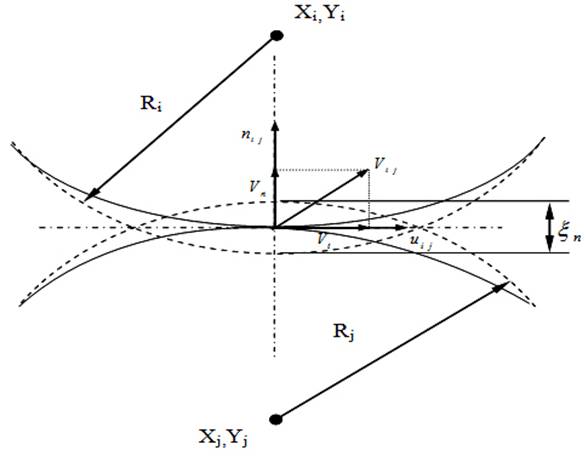
Рис. 3. Контакт двух сферических частиц (деформация поверхности).

В ходе контакта частицы сжимаются, их центры сближаются, а поверхности вблизи точки С деформируются, в результате чего образуется пятно контакта, размер которого мал по сравнению с размерами частиц.

На рис. 3 сплошной линией показаны поверхности деформированных частиц, а пунктиром – поверхности, какими они были бы при отсутствии деформации.

Результирующая сила F_ij передаваемая через пятно контакта от одной частицы на другую, состоит из нормальной компоненты F_n , действующей вдоль общей нормали в точке C, и тангенциальной компоненты F_t , действующей в плоскости контакта P. Тангенциальные компоненты не влияют на нормальные компоненты движения, если упругие свойства материалов двух тел одинаковы.

Даже для разных материалов это влияние мало и им можно пренебречь. Таким образом, можно записать, что

                                                                                                  (1)

                                                                                                   (2)

Где - относительное нормальное смещение частиц,(сжатие в нормальном направлении),  - нормальная компонента относительной скорости,  - относительное тангенциальное смещение частиц (упругое тангенциальное смещение точки контакта),  - тангенциальная компонента относительной скорости.

Тангенциальная сила целиком обусловлена силами трения, поэтому для случая отсутствия трения между поверхностями частиц касательные и вращательные движения нечувствительны к контакту. При наличии трения тангенциальная сила приводит к появлению момента вращения, действующего относительно центров масс частиц и изменяющего их угловые скорости.

Кроме того, поскольку пятно контакта имеет конечные размеры, становиться возможной передача дополнительно к силам еще и результирующего момента. Две составляющие этого момента, действующие в плоскости контакта, называются моментами качения и предопределяют сопротивление движению относительного перекатывания контактирующих тел, называемого трением качения, величина которого в большинстве практических задач мала, для того, чтобы им пренебречь.

Третья компонента результирующего момента действует относительно общей нормали и называется моментом верчения. Момент верчения не учитывается в большинстве моделей сыпучих сред , вследствие минимального влияния на массовое поведение сыпучей среды при значительной вычислительной стоимости процедуры его расчета.

Далее рассмотрим вычисление параметров контакта, необходимых для расчета нормальной и тангенциальной компоненты силы взаимодействия.

Нормальное сжатие частиц будем определять как перекрытие их недеформированных поверхностей .

                                                                                     (3)

Мы будем рассматривать задачу передачу усилия от частицы j на частицу i то есть действие силы F_ij будет направлено от j на i. Поскольку

,

соблюдение порядка следования частиц необходимо для обеспечения правильной ориентации различных векторов.

Определим нормаль контакта n_ij как единичных вектор, ортогональный плоскости Р,

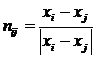                                                                                                         (4)

Тогда относительная скорость частицы j относительно i в точке контакта будет равна:

                                                               (5)

Нормальная компонента относительной скорости запишется в виде:

                                                                                                           (6)

При этом V_n >0 при сближении частиц (стадия нагружения).

Таким образом, нормальный контакт двух упругих частиц может быть представлен как взаимодействие посредством параллельно соединенных элементов упругости и вязкости. Модель тангенциального контакта строиться аналогично, но с добавлением элемента скольжения.

Литература

1.                  Численное исследование актуальных проблем машиностроения и механики сплошных и сыпучих сред методом крупных частиц / Под ред. Ю.М.Давыдова. – М.: Национальная Академия прикладных наук, Международная ассоциация разработчиков и пользователей метода крупных частиц, 1995 . – Т.2. - С. 573.

2.                  Урьев, Н.Б. Физико-химические основы технологии дисперсных систем и материалов /Н.Б.Урьев. – М.: Химия, 1988. – 256 с.

3.                  Jatsun Sergey, Safarov Jamil. Mathematical model of granular material in a vibrating boiling layers. EUROMECH Colloquium 425. 2001. Aberdeen. Scotland.

4.                  Jatsun S., Safarov J. Vibrating engine for robots. Proceedings. CLAWAR 2000. Madrid.P.1016-1021.

Поступила в редакцию 04.02.2011 г.