Силы инерции и их применение

 

Берников Василий Русланович,

инженер.

 

§1. Контур циркулирующей среды. Центробежные силы инерции.

 

Рассмотрим циркуляцию среды по тору (Рис. 1) со средним радиусом R, двигающейся равномерно с угловой скоростью ω относительно центра О. Модуль центробежной силы [1, 281], действующий на точечный элемент потока массой ∆m будет равен ∆F = ∆m ω² R. В любом сечении кольца для одинаковых элементов центробежная сила будет по величине одинакова и направлена по радиусу от центра, растягивая кольцо. От направления вращения центробежная сила не зависит.

 

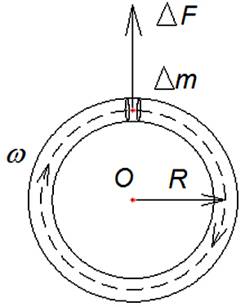
Рис. 1.

 

Теперь произведём расчёт суммарной центробежной силы, действующей перпендикулярно диаметру верхней полуокружности (Рис.2). Очевидно, что в направлении из середины диаметра сила будет максимальна, плавно спадая к краям полуокружности, из-за симметричности кривой относительно средней линии. Кроме того, равнодействующая центробежных сил, действующих параллельно диаметру, будет равна нулю, так как они равны и противоположно направлены.

 

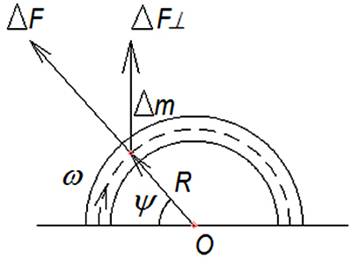
Рис. 2.

 

Запишем элементарную функцию центробежной силы, действующей на точечный отрезок массой ∆m и длиной ∆ℓ:

∆F = ∆m ω² R.                                                                                                         (1)

Масса точечного элемента равна плотности потока, умноженной на его объём

∆m = ρ ∆V,                                                                                                              (2)

длина половины тора по средней линии

ℓ = π R,

где π – число пи.

Объём половины тора

V = π² Rr² = πR π r² = ℓ π r² ,

где r - радиус трубки тора.

Для элементарного объёма запишем

∆V = ∆ℓ π r² .

Известно, что для окружности

∆ℓ = R∆Ψ,

тогда

∆V = π r² R∆Ψ.                                                                                                        (3)

Подставим выражение (3) в (2) получим:

∆m = ρ π r² R∆Ψ.                                                                                                     (4)

Теперь подставим (4) в (1), тогда

∆F = ρ π r² ω² R²∆Ψ.

Центробежная сила, действующая в перпендикулярном направлении (рис.2)

∆F_┴ = ∆Fcos((π/2)- Ψ).

Известно, что cos((π/2)- Ψ) = sin Ψ, тогда

∆F_┴ = ∆F sin Ψ.

Подставим значение для ∆F получим

∆F_┴ = ρ π r² ω² R² sin Ψ ∆Ψ.

Масса половины тора равна

m = ρ π² r² R,

Тогда

∆F_┴ = (m / π ) ω²R sin Ψ ∆Ψ.

Найдём суммарную центробежную силу, действующую в перпендикулярном направлении в интервале от 0 до π

        π

F_┴ = ∫ (m / π ) ω²R sin ΨdΨ.

        0

Проинтегрируем это выражение, тогда получим

                                        π

F_┴ = - (m / π ) ω²R cosΨ│ .

                                                      0

Производим несложные вычисления и в результате получаем суммарную центробежную силу, действующую в перпендикулярном направлении для контура циркулирующей среды

F_┴ = 2m ω² R / π.                                                                                                      (5)

Таким образом, был выделен контур циркулирующей среды, из которых можно составить замкнутую цепь и просуммировать их центробежные силы.

Составим замкнутую цепь из четырёх контуров разных сечений (Рис.3): два контура радиусом R. сечением S и два контура радиусом R1 сечением S1. Причём

S < S1. Пусть радиус R1 < R. Линейная скорость

V = ω R,                                                                                                                   (6)

V1 = Ω R1.                                                                                                              (7)

Плотность циркулирующей среды одинакова. Тогда согласно уравнению неразрывности [3, 333] получим

V/V1 = S1/S = r₁² /r² ,                                                                                               (8)

где r₁ и r радиусы потока циркулирующей среды соответствующего сечения.

Найдём угловую скорость среды нижнего контура, используя уравнения (6),(7),(8)

Ω = ω R r² / r₁² R1.                                                                                                   (9)

Масса контура циркулирующей среды m = ρ π r² ℓ , где ℓ = πR. Аналогично и для нижнего контура массой m₁. Таким образом, можно составить отношение

m₁/ m = r₁² R1/ r R, отсюда

m₁ = m r₁² R1/ r R.                                                                                                    (10)

Теперь, согласно уравнению (5), вычислим центробежную силу для нижнего контура, учитывая уравнения (9), (10) и, производя несложные вычисления получим:

F_┴1 = 2m₁ Ω ² R1 / π = (2m ω² R/ π) (r² / r₁² ).                                                          (11)

При сравнении выражения для центробежной силы верхнего контура (5) и нижнего контура (11) вытекает, что они отличаются на величину (r² / r₁² ).

То есть при r < r₁ центробежная сила верхнего контура больше, чем нижнего.

 

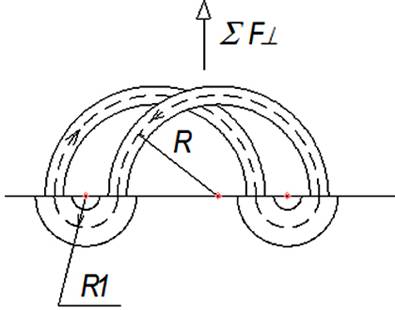
Рис. 3.

 

Равнодействующая центробежных сил, действующая на два контура в верхней полуплоскости (граница верхней и нижней полуплоскости показана тонкой линией) будет равна

F_┴ = 4m ω² R / π.                                                                                                      (10)

Равнодействующая центробежных сил, действующая на два контура в нижней полуплоскости будет противоположно направлена и равна

F_┴1 = 4m Ω² R1 / π = F_┴ r² / r₁².

Очевидно, что суммарная ∑F_┴ центробежная сила, действующая в верхней полуплоскости на два контура, будет действовать в направлении, как показано на рисунке 3. Известно, что центробежная сила – это сила инерции, которая является внешней [2, 379] для замкнутой системы. По второму закону Ньютона производная общего импульса системы тел равна сумме внешних сил [1, 375], действующих на систему, то есть в общем случае можно записать

dK/dt = ∑F_┴.= (4m ω² R / π) (1- (r² / r₁² ).                                                                (11)

Приведём формулу (11) к удобному для технических расчётов виду, для этого выразим массу половины тора через плотность потока циркулирующей среды и объём, а угловую скорость через линейную

∑F_┴.= (4 ρ π r²V²) (1- (r² / r₁² ).                                                                                (12)

Как видим, суммарная центробежная сила зависит от плотности потока, сечений противоположных контуров и линейной скорости потока. От радиуса контуров суммарная центробежная сила не зависит.

Пусть r = 0,025м; r₁ = 0,05м; ρ = 1000 кг/м³; V = 5м/с, тогда ∑F_┴.≈ 147Н.

Таким образом, был выделен базисный контур циркулирующей среды, показана возможность использования контуров циркулирующей среды разных сечений для суммирования центробежной силы в определённом направлении, и изменения общего импульса замкнутой системы тел под действием внешних сил инерции, вызванных внутренними силами.

 

§2. Вращательные системы. Поступательные и центробежные силы инерции.

 

Рассмотрим пару противоположных стержней с грузами на концах, вращающихся вокруг собственного центра масс и вокруг общего центра О с угловой скоростью ω (Рис. 4): один оборот стержня за один оборот вокруг общей оси. Расставим силы, действующие параллельно оси Х, проходящей через общий центр О и положение стержней под углом a = 45 градусов, в плоскости оси Х и общей оси вращения, как показано на рисунке 4. При равномерном принудительном вращении стержней проекция скорости грузов на ось Х не является постоянной и имеет ускорение, то есть параллельно центробежной силе Fц будет действовать одинаковая сила инерции Fин каждого груза. Следует отметить, что стержни участвуют в двух вращательных движениях (собственное и вокруг общей оси), поэтому сложение сил можно производить в системе отсчёта сначала, связанной со стержнем, а потом с общим центром. Простое сложение всех сил можно производить только при поступательном движении элементов системы [4,54]. При сложении сил будем учитывать их направление, расставляя соответственно знаки. Силы инерции являются внешними [4,359] для данной неинерциальной системы и, при их сложении, наглядно видно, что сила инерции нижнего груза левого стержня увеличивается

(Fц2+Fин),

а верхнего уменьшается

(Fц1-Fин).

Для правого стержня модуль сил инерции нижнего груза увеличивается

-(Fц4+Fин),

а верхнего уменьшается

-(Fц3-Fин).

Найдём внешнюю силу, которая создаёт вращающий момент (учитывая, что центробежная сила дальнего груза всегда больше, чем ближнего относительно общей оси), равная разности сил инерции между нижним грузом и верхним левого стержня

(Fц2 - Fц1+ 2Fин),

а правого между верхним грузом и нижним

(Fц4 - Fц3+2Fин).

Так как точки приложения сил симметричны, то можно найти равнодействующую этих сил при простом сложении и, учитывая, что модуль

Fц1 = Fц4 и Fц2 = Fц3

получим следующий результат:

(Fц2 - Fц1+ 2Fин) + (Fц4 - Fц3+2Fин) = 4Fин.

Как видно величина 4Fин положительна, а, следовательно, направлена по оси Х и сила инерции, создаваемая левым стержнем у нижнего груза больше, чем у правого стержня у верхнего груза. И так повторяется за каждый полупериод.

 

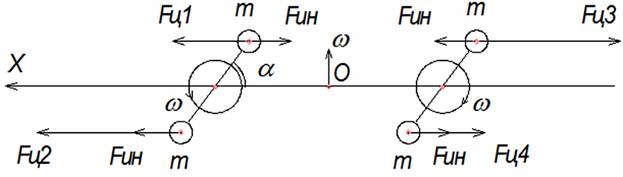
Рис. 4.

 

В общем случае в других сечениях параллельных оси Х и общей оси вращения за полупериод, из-за поворота стержней относительно общей оси, надо рассматривать проекцию 4Fин параллельной оси Х в этом сечении. Угол α за полупериод вращения стержней относительно общей оси меняется от 0 градусов до 90 градусов, а угол между Fин и начальным горизонтальным положением стержня меняется от 0 градусов до 180 градусов. Тогда, в общем случае за каждый полупериод, сумма сил инерции для двух противоположных стержней примет вид:

4Fин ∙ sin2α = 8Fин ∙ cos α ∙ sin α.                                                                         (13)

Выражение 8Fин ∙ sin α ∙ cos α является положительной величиной сил инерции и направлено по оси Х, очевидно не зависящее от направления вращения относительно общей оси. Но два противоположных стержня вызовут только вращательное движение, поэтому вводим другую пару стержней, вращающуюся в другую сторону (рис.5) относительно собственной оси в той же плоскости.

 

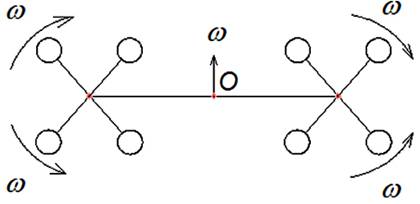
Рис. 5.

 

Другая пара стержней, вращающаяся в обратную сторону, создаст такую же сумму (8Fин∙sin α ∙cos α) сил инерции, расположенную противоположно предыдущей симметрично относительно оси Х и направленную в ту же сторону по оси Х. То есть два левых стержня создадут силу инерции больше, чем два правых. Очевидно, что две внешние одинаковые параллельные силы, приложенные симметрично в одной плоскости с центром масс и направленные в одну сторону, вызовут поступательное движение. Кроме того, эта пара стержней (вращающаяся в обратную сторону) компенсирует вращающие моменты перпендикулярные оси Х. Таким образом поступательные силы инерции принудительного вращения увеличивают общую силу инерции левого стержня, складываясь с центробежной и уменьшают у правого, вычитаясь.

Проведём расчёт модуля силы инерции Fин при принудительном вращении верхнего груза (рис. 4) левого стержня, для этого применим теорему параллелограмма скоростей, то есть разложим линейную скорость V груза на две составляющие параллельную V_II и перпендикулярную V_┴ оси Х (Рис.6). Для нашего случая необходима только V_II = V∙ cos (π/2 – α ). Угол α связан с частотой ω и временем t соотношением

α = ωt/2,                                                                                                                   (14)

так как один оборот стержня происходит за один оборот вокруг общей оси. Тогда

V_II = V∙ cos (π/2 – ωt/2). Линейная скорость V = ωℓ/2, где ℓ/2 радиус окружности или половина длины стержня.

 

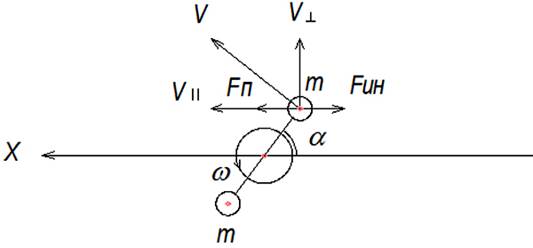
Рис. 6.

 

Тогда V_II = (ωℓ/2)∙ cos (π/2 – ωt/2) = (ωℓ/2) ∙ sin(ωt/2). Продифференцируем параллельную скорость по времени, получим ускорение ε груза по оси Х:

ε = (ω² ℓ/4) ∙ cos(ωt/2).

По второму закону Ньютона сила Fп равна массе груза, умноженной на ускорение

Fп = m(ω² ℓ/4) ∙ cos(ωt/2).

По третьему закону Ньютона силе Fп будет противодействовать такая же сила, но направленная в другую сторону. Это будет поступательная сила инерции Fин. Итак, модуль силы инерции (мгновенное значение) одного груза при принудительном вращении за полупериод будет равен

Fин = m(ω² ℓ/4) ∙ cos(ωt/2).

Учитывая (12) и (13) получим за полупериод

Fин = m(ω² ℓ/4) ∙ cos α ∙ sin 2α.                                                                              (15)

Аналогично проводится расчёт для любого груза относительно угла α с тем же результатом. Теперь подставим выражение (15) в (13), получим суммарную силу инерции F (мгновенное значение) для двух противоположных стержней

F = 4mω² ℓ ∙ cos³(ωt/2) ∙ sin²(ωt/2).                                                                         (16)

Для двух пар противоположных стержней (рис.5), вращающихся в противоположные стороны, надо правую часть выражения (16) умножить на 2. Если добавить ещё две пары противоположных стержней перпендикулярно первым, то можно считать (без вычисления среднего значения функций), что за полупериод будет действовать средняя сила очевидно равная значению для угла α = 45 градусов. Для устранения гироскопического эффекта добавляем ещё такую же ячейку с восемью стержнями, но вращающимися относительно общего центра в противоположную сторону (рис.7). Учитывая это, правую часть выражения (16) ещё раз умножаем на 2, тогда окончательно средняя сила тяги за пол-оборота Fт будет равна:

Fт = 16mω² ℓ ∙ cos³(π/4) ∙ sin²(π/4).                                                                         (17)

 

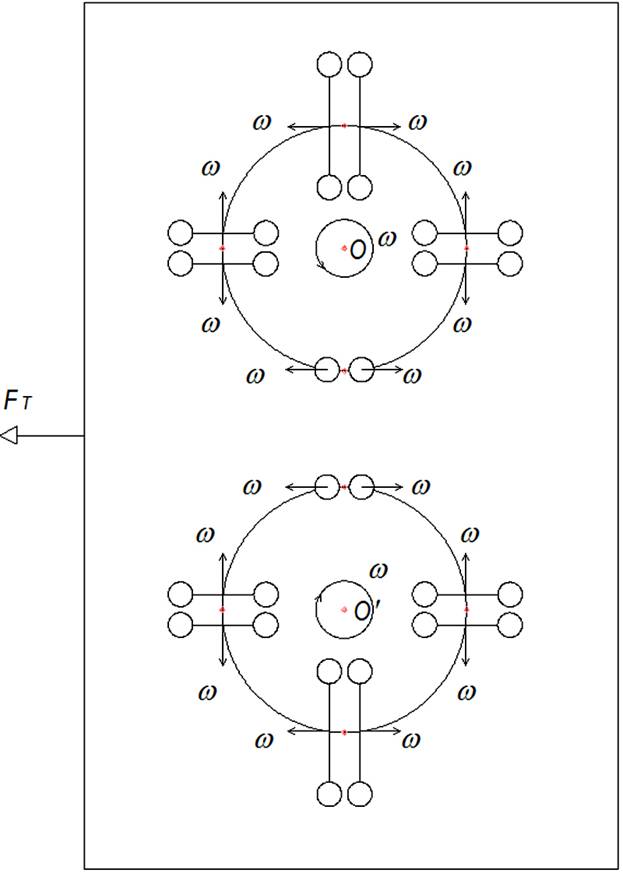
Рис. 7.

 

Пусть m = 0,1кг; ω =2πf, где f = 10об/с; ℓ = 0,5м, тогда Fт ≈ 556Н.

 

§3. Гироскоп. Кориолисова и центробежная сила инерции.

 

Рассмотрим колебательное движение груза массой m по полуокружности (рис.8) радиусом R с линейной скоростью V. Центробежная сила инерции Fц, действующая на груз массой m будет равна m V²/R.

В любой точке полуокружности центробежная сила будет по величине одинакова и направлена по радиусу от центра О. Проекция центробежной силы на ось Х будет равна

Fц׀׀ = (m V²/R) sin α.

 

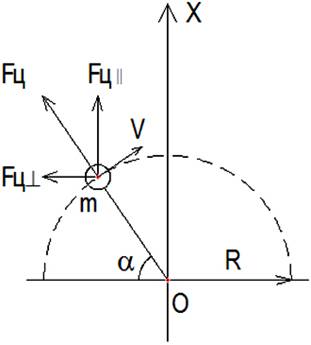
Рис. 8.

 

Из-за инертности грузов, при мгновенном изменении направления линейной скорости на противоположное, на краях полуокружности появляется обратный импульс, который препятствует поступательному движению системы в направлении оси Х.

Известно, что при воздействии силы, изменяющей направление оси гироскопа, он прецессирует под воздействием кориолисовой силы, причём это движение безинерционно. То есть при мгновенном приложении силы, изменяющей направление оси вращения, гироскоп мгновенно начинает прецессировать и так же мгновенно останавливается при исчезновении этой силы [5, 187]. Вместо груза применяем гироскоп, вращающийся с угловой скоростью ω. Теперь будем принудительно вращать ось вращения гироскопа (рис. 9) с угловой скоростью Ω. Держатель с гироскопом будет совершать безинерционное колебательное движение (прецессироавть) в определённом секторе, величина которого зависит от угловой скорости Ω. Мгновенная остановка прецессии держателя с гироскопом и возобновление её в обратную сторону происходит, когда направление угловой скорости ω проходит через перпендикуляр к плоскости рисунка (рис. 9). Таким образом, происходит колебательное безинерционное движение держателя с гироскопом, что исключает обратный импульс, препятствующий поступательному движению по оси Х.

 

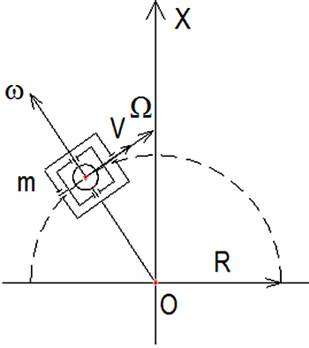
Рис. 9.

 

Для компенсации перпендикулярной проекции центробежной силы Fц_┴, как в случае с грузом (рис.8), применяем второй такой же гироскоп, совершающий колебательное движение синхронно в противофазе с первым гироскопом (рис.10). Проекция центробежной силы Fц_┴ у второго гироскопа будет направлена встречно проекции у первого. Очевидно, что перпендикулярные составляющие Fц_┴ скомпенсируются, а параллельные Fц׀׀ сложатся.

 

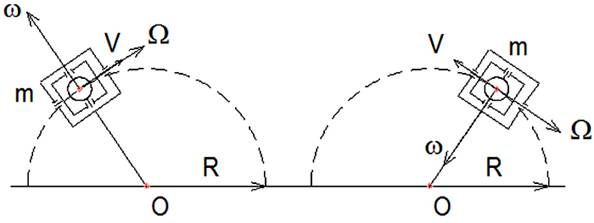
Рис. 10.

 

Если сектор колебаний грузов будет не более полуокружности, то не будет возникать противоположная центробежная сила, уменьшающая центробежную силу в направлении оси Х.

Для устранения вращающего момента устройства, возникающего из-за принудительного вращения оси гироскопов, необходимо установить ещё одну пару таких же гироскопов, оси которых вращаются в противоположную сторону. Секторы колебательного движения держателей с гироскопами в паре, оси гироскопов которых вращаются в одну сторону, должны быть симметрично направлены в одну сторону с секторами держателей с гироскопами, оси гироскопов которых вращаются в другую сторону (рис.11).

 

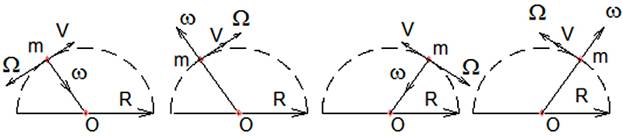
Рис. 11.

 

Вычислим среднее значение [6, 451] проекции Fц׀׀ центробежной силы для одного гироскопа (рис.8) на держателе, колеблющегося в секторе полуокружности от 0 до π и обозначим это значение через Fп

                         π

Fп = (1/ (π -0)) ∫ (m V²/ R) sin α dα = 2m V² / Rπ.                                                   (18)

                         0

Для четырёх гироскопов на держателях среднее значение поступательной силы Fп за каждый полупериод будет:

Fп = 8m V²/ R π.                                                                                                      (19)

Пусть масса держателя намного меньше массы гироскопа, а масса гироскопа m = 1кг. Линейная скорость V = 5м/с. Радиус (длина) держателя

R = 0,5м. Тогда по формуле (19) поступательная сила будет

Fп = 8∙ 1∙ 5² /0,5 π ≈ 127Н.

 

Литература

 

1.                  Курс теоретической механики: учебник / А.А.Яблонский, В.М.Никифорова. – 15-е изд., стер. – М.: КНОРУС, 2010.

2.                  С.Э.Хайкин, Физические основы механики, М.: Наука, 1971.

3.                  Справочник по физике для инженеров и студентов вузов / Б.М.Яворский, А.А.Детлаф, А.К.Лебедев. – 8-е изд.,перераб. и испр. – М.: ООО «Издательство Оникс», «Издательство «Мир и Образование», 2008.

4.                  Сивухин Д. В. Общий курс физики. Т.1. Механика. 5-е изд., стереот. – М.: ФИЗМАТЛИТ., 2010.

5.                  И.Е.Иродов, Механика. Основные законы. Учебн. пособие для вузов, 10-е изд., – М.: БИНОМ. Лаборатория знаний, 2009.

6.                  М.Я.Выгодский, Справочник по высшей математике, 14-е изд., – М.: ООО «Большая медведица», АПП «Джангар», 2001.

 

Поступила в редакцию 15.11.2011 г.