Влияние пондермоторной силы на температурные поля и напряжение в слое

 

Аббасов Зафар Думан оглы,

старший преподаватель Гянджинского государственного университета, Азербайджан.

 

Введение

 

Температурные поля и напряжения в электропроводных телах, находящихся в электромагнитном поле, обычно определяют, исходя из удель­ной мощности джоулева тепла. При этом пондермоторные силы не учитыва­ются [2, 3]. В данной работе рассматривается динамическая задача термоупруго­сти, в которой учитывается влияние пондермоторных сил и связанность полей деформации и температуры. Термоупругие постоянные материала принимаются постоянными.

Пусть на верхнем слое  имеет место конвективный теплообмен с внеш­ней средой, температура которой равна начальной температуре  слоя, нижнее основание теплоизолировано. Примем, также, что основание  сво­бодно от силовой нагрузки, а при  переменный  равен нулю. Полагая , приходим к решению системы уравнений [2, 3].

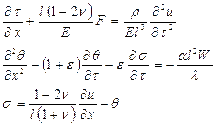                                                                            (1)

при начальных                                             (2)

и граничных условиях                              (3)

                                                                                              (3¹)

Здесь через  обозначаются безразмерные координаты отношения к тол­щине слоя , кроме того приняты обозначения: – откло­не­ние температуры от начального. – нормальные напряжения в нап­рав­ле­ние оси ;  коэффициенты теплопроводности, температуропро­вод­ности и теплоотдача на основание слоя  – коэффициент линейного рас­ши­ре­ния;  – модуль упругости и коэффициент Пуассона, – плотность мате­риала слоя; – пондермоторная сила, -удельная мощность джоилова те­пла.  и  считаются постоянными величинами;  – параметр свя­занности.

В рассматриваемом случае нормальные напряжения  и  определя­ются формулами                                                                                       (4)

где                                                                                                      (5)

Подставляя значение  из третьего уравнения в (1) получим систему урав­нений относительно функций  и .

 ,                                       (6)

Здесь приняты обозначения ,   - скорость распространения продольных волн. Решение сис­темы (6) должно удовлетворять начальные условия.

                                                     (7)

и граничные условия (3),

                    (8)

Решение задачи (6)-(8) будем искать в виде суммы по степеням коэффици­ента связности :

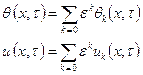                                                                                              (9)

Подставляя (9) в (6) получим:

 ,

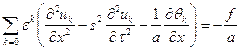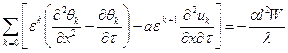
Сравнивая коэффициенты при одинаковых степенях , будем иметь сле­дующую систему начально-краевых задач:

 ;                     (А₀)

 ;                         (Б₀)

;

                                             (А₁)

 ;                                (Б₁)

а при  и  должны быть решениями следующих краевых задач:

 ;               (А_к)

 ;                            (Б_к)

В задачах  начальные и граничные условия получены при подстановке (9) в (2), (3) и (3¹).

Как видно из системы полученных задач учет связаности температурных и деформацонных полей появлается в системах задач при .

Полученные задачи будем решать методом разделения переменных. Реше­ние задачи  этим методом будет

                                                                                 (10)

где  являются корнями транецендентного уравнения.

 или                                                                          (11)

и принято обозначение

 ;

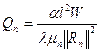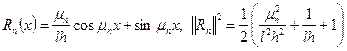
Подставляя значение (10) в задаче , отыщем . Для этого вначале граничные условия приведем к однородным

Введем функцию ,                                (12)

Подставляя (12) в задаче , получаем задачу для определения функции .

 ;

Решение задачи  представим в виде

                                                                 (13)

Для определения функции  подставляем (13) в уравнение и умно­жаем уравнение в задаче  на  и проинтегрируем полученное равен­ство в отрезке . Учитывая ортогональность функций  при этом, полу­чим: , здесь учтена фор_­­мула

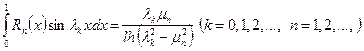
Общее решение этого уравнения представляется в виде:

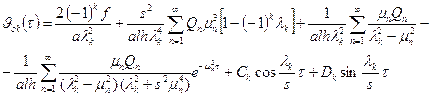                      (14)

где  произвольные постоянные, которые определяются при по­мощи начальных условий задачи :

 

Подставляя значения  в (14) результат (13) определяем

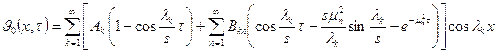     (15)

Теперь при помощи (15) и для значения  из (12) получаем решение задачи :

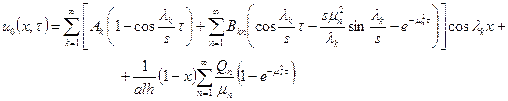  (16)

где приняты обозначения:

;

Решение задачи  представим в виде  где  - есть решение уравнения: 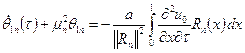                                                        (17)

Подставляя значение  из (16) в правую часть (17) и удовлетворяя начальному условию  определяем

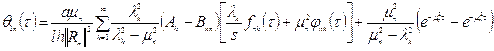      (18)

где       

Подставляя (18) в (17) получаем решение задачи

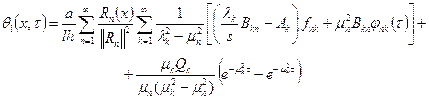                      (19)

Решение задачи  связано с задачей определения функции  при помощи формулы                                                                (20)

где  является решением задачи с однородными кривыми условиями:

,  (Д₁)

  определяется формулой

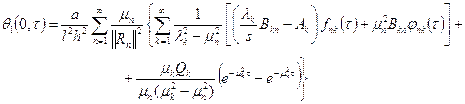                         (21)

Собственные функции задачи  образуют ортогональную систему , а собственные числа есть  Поэтому решение задачи  представим в виде:                                                                                                (22)

где  определяется уравнением:

Произведя интегрирование по частям, последнее равенство перепишем следующим образом

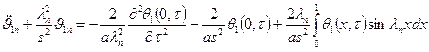
Подставляя (19) в правую часть последнего равенства и проделывая необхо­димые вычисления, получаем общее решение, в которое входит сумма  Здесь произвольные постоянные определяются началь­ными условиями  Следовательно, найденное  подстав­ляя в (22) и находим значение искомой функции  определяется согласно фор­мулой

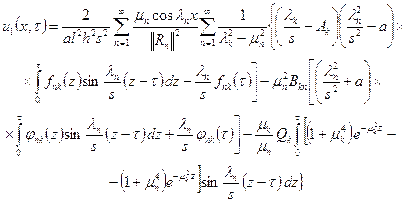
Пренебрегая членами в (9) содержание  приближенно можно опреде­лить

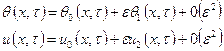                                                                         (24)

Учитывая (5) в третьем уравнении и используя полученные формулы для переменных и температуры можно записать приближенную для компонента напряжения :

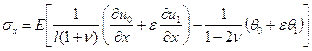                                                   (25)

а другие компоненты напряжений определяются по формулам (4):

                                                            (26)

где  

В случае рассмотрение несвязанной задачи термоупругости имеем фор­мулы (10) и (16). Из приведенных формул видно, что значения поля перемеще­ний и температуры, а также компонентов напряжений зависят от джоулева те­пла и пондермоторной силы. Исследования температурных толей и напряже­ний проводились для слоя из стали Х18Н9Т, характеристики материала ко­торых принимались равными   вт/м.град; м²/сек, , Н/м²,   м.

 

Заключение

 

Полученные числовые значения показывают, что распреде­ление напряжений и температурных полей практически совпадают для всех значений . Построены графики для напряжений  и температурного поля .

 

Литература

 

1.                  Коваленко А.Д. Основы термоупругости. Киев, «Наука думка», 1970.

2.                  Бурак Я.И., Гачкевич А.Р. О влиянии периодического во времени электромаг­нитного поля на температурные поля и напряжения в электро­проводном слое // Прикладная механика, №7, 2004.

3.                  Родигин Н.М. Индукционный нагрев стальных изделий токами нормальной частоты. М., Металлургия, 1996.

 

Поступила в редакцию 28.04.2011 г.