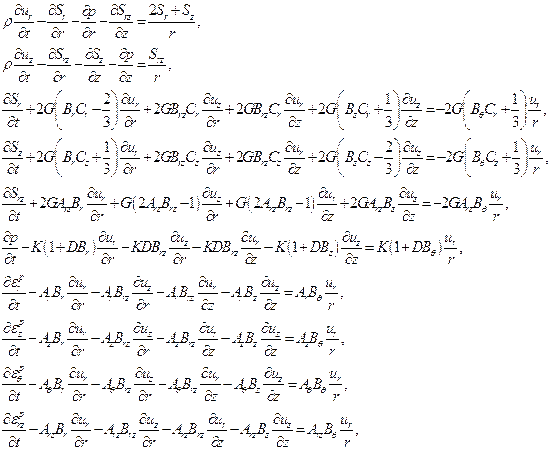Исследование поведения конструкций при сейсмических воздействиях с учетом упруго-пластических свойств материалов

Сагач Дмитрий Николаевич,

аспирант Московского государственного университета приборостроения и информатики.

Рассматриваются влияния нормальных синусоидальных динамических волн, моделирующих сейсмические явления, на поведение системы «сооружение–основание» при различных условиях воздействия. Как сооружение, так и основание представляют собой упруго-пластические тела, которые могут проявлять свойства упрочнения, разупрочнения и идеальной пластичности. В качестве определяющих соотношений для описания упруго-пластического поведения материалов сооружения и основания применялись соотношения предложенные в [1].

Задача решается в осесимметричной постановке: определим оси и обозначение границ сооружения и основания как показано на рисунке 1. Тогда уравнения движения, соотношения, вытекающие из закона Гука и ассоциированного закона, дают следующую систему дифференциальных уравнений, относительно неизвестных функций, описывающую динамическое поведение системы «сооружение–основание» [1]:

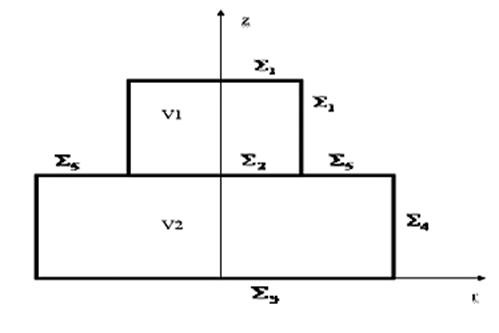
Рис. 1. Система координат.

где

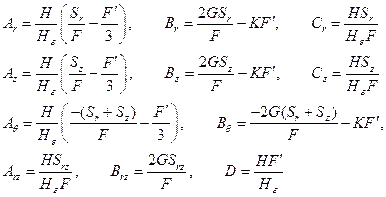
ρ – плотность, К – коэффициент объемного сжатия, G – модуль сдвига; переключатель упругость-пластичность:

,  

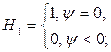
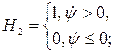
Здесь  ;  является обобщенным условием Мизеса-Шлейхера  [1]. F – функция, определяющая актуальный предел текучести:

                                                                                                   (2)

Функция упрочнения в пространстве деформаций  в рассматриваемом случае будет иметь вид:

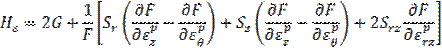                   (3)

где  - начальный предел текучести.

Положительным значениям α соответствует разупрочнение, отрицательным α – упрочнение, а при α = 0 имеет место идеальная пластичность.

В качестве начальных и граничных условий для компонент скоростей ,, девиатора напряжений ,, давления p и пластических деформаций ,,, принимается:

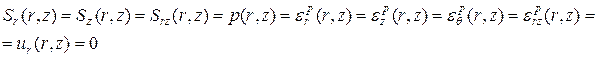 при ,

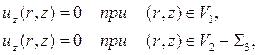
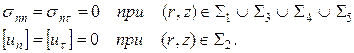
где  - область, занятая сооружением и основанием, индекс n означает проекцию на нормаль, τ – проекция на направление касательной к границе, на которой ставятся граничные условия, квадратные скобки обозначают скачок заключенной в них величины.

В качестве граничных условий рассмотрим следующие случаи:

1 случай («нижняя» волна):

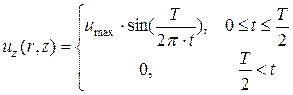 при

2 случай («сильная нижняя» волна):

, при

где  - амплитуда скорости.

Проведены многочисленные расчеты для различных вариантов сейсмического нагружения. Система (1) была численно проинтегрирована модифицированным методом конечных элементов. Получены детальные картины распределения зон разрушения и пластичности в различных слоях основания и сооружении.

Рассматривается материал сооружения со следующими характеристиками: плотность ρ = 2500 , модуль сдвига G = 4,17 ГПа, коэффициент объёмного сжатия-расширения K = 16,67 ГПа, начальный предел текучести  = 0,3 ГПа, α = 15,8 ГПа. Материал однородного основания и верхнего слоя слоистого основания имеет следующие характеристики: плотность ρ = 3000 , модуль сдвига G = 64 ГПа, коэффициент объёмного сжатия-расширения K = 50 ГПа, начальный предел текучести  = 0,7 ГПа, α = 20,11 ГПа. Материал нижнего слоя слоистого основания имеет следующие характеристики: плотность ρ = 2500 , модуль сдвига G = 7,7 ГПа, коэффициент объёмного сжатия-расширения K = 8,4 ГПа, начальный предел текучести  = 0,04 ГПа, α = 18 ГПа.

В расчётах диаметр сооружения принимался равным 9 м, основания 18 м, высота сооружения – 6 м, высота однородного основания – 12 м, а высота каждого слоя слоистого основания – 6 м. Картины, изображенные на рисунках 2 – 5, соответствуют моменту времени равному 5 мс. Амплитуда скорости  = 120 м/с для всех рассматриваемых в статье случаев.

На рисунках 2 – 5 показаны два варианта расчётов механического поведения сооружения как на однородном, так и на двухслойном основании. Во всех рисунках использовались следующие обозначения: цифрой 1 – область сооружения, где нет пластических деформаций; 2 – область основания, где нет пластических деформаций; 3 – область, где интенсивность пластических деформаций отлична от нуля; 4 – область, где произошло разрушение. Рисунки 2 – 3 соответствуют первому и второму случаю для однородного основания, а рисунки 3 – 5 – двухслойному основанию.

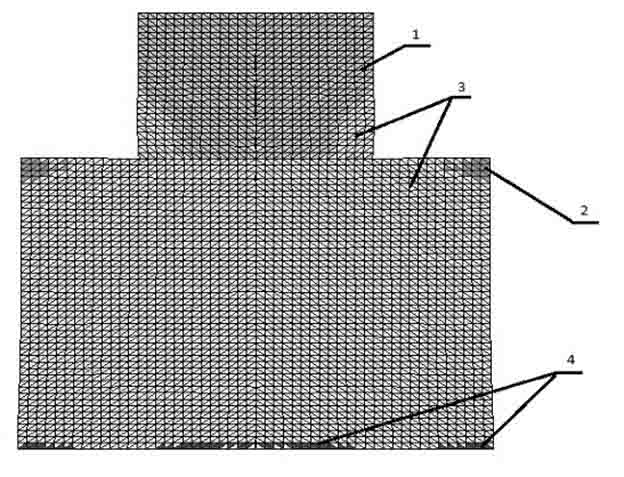
Рис. 2. Деформации сооружения и основания для однородной преграды для первого случая граничных условий.

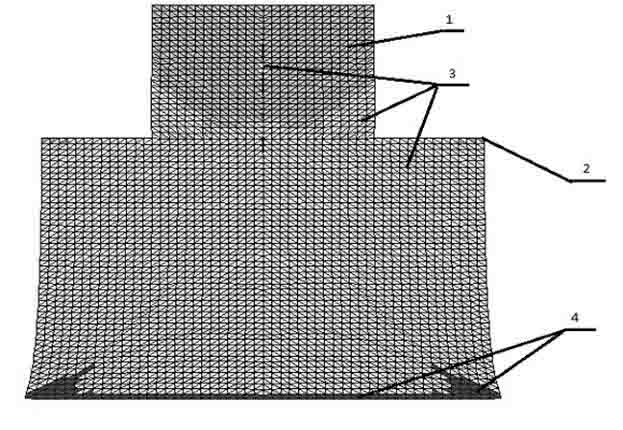
Рис. 3. Деформации сооружения и основания для однородной преграды для второго случая граничных условий.

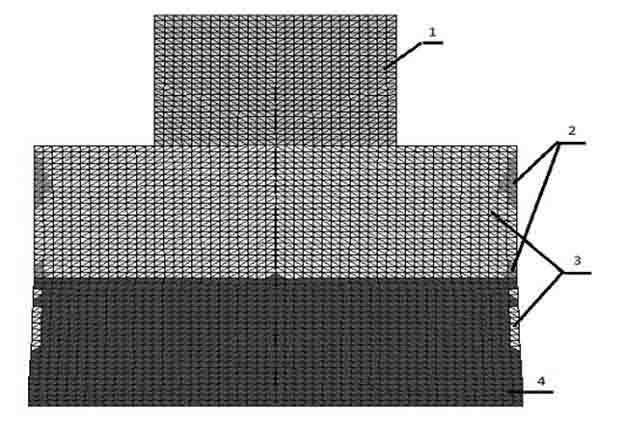
Рис. 4. Деформации сооружения и основания для слоистой преграды для первого случая граничных условий.

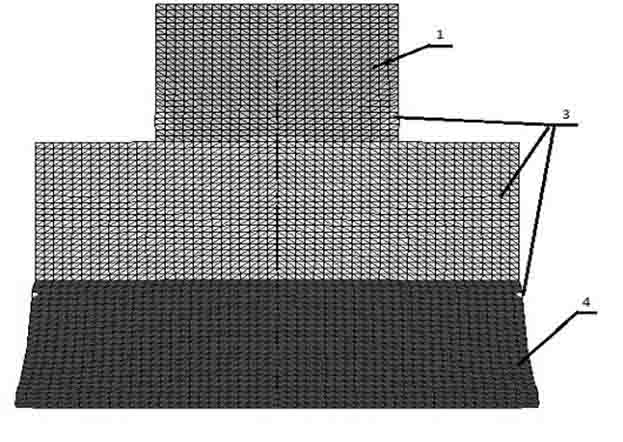
Рис. 5. Деформации сооружения и основания для слоистой преграды для второго случая граничных условий.

Сравнение результатов расчётов показывает, что введение нижнего суглинистого слоя позволяет существенно уменьшить области пластического деформирования в сооружении, а в варианте с первым случаем граничных условий и вовсе свести эту область к нулю. Данную модель можно использовать для исследования наряжено-деформированного состояния системы «сооружение-основание» для различных условий динамического нагружения. Работа выполнена при финансовой поддержке гранта Российского Фонда Фундаментальных Исследований, проект № 10-08-00425-а.

Литература

1.                Зуев В.В. Определяющие соотношения и динамические задачи для упруго-пластических сред с усложненными свойствами. - М.: ФМ, 2006. - 174 с.

Поступила в редакцию 02.06.2011 г.