Применение метода сплайн аппроксимации в фазохронометрических измерениях

Седышев Роман Владимирович,

аспирант кафедры радиоэлектроники информационных систем Уральского федерального университета.

В статье описана методика применения сплайн аппроксимации с целью определения временных параметров периодических сигналов с погрешностью меньшей периода дискретизации аналогового сигнала. Точное измерение временных характеристик периодических сигналов дает возможность определения с высокой степенью достоверности различных параметров крутильных колебаний валов в различных областях промышленности и машиностроения.

Ключевые слова: сплайн аппроксимация, индуктивный датчик, метод наименьших квадратов, фазохронометрический метод.

Keywords: spline approximation, inductive sensor, least-squares method, phase chronometry method.

Для регистрации и анализа параметров периодических процессов, происходящих в циклических машинах и механизмах, в основном применяется измерительно-диагностическая аппаратура, основанная на использовании амплитудных методов измерения. Применение таких методов обеспечивает недостаточный уровень погрешности (0.01 – 0.1 %), предъявляемый к современным системам метрологического контроля эксплуатируемой техники. Для повышения точности получаемых параметров и для понижения погрешности их определения целесообразно использование фазохронометрических методов, основанных на определении диагностических параметров функционирующих механизмов путем регистрации и анализа временных интервалов, присущих любому циклическому процессу.

Использование методов аппроксимации выходных данных датчиков обеспечивает измерение временных параметров периодических сигналов с точностью превышающей период дискретизации аналого-цифрового преобразования. Разрабатываемые алгоритмы аппроксимации находят свое применение в фазохронометрических системах измерения крутильных колебаний, скоростей вращения, осевых сдвигов и углов скручивания валов в различных областях промышленности и машиностроения.

Подобный алгоритм был разработан для определения характеризующей точки пика периодического сигнала, вырабатываемого индуктивным датчиком при вращении вала в момент прохождения алюминиевой метки на валу через ось чувствительности датчика, закрепленного перпендикулярно поверхности вала.

Выходной сигнал датчика модулируется по амплитуде и имеет форму, близкую к синусоидальной, как показано на рисунке 1.

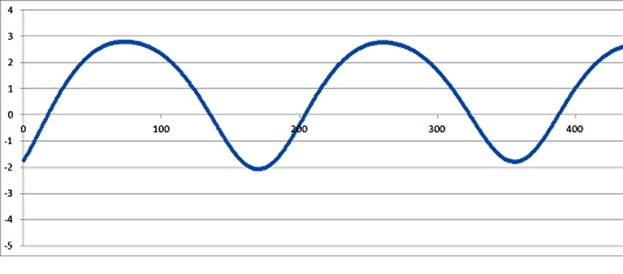
Рис. 1. Выходной сигнал индуктивного датчика.

Вклад метки в выходной сигнал индуктивного датчика можно оценить по значению площади под соответствующим пиком (над соответствующим минимумом) сигнала. Поэтому в качестве характеризующей точки пика было принято использовать абсциссу центра тяжести этого пика, который определяется площадью под пиком сигнала.

Первоначально для оценки алгоритма нахождения характеризующей точки пика был взят синусоидальный сигнал с известными параметрами. Производились многократные выборки синусоидального сигнала с различными частотами дискретизации, как показано на рисунке 2. Производился поиск центра тяжести пика для каждой выборки с целью набора статистики для определения точности нахождения характеризующей точки пика.

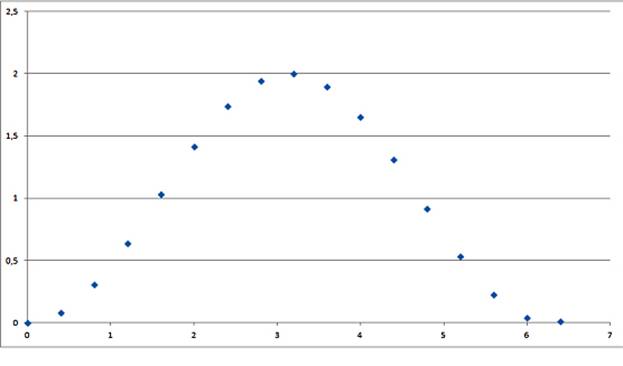
Рис. 2. Выборка синусоидального сигнала.

Полученные в результате выборки отсчеты соединяются гладкой огибающей, получаемой в результате выполнения кубической сплайн аппроксимации (рисунок 3).

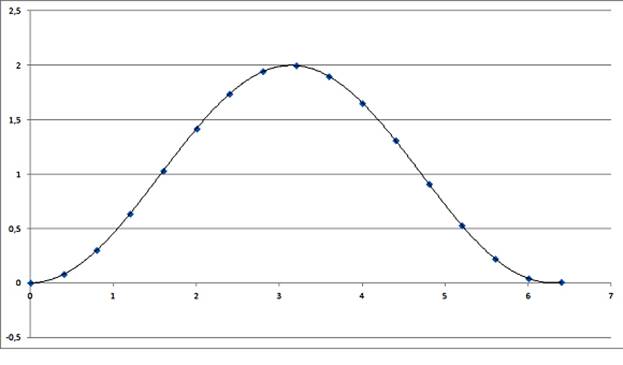
Рис. 3. Кубическая сплайн аппроксимация синусоидального сигнала.

Рассчитываются граничные точки пика – минимумы графиков сплайн-функций. После чего рассчитывается площадь под графиком путем интегрирования сплайн функций на отрезке между соответствующими соседними отсчетами сигнала. После этого определяется точка t_i на оси абсцисс, соответствующая половине площади S_1/2 под графиком. Данная точка t_i и является однозначно характеризующей точкой пика сигнала (рисунок 4).

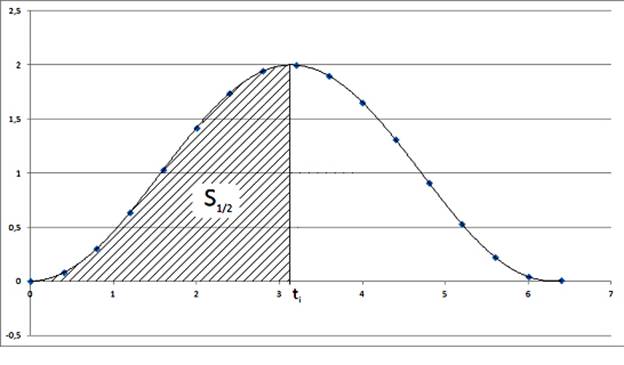
Рис. 4. Половина площади под пиком синусоидального сигнала.

Таким образом, обрабатывая по приведенной методике периодический выходной сигнал индуктивного датчика, будет получен массив характеризующих точек пиков сигнала на временной оси, которые соответствуют моменту прохождения каждой меткой оси чувствительности датчика. На основании полученных данных и при использовании определенных алгоритмов расчета могут быть рассчитаны такие параметры крутильных колебаний вала, как скорость вращения, осевые сдвиги и углы скручивания.

Подобная методика позволяет определять среднюю точку пика синусоидального сигнала с погрешностью порядка 10^-5. Величина погрешности зависит от частоты дискретизации выходного сигнала датчика и от вклада шумов в результирующий сигнал. При снижении частоты дискретизации и увеличении шумовой составляющей погрешность определения характеризующих точек пиков сигнала будет возрастать.

Поступила в редакцию 17.02.2012 г.