Общая краевая задача для уравнения третьего порядка с разрывными коэффициентами
Балкизов Жираслан Анатольевич,
научный сотрудник НИИ прикладной математики и автоматизации Кабардино-Балкарского научного центра РАН, г. Нальчик.
The boundary value problem for equation of the third order with singular operator in hyperbolic area.
Balkizov Zh.A.(Nalchik, KBSU).
В данной работе доказывается существование и единственность решения краевой задачи для уравнения третьего порядка с кратными характеристиками. Единственность решения задачи устанавливается методом интегралов энергии, а существование методом эквивалентной редукции к интегральному уравнению Фредгольма второго рода.
Ключевые слова: уравнение Геллерстедта, уравнение Фредгольма, задача Коши, уравнение Абеля, производная Капуто.
Abstract. In this paper to prove the existence and uniqueness of the solution the boundary problems for equation of the third order with multiple characteristics. The uniqueness of the solutions the problems to statement by method of integral energy. The existence of solution the problem follows from the fact that its can be reduced to an equivalent Fredholm integral equation of the second kind.
Keywords: uniqueness , existence, conditions.
Рассматривается уравнение
(1)
где 
функция Хевисайда, 
, в конечной области 
плоскости переменных 
, ограниченной при 
отрезками 
прямых 
соответственно, и
характеристиками 
и
уравнения
(1) при 
,
выходящими из точек 
и
.
Обозначим 
, 
, 
интервал прямой 
, 
.
Локальные и
нелокальные краевые задачи для уравнения (1) при 
были изучены в работе [1].
Определение.
Под регулярным решением уравнения (1) в области 
будем понимать решение из класса
.
Задача.
Найти регулярное в области решение 
уравнения (1), непрерывное в 
, удовлетворяющее
краевым условиям
(2)
(3)
Справедлива следующая теорема.
Теорема.
В области не
может существовать более одного решения задачи (1) – (3), если выполнены
следующие условия на коэффициенты 
, 
и 
:
, 
где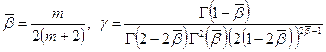 
.
Доказательство.
Введем обозначения 
.
Регулярное решение задачи Коши для уравнения (1) в области 
представимо в виде [2, с. 265]
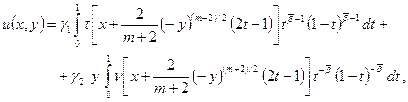(4)
где 
.
Удовлетворяя (4) краевому условию (3), получим
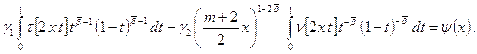(5)
В равенстве
(5) сделаем подстановку 
, а затем заменим 
на 
. Будем иметь
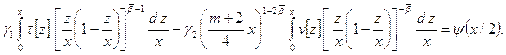(6)
После некоторых упрощений равенство (6) перепишется в виде
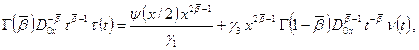(7)
где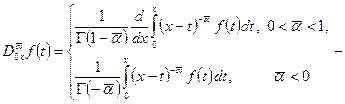 
оператор дробного
интегро – дифференцирования Римана – Лиувилля порядка 
.
Определение производной дробного порядка Римана – Лиувилля и ее основные свойства приводится в монографиях [3, стр. 13], [4, стр. 13].
Обращая (7),
как обобщенное интегральное уравнение Абеля относительно 
, получим
(8)
где 
Используя свойство композиции дробной производной и дробного интеграла с одинаковыми началами [3, стр. 27], из равенства (8) получим
(9)
Соотношение
(9) есть основное функциональное соотношение между 
и 
принесенное из гиперболической части 
области на линию 
.
Учитывая
однородные краевые условия, и, используя определение дробной производной Капуто
порядка 
[4,
стр. 14]
,
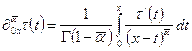соотношение (9) перепишется в следующей форме
(10)
Рассмотрим далее интеграл вида
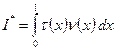. (11)
Подставим
значение 
из
(10) в интеграл (11). Будем иметь
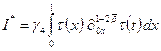. (12)
Для дальнейшего рассуждения воспользуемся следующим свойством дробной производной [5]
. (13)
С учетом (13) из (12) получается неравенство
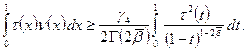(14)
Далее
перейдем в уравнении (1) к пределу при 
. С учетом граничных условий (2), получим
функциональное соотношение между 
и , принесенное из области 
на прямую 
:
(15)
(16)
Умножим обе
части равенства (15) на и проинтегрируем полученное равенство по 
от 
до 
. В результате, с учетом однородных
граничных условий, получим
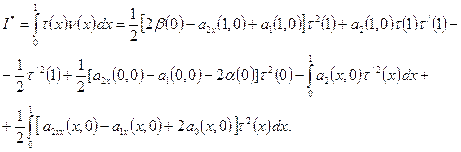(17)
С учетом (17) неравенство (14) примет вид
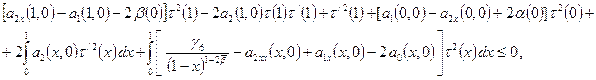где
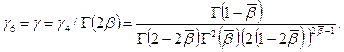
В силу
условий наложенных на коэффициенты , и , последнее неравенство может иметь
место только в том случае, когда 
.
Далее,
предполагая существование регулярного решения уравнения (1), умножим его скалярно на функцию 
где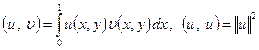 
.
С учетом
однородных краевых условий (2) 
, получим тождества
.
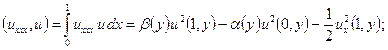
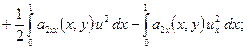
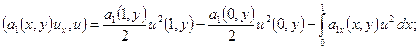
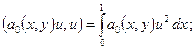
Путем почленного сложения приведенных тождеств легко убедиться в том, что
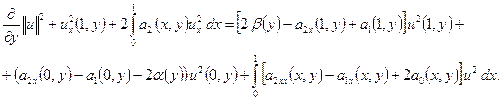(18)
Интегрируя
равенство (18) по переменной 
в пределах от 0 до , получим
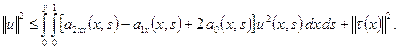(19)
В силу
условий, наложенных на коэффициенты 
выражение 
будет ограничено некоторым числом 
. Тогда из (19) имеем
оценку:
Применяя к последнему неравенству лемму 1.1 из [6, с. 152], окончательно получаем оценку:
,
где 
некоторая постоянная,
зависящая от 
.
Так как 
,
то из полученной оценки вытекает, что 
в 
. Далее из равенства (14) заключаем,
что 
.
Тогда в области 
решение
, как решение
однородной задачи Коши. Следовательно, 
в области .
Перейдем к
доказательству существования решения задачи. Пусть заданные функции 
, а 
.
Исключая из
соотношений (9) и (15) функцию , с учетом граничных условий (16), получим
краевую задачу для обыкновенного интегро – дифференциального уравнения третьего
порядка
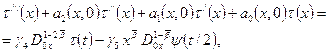(20)
(21)
С помощью элементарных преобразований уравнение (20) можно привести к следующему виду
(22)
где 
выражаются через
заданные функции 
Трижды интегрируя уравнение (22) от 0 до x, с учетом краевых условий (23), получим интегральное уравнение Фредгольма второго рода:
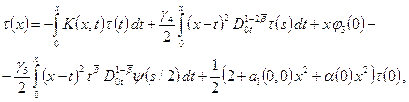(23)
где 
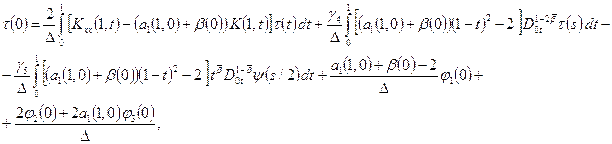
Ядро 
уравнения (23) имеет
интегрируемую особенность, а ее правая часть непрерывна на 
. Безусловная и однозначная
разрешимость интегрального уравнения (23) следует из единственности решения.
После того как из уравнения (23) найдена 
функцию 
можно найти из соотношений (9) или (14).
Тогда в области 
решение
задачи Коши определяется по формуле (5), а в области 
приходим к задаче (1), (2) и 
, исследованной в
работе [7].
Литература
1. Балкизов Ж.А. Локальные и нелокальные краевые задачи для уравнения смешанного типа третьего порядка с оператором Трикоми в гиперболической части // Вестник СамГТУ, серия «Физ. – мат. науки», №2 (17) – 2008 г. – с. 21 – 28.
2. Бицадзе А.В. Уравнения смешанного типа. – М.: Изд-во АН СССР, 1959. – 164 с.
3. Нахушев А.М. Элементы дробного исчисления и его применение. Нальчик, КБНЦ РАН, 2000. – 299 с.
4. Псху А.В. Уравнения в частных производных дробного порядка. М., 2005.
5. Алиханов А.А. Априорные оценки решений краевых задач для уравнений дробного порядка // Дифференц. уравнения. 2010 г. – Т. 46, №5. – с. 658 – 664.
6. Ладыженская О.А. Краевые задачи математической физики. – М.: Наука. – 1973. – 407 с.
7. Абдиназаров С. Общие краевые задачи для уравнения третьего порядка с кратными характеристиками // Дифференц. уравнения. 1981 г. – Т. 17, №1. – с. 3 – 12.
Поступила в редакцию 06.02.2012 г.