Аппроксимационный подход в задачах механики трещин: полиномы Чебышева в приближенном расчете сингулярных интегралов. Часть 1

НА ГЛАВНУЮ

Мовчан Игорь Борисович,

кандидат геолого-минералогических наук, доцент Санкт-Петербургского государственного горного университета.

По определению [1], полином Чебышёва первого рода n-го порядка имеет вид:

(1.1)

откуда . Рекуррентные формулы и ортогональные свойства полинома следуют из некоторых тригонометрических соотношений. Так из равенства

(1.2)

следует

, (1.3)

то есть , , и т.д. Из отношения:

, (1.4)

где или , полагая при этом

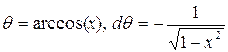, (1.5)

можно получить:

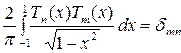
. (1.6)

В частном случае, при

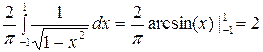. (1.7)

В связи с соотношениями (1.6), (1.7) утверждаем для любой функции, определенной на интервале , возможность следующего полиномиального разложения:

. (1.8)

Тогда для интеграла (1.6) с учетом (1.7) имеем

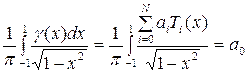. (1.9)

С другой стороны, рассматривая сумму значений в узлах 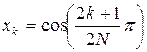, представляющих корни уравнения , получим:

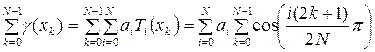, (1.10)

а используя следующее тождество:

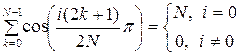, (1.11)

имеем

(1.12)

и известную формулу Эрмита:

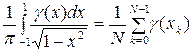. (1.13)

Формула (1.13) представляет частный случай интегрирования методом Гаусса и дает достаточно точный результат для полинома порядка меньше или равного . Используя формулу Эрмита для произведения функции на полином Чебышёва первого рода произвольного порядка

, (1.14)

получим выражение для всех коэффициентов Чебышёвского полиномиального разложения:

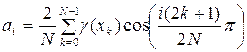, (1.15)

где и 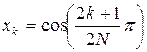. При этом использовалось тождество вида:

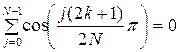при (1.16)

Значения функции на концах интервала могут быть рассчитаны по следующим формулам:

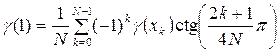, (1.17.1)

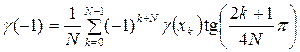. (1.17.2)

По определению [1], полином Чебышёва второго рода порядка :

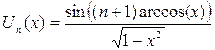, (1.18)

корни полинома порядка : 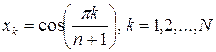. (1.19)

Без дополнительного обоснования, подобного (1.2), введем рекуррентную формулу:

т.е. (1.20)

и опуская рассуждения, подобные (1.4) и (1.5), опишем ортогональные свойства как

. (1.21)

Рассмотрим приложение полиномов Чебышёва к аппроксимации сингулярных интегралов типа Коши:

. (1.22)

Очевидно, аппроксимация интеграла (1.22) возможна при замене самого интеграла на его собственное значение:

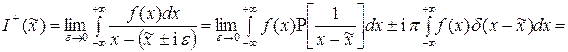
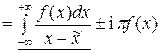. (1.23)

Заменим собственное значение в (1.23) на собственное значение интеграла типа Коши вида:

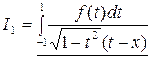, (1.24)

где - дифференцируемая функция, ограниченная на интервале . Здесь без вывода даем частный случай (24):

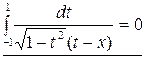. (1.25)

Кроме того, полезна формула сведения конечной суммы к отношению ортогональных полиномов го порядка:

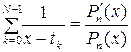, где . (1.26)

Перепишем (1.24) в виде суммы двух интегралов: регулярного и собственного значения интеграла типа Коши:

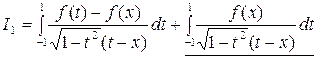. (1.27)

К первому интегралу применим формулу Эрмита (1.13), а второй интеграл сводится к нулю в силу соотношения (1.25). Окончательно, применяя формулу для конечной суммы (1.26), запишем:

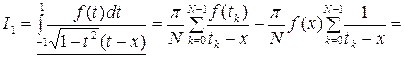
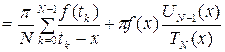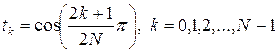(1.28)

Здесь использовалось элементарное соотношение вида . В дополнение к (1.28) приведем дополнительные формулы для полиномиальной аппроксимации интегралов типа Коши [2]:

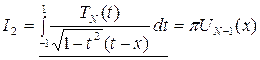, (1.29.1)

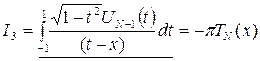. (1.29.2)

Сингулярные интегралы захватывают широкий спектр задач, в частности, обратные задачи теории потенциала и задачи расчета полей смещений, напряжений и коэффициента концентрации напряжений для разных типов трещин. Применение рассмотренного выше подхода допускает получение аналитического решения в явной форме.

Литература

1. A.Erdelyi (ed.): Higher transcendental functions. Vol.2, McGraw-Hill, NY, 1953, p.183-187.

2. F.Erdogan, G.D.Gupta: On the numerical solution of singular integral equations. Quat.J.Appl.Math., Vol.22, Jan.1972, p.525-534.

Поступила в редакцию 20.03.2012 г.