Применение теории пограничного слоя к расчету течения на речном перекате

 

Волынов Михаил Анатольевич,

кандидат технических наук, доцент, заместитель директора по науке Всероссийского научно-исследовательского института гидротехники и мелиорации им. А.Н. Костякова, г. Москва.

 

Application of the of boundary layer theory to research of river roll flow

 

M. A. Volynov.

 

Представлены результаты аналитического исследования развития пограничного слоя в потоке на речном перекате, выполненного на основе уравнения импульсов Т. Кармана. Получено приближенное решение задачи при постоянном коэффициенте сопротивления. Рассмотрена возможность более точного решения, учитывающего, изменение гидравлического сопротивления по длине переката. Оценена степень значимости произведенных уточнений.

Ключевые слова: речной перекат, пограничный слой, уравнение импульсов, изменение сопротивления, рост пограничного слоя, изменение глубины потока.

 

В пределах перекатных участков характеристики речного потока резко изменяются. От течения медленного и плавного на плесовых лощинах с большой глубиной, параметры потока постепенно приспосабливаются к новым условиям течения на перекате (уклону, шероховатости, глубине). Для расчета характеристик течения на перекате предлагается использовать теорию пограничного слоя, которая позволяет более точно учитывать изменение коэффициента сопротивления при неравномерном движении на перекатном участке речного русла.

Прежде чем переходить к детальному анализу течения на перекате, установим тип кривой свободной поверхности при переходе потока из плесовой лощины на перекат. При уклоне дна на перекате i > 0, рассматривая случай спокойного течения на перекате и, естественно, на плесе, имеем на перекате i < i_кр и h > h_кр. В зависимости от режима уровней ниже переката (глубина в конце переката h больше или меньше нормальной глубины) на перекате возможна кривая спада либо кривая подпора [1]. При дальнейшем анализе формирования потока на перекате будем рассматривать в качестве примера кривую спада. При расчете течения на перекате русло считаем призматическим, перекатный участок достаточно длинным, L_п >> h, и уклон дна на перекате постоянным.

В рамках предлагаемой двумерной расчетной схемы будем считать, что при входе на перекат распределение скоростей по нормали к дну равномерное (рис. 1).

 

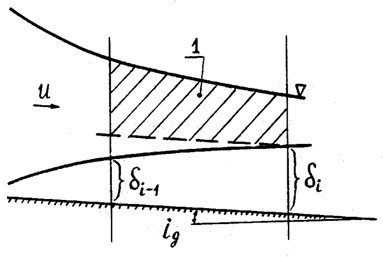
Рис. 1. Схема к расчету развития пограничного слоя на перекате. 1 – отсек внешнего течения.

 

Равномерность распределения скоростей при входе на перекат принимается с учетом малости скоростей течения и малости сил трения на подходе к перекату в пределах плесового участка и некоторого стеснения потока при входе его на перекат, что, как известно, приводит к выравниванию распределения скоростей по поперечному сечению потока.

Скорости течения вблизи дна в пределах перекатного участка уменьшаются вследствие трения жидкости о дно реки. Слой жидкости, в пределах которого заметно тормозящее действие сил трения, а тем самым и уменьшение скорости течения, называется пограничным слоем. Толщина этого слоя d увеличивается по направлению течения. Выше этого слоя течение не возмущено влиянием сил трения. Этот слой принято называть потенциальным ядром потока. Разделение потока на пограничный слой и потенциальное ядро потока в значительной степени условно. Как известно для течения с развивающимся пограничным слоем на плоской пластине справедливо уравнение импульсов Т. Кармана [2]:

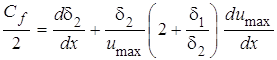,                                                                       (1)

где C_f – коэффициент гидродинамического сопротивления; d₁ – толщина вытеснения; d₂ – толщина потери импульса; u_max – скорость за пределами пограничного слоя; x – продольная координата.

Это уравнение обычно записывается для безградиентного течения в отсутствии составляющей силы тяжести и при постоянной скорости потока за пределами пограничного слоя. Для течения на перекате все указанные дополнительные действующие факторы должны быть учтены. В статье автора [2], посвященной анализу влияния этих факторов, было показано, что и в этом случае форма уравнения импульсов (1) сохраняется.

Для интегрирования уравнения импульсов необходимо иметь зависимости  и .

Следует отметить, что речные русла, как правило, работают в квадратичном режиме сопротивления [3].

Выражение для  необходимо получить в форме, удобной для интегрирования уравнения импульсов. Подходящей для этой цели формой является степенной закон сопротивления, который для квадратичного режима сопротивления может быть записан в виде:

.

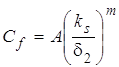Для определения коэффициента А и показателя степени m используем опытные данные разных авторов (рис. 2) по коэффициенту гидродинамического сопротивления для течения в пограничном слое на шероховатой пластине и на начальном участке шероховатых каналов.

 

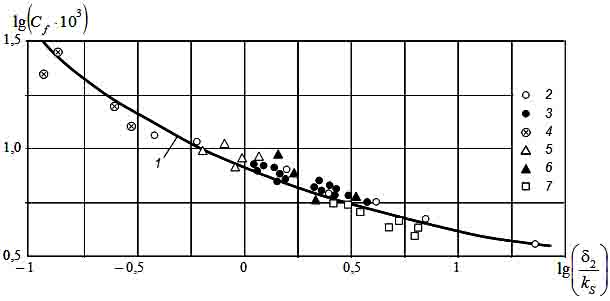
Рис. 2. Коэффициент гидродинамического сопротивления при течении в пограничном слое, на водосливе и на начальном участке канала [4].

1 — расчет по зависимости (2); 2 — данные Спена пограничный слой на шероховатой пластине; 3 — данные В. Бауэра, шероховатый водослив; 4-7 — данные В.С. Боровкова, начальный участок канала различной шероховатости (4 — k_S = 0,35 см; 6 — k_S = 0,2 см; 7 — k_S = 0,035 см).

 

Аппроксимация данных (рис. 2) может быть представлена в виде:

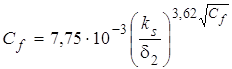.                                                                                  (2)

Далее, с учетом степенного профиля скорости

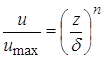
можно записать известное соотношение между толщиной потери импульса d₂ и толщиной пограничного слоя d [2] следующим образом:

,

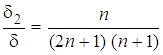которое для дальнейшего анализа можно аппроксимировать более простой зависимостью (рис. 3):

.

 

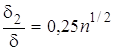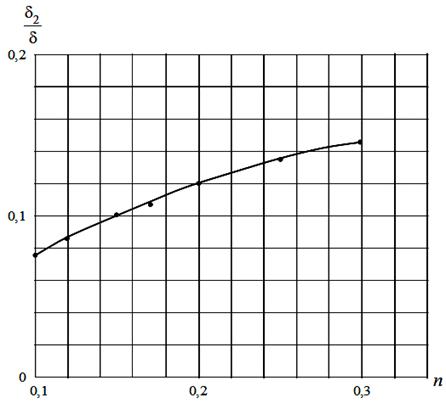
Рис. 3. К подбору апроксимации для соотношения .

 

С учетом этого соотношения выражение (2) записывается в виде:

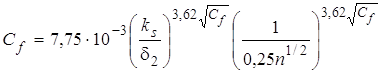.                                 (3)

Используя установленную связь между  и коэффициентом  для стабилизированного течения в широком канале [5].

                                                             (4)

и принимая во внимание, что степенной профиль скорости выполняется на участке развития течения так же, как и для стабилизированного течения, которое является заключительной фазой развивающегося течения, считаем возможным применение связи (4) для участка развития течения на перекате.

С учетом соотношения (4) множитель 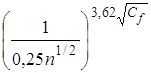 в зависимости (3) может быть аппроксимирован (рис. 4) более простым выражением:

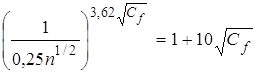.                                                                (5)

 

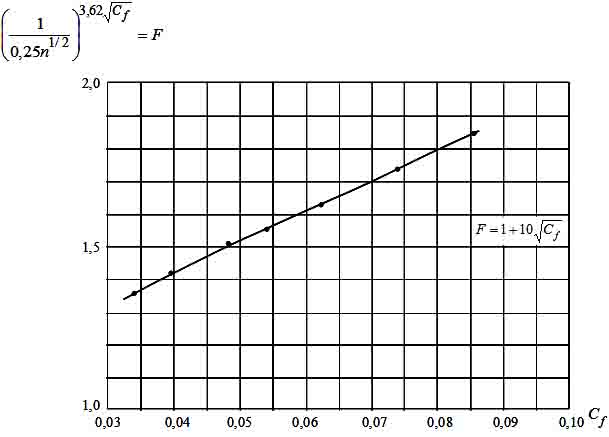
Рис. 4. Расчет функции F по выражению (5).

 

Анализ показал, что с использованием этой аппроксимации зависимость (3) можно представить (рис. 5) в следующем виде:

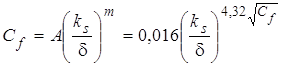.                                                          (6)

 

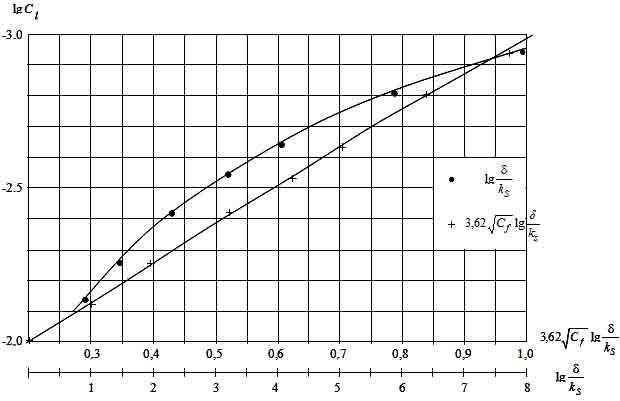
Рис. 5. Связь между коэффициентом C_f и характеристиками пограничного слоя.

 

Для определения величины 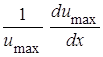, входящей в уравнение импульсов, рассмотрим условие неразрывности для пограничного слоя, которое имеет вид:

.

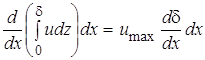Используя степенной профиль скорости и предполагая, что n можно принять приближенно постоянным на участке развития течения, запишем:

;

;

.

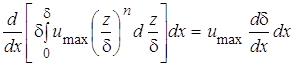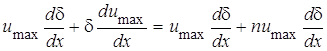Откуда находим:

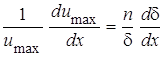.                                                                                       (7)

Заметим, что это соотношение приводит к следующей зависимости между  и d:

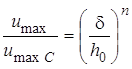,                                                                                               (8)

которая дает  при . Это является лишь следствием использован­ного граничного условия  при , поскольку вид уравнения (8) не позволяет использовать граничное условие при . Подставляя полученное соотношение в уравнения импульсов (1), запишем его следующим образом:

.

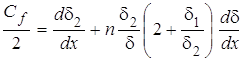уравнение импульсов при n постоянном вдоль х упрощается к виду:

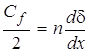.                                                                                                                      (9)

Интегрирование уравнения (9), содержащего три неизвестных величины, может быть выполнено при различных упрощающих предположениях. Первоначально рассмотрим результаты интегрирования при упрощающих предположениях  и . Используя приведенное выше соотношение (6) для  и интегрируя уравнение (9), получаем:

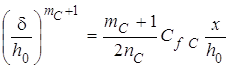,                                                                       (10)

где  — показатель степени в зависимости (6) для .

Это выражение можно записать иначе:

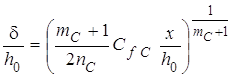.                                                                                  (11)

Полученная зависимость обнаруживает заметное влияние коэффициента гидродинамического сопротивления  на интенсивность развития пограничного слоя.

Упрощенное уравнение импульсов (9) может быть проинтегрировано численно с учетом изменения вдоль х входящих в него характеристик пограничного слоя. Результат такого интегрирования приведен на рис. 6.

 

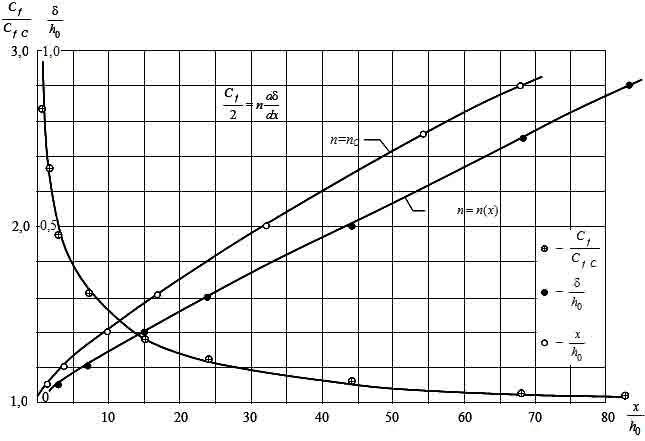
Рис. 6. Расчет пограничного слоя при n=n_C и n=n(x).

 

Сопоставляя результаты этих расчетов, приведенных на рис. 6, можно отметить заметные расхождения.

Изменение расхода в пограничном слое:

,

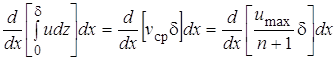где все величины ; ;  изменяются вдоль х.

Дифференцируя последнее выражение

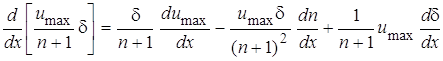
и подставляя полученное выражение в (8)

,

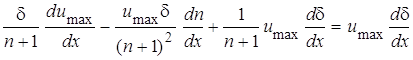откуда

;

.

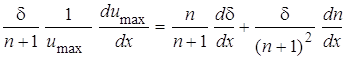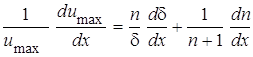Подставляя это выражение в уравнение импульсов (1), получим:

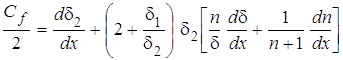.                                           (12)

Записывая связь между d₂ и d в виде

,

где

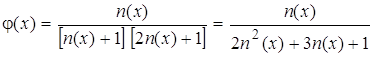.                                               (13)

Тогда

,

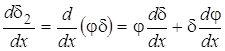где                  .

Учитывая, что

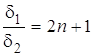 и ,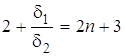

найдем, дифференцируя выражение (13)

.

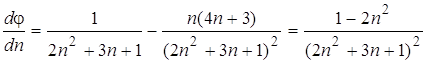Тогда

.

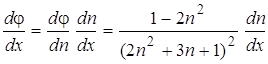С учетом полученных соотношений второе слагаемое в уравнении (12):

;

.

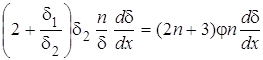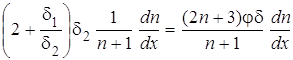Подставляя эти соотношения в (12), запишем:

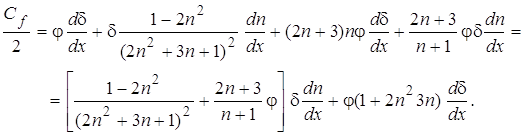 (14)

Обозначая множитель в квадратных скобках как , вычислим его величину при различных n (табл. 1).

 

Таблица 1.

n	0,10	0,15	0,20	0,25	0,30
f1	0,96	0,92	0,88	0,84	0,70

 

Расчет показывает, что для реальных значений n = 0,15÷0,25 изменения f₁ невелики и в среднем величина f₁ близка к 0,9.

Следует отметить, что при n постоянном вдоль х с учетом (13) из (14) может быть получена упрощенная форма уравнения импульсов (9).

С учетом полученных соотношений уравнение импульсов (14) приводится к виду:

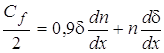.                                                                                       (15)

В этом уравнении три неизвестных: , поэтому для решения задачи необходимо использовать две независимые связи между указанными изменяющимися характеристиками пограничного слоя.

В качестве одной из таких связей используем зависимость n от коэффициента сопротивления, которая для стабилизированного течения в широких каналах имеет вид [5]:

.                                                                                                   (16)

Учитывая, что стабилизированное течение является завершающей фазой развивающегося течения и принимая во внимание соотношение между  и коэффициентом гидродинамического сопротивления C_f

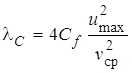,                                                                                               (17)

распространим соотношение (16) на всю зону развития пограничного слоя, записывая его в виде:

.

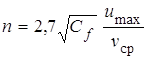Учитывая, что для широкого потока 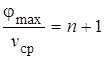, запишем

.                                                                                                (18)

Это соотношение может быть преобразовано к виду:

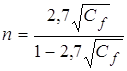.                                                                                                 (19)

В качестве необходимого третьего соотношения используем связь (6) между  и :

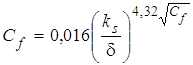.                                                                                (20)

Таким образом, имеются три уравнения: (15), (19) и (6), которые позволяют решить задачу о расчете пограничного слоя на перекате с учетом изменения показателя степени n(x) и  по мере развития пограничного слоя на перекате.

Интегрирование дифференциального уравнения (15) с использованием дополнительных соотношений (19) и (6) выполняется численно. Расчет обнаруживает резкое возрастание сопротивления на начальном участке переката, что не учитывается традиционным гидравлическим расчетом (рис. 7).

 

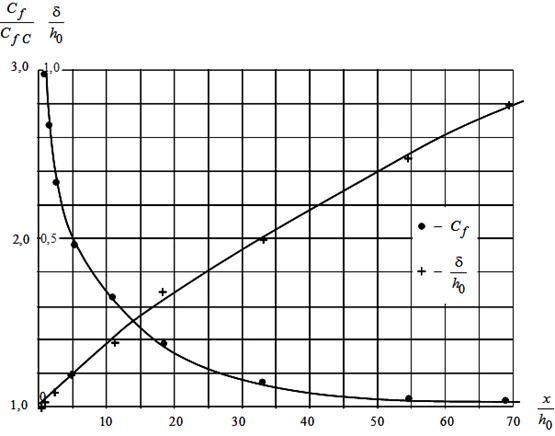
Рис. 7. Изменение коэффициента гидродинамического сопротивления и толщины пограничного слоя на речном перекате.

 

Сопоставление результатов расчета, выполненного по точному уравнению импульсов (15) при  и по упрощенному уравнению (9) при  и , обнаруживает заметные расхождения лишь при значениях х, соизмеримых с глубиной потока, где коэффициент  существенно превосходит величину . С увели­че­ни­ем х расхождения становятся незначительными, что позволяет для практи­чес­ких расчетов использовать зависимости, полученные на основе упрощен­но­го уравнения импульсов (9), в том числе формулу (11).

С использованием полученной зависимости (11) из условия d = h₀ при х = х_С может быть найдена длина участка х_в, на котором пограничный слой развивается на всю глубину потока:

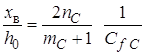.                                                                                            (21)

Тогда выражение (10) можно записать иначе:

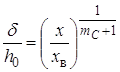.                                                                                                  (22)

Получив соотношения , можно с использованием зависимости  получить зависимость

.

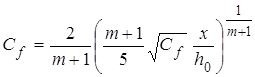Далее, выражая удельный расход следующим образом:

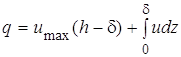
и разделив обе части равенства на , получим:

.

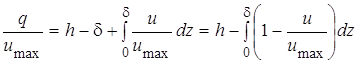Учитывая, что интеграл в правой части есть не что иное, как толщина вытеснения d₁, запишем, что

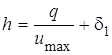.                                                                                                    (23)

Поскольку 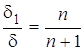, с использованием соотношений (22) и (8) найдем изменение глубины в виде:

.

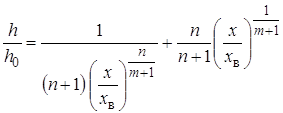Заметим, что при  это соотношение дает , что объясняется несовершенством зависимости (8) на этом пределе.

Если изменение  учесть в уравнении (23) в виде:

,                                                                      (24)

получаем следующее уравнение:

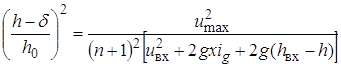,                                           (25)

дающее при  конечное значение глубины . (Во всех приведенных зависимостях считается приближенно, что n не зависит от х и равно .)

Следует различать длину , на которой пограничный слой развивается на всю глубину потока, от длины , на которой течение полностью стабилизируется . Из уравнения (24) находим:

.

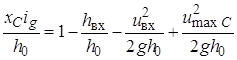Рассматривая вход на перекат как водослив с широким порогом [1], для которого:

,                                                                                                 (26)

(где  — коэффициент расхода, близкий к 0,3÷0,35) найдем с использованием формулы Шези:

,

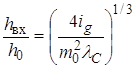где .

Тогда

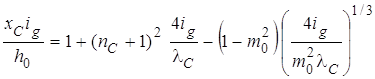.                                   (27)

Данная зависимость показывает, что длина участка полной стабилизации течения существенно зависит от условий во входном сечении.

Разработанный на основе теории пограничного слоя подход к расчету неравномерного движения может послужить основой для построения кривых свободной поверхности в водотоках, а также определения всех необходимых характеристик течения на перекатах. Полученные зависимости могут быть также использованы при расчетах характеристик течения на начальных участках широких каналов.

 

Литература

 

1.                  Справочник по гидравлическим расчетам / под ред. Киселева П.Г. М.: Энергия, 1972, 312 с.

2.                  Шлихтинг Г. Теория пограничного слоя. М.: Наука, 1969, 742 с.

3.                  Байков В.Н. Режим сопротивления речных русел // Материалы межд. научно-практич. конф. «Строительство, формирование среды жизнедеятельности». М.: МГСУ, 2003. С.

4.                  Боровков В.С. Высокоскоростные потоки со свободной поверхностью. М.: Стройиздат, 1979, 343 с.

5.                  Байков В.Н., Волынов М.А. Сопоставление гидравлических характеристик осесимметричных и плоских течений при ламинарном и турбулентном движении жидкости // Известия ВУЗов. Строительство. 2010. №9. С.100-107.

 

Поступила в редакцию 02.08.2012 г.