Теоретическая оценка температуры контактной поверхности вакуумного выключателя средних напряжений при протекании по ним сквозного тока короткого замыкания

 

Байда Евгений Иванович,

кандидат технических наук, доцент кафедры «Электрические аппараты» Харьковского национального технического университета «НТУ ХПИ».

 

Одним из требований технического задания на проектирование вакуумных выключателей средних напряжений является условие термической устойчивости. Это условие заключается в нормальном функционировании аппарата после прохождения через его контакты априори заданного тока короткого замыкания в течение определенного промежутка времени. Согласно литературе [Кузнецов Р.С.], при этом может наблюдаться сваривание контактов, сила которого начинает сказываться на работе аппарата при достижении температуры контактной поверхности значения температуры размягчения (рекристаллизации). Наибольшие значения силы сваривания возникают при нагревании контактной поверхности до температуры плавления. Как указывается в литературе [Кузнецов Р.С.], точный расчет сил сварки практически неосуществим из-за статистического характера процесса. Приближенные оценки сил сваривания, исходя из предположения о наличии расплавленной области на части контактной поверхности, были проведены в [Дашкевич А.С., Омельченко В.Т.]. Однако теоретические данные не всегда согласуются с экспериментальными, приведенными на рис.1 [Кузнецов Р.С.], из которых следует, что при токе 10 кА и контактном нажатии f =100 Н сила сваривания F₀ будет 10*f, а при f =1000 Н сила сваривания F₀ будет 0.1*f. Следовательно, во втором случае привод аппарата с легкостью разорвет сварившиеся контакты, а в первом – нет. Такое различие в значениях сил сваривания можно объяснить тем, что в случае значительных контактных нажатий сварка плавлением отсутствует за счет изменения величины контактной поверхности. Следовательно, сила контактного нажатия должна выбираться из условия f =I кА*100 Н/кА, [Кузнецов Р.С.].

 

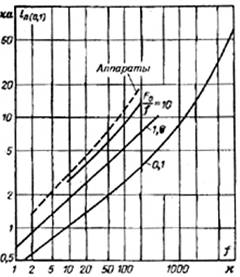
Рис. 1. Зависимость величины тока сваривания от величины контактного нажатия.

 

Сила сваривания при токе 20 кА, рассчитанная по [Дашкевич А.С., Омельченко В.Т.] для автоматических выключателей, более 2000 Н, что можно объяснить существенно меньшим, чем требуется, значением сил контактного нажатия. Как указывалось выше, расчеты в литературе [Дашкевич А.С., Омельченко В.Т.] проведены при условии существования на контактной поверхности области расплава и не описывают процесс размягчения материала и увеличения размеров контактной площадки без процесса плавления.

В этой связи, теоретическая оценка температуры нагрева контактной поверхности в зависимости от величины тока, времени его протекания и величины контактного нажатия является актуальной.

Цель работы – рассчитать температуру контактной поверхности в зависимости от величины сквозного тока короткого замыкания при заданном значении сил контактного нажатия и времени протекания тока.

Для достижения поставленной цели необходимо решить следующие задачи: 1) на основании уравнений теории упругости рассчитать значение площади контакта в зависимости от температуры контактной поверхности; 2) определить эквивалентный радиус области контакта; 3) определить температуру контактной поверхности с учетом нагрева током удаленной от контактной площадки области тела контакта.

Допущения, принятые при расчете: вид контакта – линейный; так как постоянная времени нагрева контактной поверхности невелика (10^-4 с) [Кузнецов Р.С.], то ее температура «мгновенно отслеживает» изменение температуры удаленной точки; модуль упругости является линейной функцией температуры.

Расчетная модель контактной поверхности показана на рис.2.

 

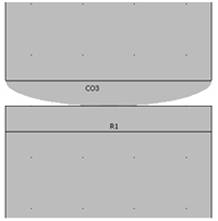
Рис. 2. Расчетная модель контактной поверхности.

 

Согласно литературе [Омельченко В.Т., Тимошенко С.П., Френкель Я.И.], расчетные уравнения теории упругости и теплопроводности в общем виде выглядят:

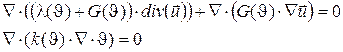                                                          (1)

где l, G – коэффициенты, зависящие от модуля упругости (который линейно изменялся в зависимости от температуры) и коэффициента Пуассона,  – вектор перемещений; k – коэффициент теплопроводности; J – температура.

Уравнения (1) должны быть дополнены условиями на границе – фиксация одной границы и нагрузка на другой, температурой на контактной поверхности и на удаленной границе. Расчет был проведен по следующей методике: при фиксированной силе контактного нажатия определялась площадка контакта и распределение удельного давления при ряде температур, задаваемых на контактной поверхности в долях температуры плавления; определялся эквивалентный радиус контактной площадки для точечного контакта, определялась температура контактной поверхности с учетом нагрева тела контактов током короткого замыкания.

Результаты расчетов удельного контактного давления в цилиндрической системе координат при силе контактного нажатия в 2000 Н в зависимости от температуры контактной поверхности для медных контактов приведены на рис.3.

 

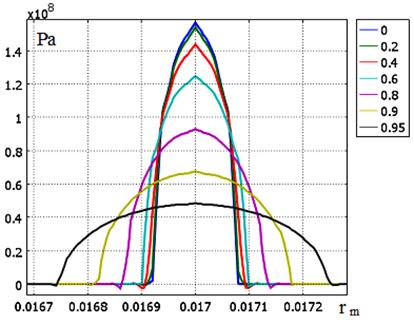
Рис. 3. Изменение радиуса площади контакта и удельного давления в зависимости от температуры контактной поверхности в долях температуры плавления.

 

На рис.4 показано распределение давления по центру контактной площадки в вертикальной плоскости.

 

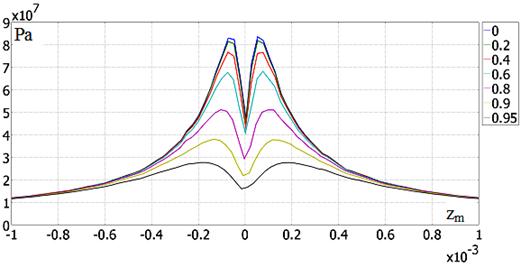
Рис. 4. Распределение давления по центру контактной площадки в вертикальной плоскости.

 

Так как в цилиндрической системе координат контактная поверхность представляет собой кольцо, то для дальнейших расчетов она была преобразована в эквивалентную круговую поверхность с радиусом a(J), изменение которого в зависимости от температуры и силы контактного нажатия приведены на рис.5.

 

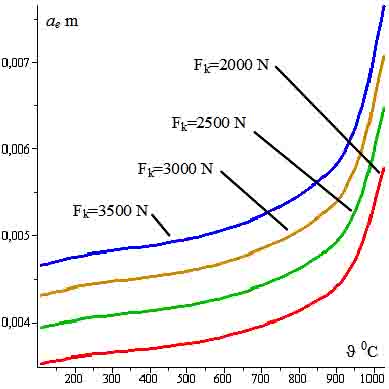
Рис. 5. Зависимость эквивалентного радиуса площади контакта от температуры контактной площадки и силы контактного нажатия.

 

Известно [Омельченко В.Т.], что в области стягивания линий тока удельное электрическое сопротивление изменяется по закону:

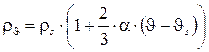                                                                                                       (2)

где r – удельное электрическое сопротивление; a – температурный коэффициент удельного сопротивления; J – температура; J_s – справочное значение температуры.

В этом случае, значение переходного контактного сопротивления будет изменяться по зависимостям, показанным на рис.6.

 

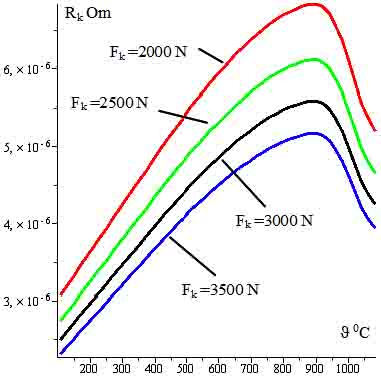
Рис. 6. Зависимость контактного сопротивления от температуры контактной поверхности и силы контактного нажатия.

 

Для определения температуры нагрева контактной поверхности воспользуемся известным уравнением [Залесский А.М.]:

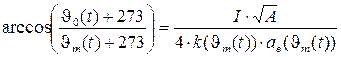                                                           (3)

где J₀(t) – температура удаленной от контактной поверхности точки; J_m(t) – температура контактной поверхности; I – действующее значение тока; A – постоянная Лоренца; k – теплопроводность; a_e – эквивалентный радиус площади контакта.

Для повышения точности расчетов теплопроводность в (3) определялась на основании закона Видемана – Франца – Лоренца:

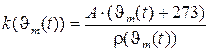                                                                                                       (4)

Для определения температуры контактной поверхности по (3), необходимо определить J₀(t) – температуру удаленной от контактной поверхности области при токе короткого замыкания. Для этого будем исходить из того, что значение сквозного тока короткого замыкания достаточно велико – 20кА, а время его протекания – 3с. В этом случае режим нагрева можно считать адиабатическим. Тогда, уравнения нагрева запишутся в виде:

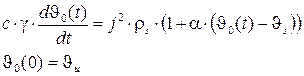                                                                       (5)

где c – теплоемкость; g – плотность материала; j – плотность тока удаленного участка; J_u – установившееся значение температуры в номинальном режиме.

Решение уравнения (5) известно:

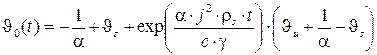                                                              (6)

Согласно литературе [Ткаченко С.А.], температура контактной системы вакуумного выключателя в длительном режиме работы равна (98-100) ⁰С. Это значение и определяет установившееся значение температуры в (6).

На основании полученных соотношений был проведен расчет температуры поверхности контактов по (3) с учетом (6) для силы контактного нажатия 2000 Н, токе 20 кА при времени его протекания 3с.

Проведенный расчет показывает, что температура контактной поверхности в этом случае составляет 290⁰С и практически равна температуре рекристаллизации, при этом 207⁰С приходятся на температуру J₀(t), что свидетельствует о существенном влияние температуры токопровода на температуру контактной поверхности в режиме протекания сквозных токов короткого замыкания.

На рис.7 показано значение температуры контактной поверхности в зависимости от тока.

 

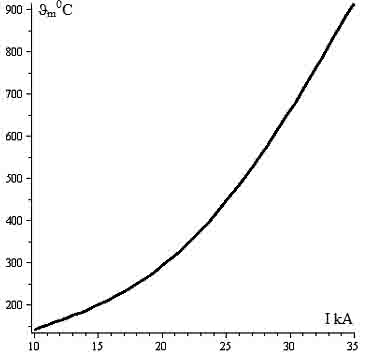
Рис. 7. Зависимость температуры контактной поверхности от сквозного тока короткого замыкания через 3 секунды при контактном нажатии 2кН.

 

Как следует из рис.7, при токах более 20 кА температура контактной поверхности существенно возрастает и при токе 35 кА достигает температуры плавления. Причем, увеличение контактного нажатия мало влияет на максимальное значение температуры контактной поверхности. На рис.8 приведены зависимости температуры контактной поверхности в функции тока при различных контактных нажатиях.

 

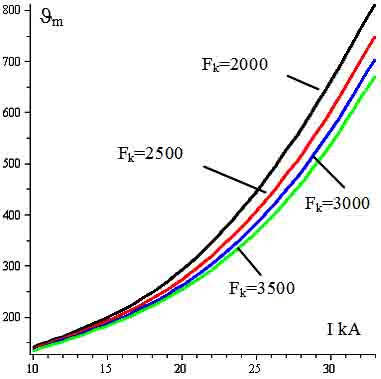
Рис. 8. Температура контактной поверхности в зависимости от тока и контактного нажатия через время 3 секунды.

 

В гораздо большей степени на температуру контактной поверхности влияет сечение токоподводящих проводников. На рис.9 показаны значения температуры контактной площадки в зависимости от диаметра тела контакта при контактном нажатии 2000 Н и токе 33кА за время 3с.

 

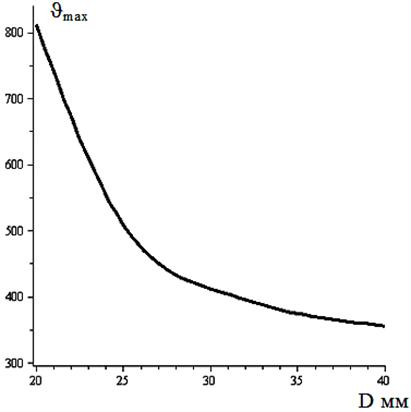
Рис. 9. Температура контактной поверхности в зависимости от диаметра токопровода при токе 33кА за время 3 секунды.

 

Выводы

 

При малых контактных нажатиях увеличение площади контакта не компенсирует рост температуры контактной поверхности. Результаты, полученные в данной работе, хорошо согласуются с экспериментальными данными (рис.1) и результатами работ [Дашкевич А.С., Омельченко В.Т.] при плавлении контактной площадки (нажатие 200 Н, ток 19 кА, сила сварки 2400 Н). На температуру контактной поверхности в режиме протекания сквозного тока существенное значение оказывает температура удаленных точек токопровода, с учетом которой и необходимо выбирать величину контактного нажатия.

 

Литература

 

1.                  Дашкевич А.С. Сваривание металлокерамических контактов при больших сквозных токах: дисс. канд. техн. наук: 05.09.01 / Дашкевич Александр Сергеевич.– Х., 1981. – 151 с.

2.                  Залесский А.М. Тепловые расчеты электрических аппаратов / Залесский А.М., Кукеков Г.А. // – Л-д., Энергия, 1973. – 379 с.

3.                  Кузнецов Р.С. Аппараты распределения электрической энергии на напряжение до 1000 В / Кузнецов Р.С.// – М.: Энергия, 1970. – 544 с.

4.                  Омельченко В.Т. Математические модели тепловых процессов в электрических контактах / Омельченко В.Т., Ким Е.И., Харин С.Н. // – Алма-Ата; Наука Казахской ССР, 1977. – 236 с.

5.                  Тимошенко С.П. Теория упругости: Пер. с англ./ Гудьер Дж., Тимошенко С.П., под редакцией Шапиро Г.С. // – М.: Наука. Главная редакция физико-математической литературы, 1979. – 560 с.

6.                  Ткаченко С.А. Оценка температуры контактной системы вакуумной камеры/ Ткаченко С.А., Жвороронков М.А. // Электротехника, – 2010. – №11. – С. 32 – 35.

7.                  Френкель Я.И. Курс теоретической механики / Френкель Я.И.// – Ленинград: Типография «Красный печатник», 1939. – 386 с.

 

Поступила в редакцию 11.03.2013 г.