Оценка реактивной мощности трехфазной нагрузки
Ясаков Геннадий Серафимович,
доктор технических наук, профессор,
Бондаренко Александр Евгеньевич,
кандидат технических наук,
Асмоловский Эдуард Федорович,
кандидат технических наук,
Крохмаль Эдуард Романович.
Санкт-Петербургский морской технический университет.
До настоящего времени ни один нормативный документ не определяет понятие «реактивная мощность» в общем случае, лишь только [2] определяет этот термин для линейной нагрузки, как взаимное произведение действующих значений напряжения и тока на синус угла между их изображающими векторами, но и из этого определения не очень понятен физический смысл.
Попробуем сделать еще одну попытку, чтобы определить физический смысл понятия «реактивная мощность». Для этого рассмотрим однофазную цепь, содержащую последовательно соединенные элементы: активное сопротивление R, индуктивность L, емкость С. Эта цепь включена на источник синусоидального напряжения u, в цепи протекает установившийся синусоидальный ток i,
u = iR + L di/dt+ ∫ idt/C.
После подстановки в это уравнение выражений для u и i получим:
Um sinωt = R Im sin(ωt – φ) + Im (ωL – 1/ωC) cos(ωt – φ), (1)
где: Um - амплитуда синусоидального напряжения или модуль изображающего вектора напряжения, Im - амплитуда установившегося синусоидального тока или модуль изображающего вектора тока, di/dt - производная от мгновенного тока i, φ - фазовый сдвиг между синусоидами тока и напряжения или фазовый сдвиг между изображающими векторами напряжения и тока, ω – угловая частота.
Полученное уравнение (1) возведем в квадрат, а затем определим среднее, интегральное значение на интервале времени, равном периоду питающего напряжения:
U2 = I2 R2 + I2 (ωL – 1/ωC)2,
где: U-действующее значение синусоидального напряжения, I –действующее значение установившегося синусоидального тока.
Теперь умножим это уравнение на величину квадрата действующего значения тока, в результате получим известное выражение для полной, или кажущейся мощности S:
S2 = U2 I2 = I4 R2 + I4 (ωL - 1/ωC)2 = P2 + Q2 = (UI cos φ) 2 + (UI sin φ) 2
где;
P и Q – соответственно активная и реактивная мощность .
Данный подход позволяет определить только средне интегральные энергетические характеристики S, Q, P линейной цепи за период питающего напряжения.
Рассмотрим теперь мгновенные энергетические процессы в этой же цепи, для этого умножим выражение (1) на величину установившегося мгновенного тока, в результате получим:
ui =UI(cosφ - cos(2ωt- φ) = I2R(1+cos(2ωt- 2φ))+I2(ωL- 1/ωC)sin(2ωt - 2φ),
где: p(t) = ui – мгновенная мощность цепи, которая может принимать как положительные так и отрицательные значения (рис.1), а ее действующее значение равно активной мощности P.
pr(t) = I2R(1+cos(2ωt- 2φ)) – мгновенная активная мощность, совершающая работу, не принимает отрицательные значения (рис.1), ее действующее значение также равно активной мощности P.
q(t) обм = I2(ωL- 1/ωC)sin(2ωt – 2φ) – мгновенная обменная мощность, между источником и потребителем, она не совершает никакой работы (рис.1), если не считать дополнительных потерь в линиях связи, принимает отрицательные значения в момент отдачи накопленной энергии и положительные в момент накопления энергии). Действующее значение мгновенной обменной мощности q(t)обм равно нулю (рис.1).
В каждый момент времени энергия емкости определяется как:
WC(t) = 0.5Сuc2 = 0,5ω-2С-1I2(1+ cos(2ωt – 2φ)),
а мгновенная, накопленная энергия индуктивности равна:
WL(t) = 0.5i2L = 0,5LI2(1- cos(2ωt– 2φ)).
Очевидно, что мгновенная обменная мощность является производной от суммарной накопленной энергии в реактивных элементах:
q(t) обм = d(WC(t) + WL(t)) /dt
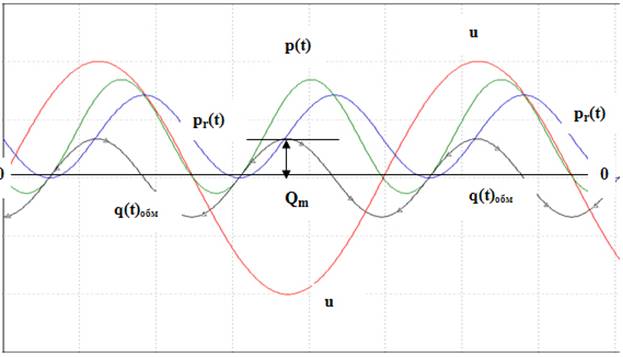
Рис. 1. Мгновенные энергетические процессы в линейной, однофазной цепи.
Можно заметить, что амплитуда Qm мгновенной обменной мощности (рис. 1) равна разности действующих значений накопленной энергии индуктивности и емкости, умноженной на удвоенную угловую частоту, а также амплитуда Qm равна общепринятой реактивной мощности :
Qm = I2(ωL- 1/ωC) = 2ω[0,5I2(L - ω-2С-1]= Q= UI sin φ.
Причиной возникновения мгновенной обменной мощности, для данной цепи, является наличие индуктивности и емкости, в этих элементах электромагнитная энергия накапливается, а затем, разряжаясь, направляется в источник, эти процессы вызывают фазовый сдвиг между изображающими векторами тока и напряжения.
Итак, для рассмотренной выше линейной цепи, понятие «реактивная мощность» связано с накопленной электромагнитной энергией в реактивных элементах. Величина реактивной мощности Q пропорциональна действующему значению накопленной электромагнитной энергии за период, а коэффициент пропорциональности равен удвоенной угловой частоте.
Рассмотрим теперь мгновенные энергетические процессы при включении трехфазной нагрузки, элементами которой являются активное сопротивление R и индуктивность L, соединенные последовательно для каждой их трех фаз:
ua = iaR + L dia/dt,
ub = ibR + L dib/dt, (2)
uc = icR + L dic/dt.
Умножим эти уравнения на соответствующий мгновенный фазный ток, а после взаимно сложим, в результате получим:
p(t) = uaia + ubib + ucic = 1,5 (Im)2R+qa(t) обм+qb(t) обм+qc(t) обм , (3)
где: p(t)- мгновенная мощность трехфазной нагрузки, Im – мгновенный модуль изображающего вектора тока трехфазной нагрузки, здесь величина не постоянная, в отличии от предыдущего примера, qa(t) обм, qb(t) обм, qc(t) обм – мгновенные, обменные мощности фаз.
Сумму мгновенных обменных мощностей по фазам можно записать как мгновенную обменную мощность трехфазной нагрузки:
q(t)обм = qa(t) обм + qb(t) обм + qc(t) обм = d(0,75L Im2)/dt.
Эта мгновенная обменная мощность q(t)обм равна нулю, при установившихся фазных токах линейной нагрузки, так как производная от квадрата модуля тока или производная от мгновенной накопленной электромагнитной энергии в трех индуктивностях также равна нулю. При этом существуют фазные, мгновенные обменные мощности, но между источником и потребителем обменные процессы не наблюдается. В переходном режиме, при включении трехфазной нагрузки, сумма мгновенных обменных мощностей уже не равна нулю.
Выражение мгновенной мощности, для рассматриваемого случая, можно записать в виде [1, 5]:
p(t) = 1,5 (Im)2R + 0,75Ld(Im2)/dt.
Теперь каждое уравнение из (2) умножим соответственно на «1», «exp(j120)», «exp(j240)», в результате получим комплексное, векторное уравнение активно-индуктивной трехфазной нагрузки:
Umexpj(γ+ β+φ) =Im R expj(γ+β) +LI1mexpj(γ+ β)+(γ 1+β 1)ImLexpj(γ+β+ 90),
где: I1m – производная модуля изображающего вектора трехфазного тока, Um – модуль изображающего вектора трехфазного напряжения, γ = ωt - угол между вращающейся осью d (система координат d-q) и неподвижной фазной осью А, β – угол между осью d и изображающим вектором тока, φ – угол между изображающим вектором тока и напряжением, expj( ) –экспоненциальная функция, аргумент которой умножается на мнимую единицу j.
Определим действительную и мнимую части векторного уравнения:
Um cosφ = ImR + L I1m ,
Um sinφ = L( γ 1 + β 1) Im .
Умножим каждое из этих равенств на 1,5Im, в результате получим выражение для мгновенной мощности трехфазной нагрузки (3), которое определяется как скалярное произведение изображающих векторов трехфазного тока, и выражение для мгновенной реактивной мощности q(t) [5]:
uaia + ubib + ucic = p(t) = 1,5 (Im)2R + 0,75Ld(Im2)/dt,
: ua(iс – ib) + ub(ia – ic) + uc(ib – ia) =√3q(t) = 1,5√3L Im2( γ 1 + β 1) (4)
:q(t) = 1,5L Im2( γ 1 + β 1) = 1,5UmImsinφ(t).
Суммарная, накопленная электромагнитная энергия в трехфазной индуктивности определяется как сумма накопленных энергий в каждой фазе:
WL(t) = 0.5L(ia2 + ib2+ ic2) = 0,75L Im2
Сравнивая два последних выражения можно заметить, что мгновенная реактивная мощность:q(t) трехфазной, симметричной нагрузки в каждый момент времени пропорциональна суммарной накопленной электромагнитной энергии, которой обладает трехфазная индуктивность, а коэффициент пропорциональности равен удвоенной угловой частоте вращения ( γ 1 + β 1) изображающего вектора трехфазного тока относительно неподвижной на плоскости фазной оси А.
Если сравнить теперь выражения для мгновенной обменной мощности и мгновенной реактивной мощности трехфазной системы, то можно записать следующее выражение:
q(t) = 2( γ 1 + β 1) ∫ q(t)обмdt = 0,75L Im2 2( γ 1 + β 1).
Мгновенную кажущуюся или мгновенную полную мощность определяем с помощью ее составляющих:
s(t) = 1,5 Um(t) Im(t).
После окончания переходного режима, для линейной трехфазной нагрузки, можно записать:
dIm/dt =0, ( γ 1 + β 1) = ω,
p(t) = 1,5 Im2R,
q(t) = 1,5 ω L Im2,
q(t)обм = 0,
s(t) = 1,5Um Im.
В соответствии с (4), для трехфазной нагрузки, можно определять мгновенную реактивную мощность как в установившихся, так и в переходных режимах. Этой мгновенной реактивной мощности в каждый момент времени пропорциональна определенная электромагнитная энергия, накопленная в трехфазной реактивности, а коэффициент пропорциональности равен удвоенной угловой частоте вращения изображающего вектора тока относительно неподвижной фазной оси. На рис. 2 и 3 представлены осциллограммы мгновенной реактивной мощности.
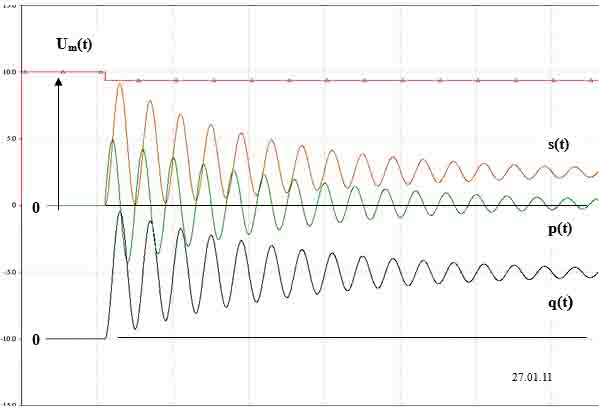
Рис. 2. Мгновенные энергетические процессы при включении трехфазной нагрузки с cos φ = 0,2.
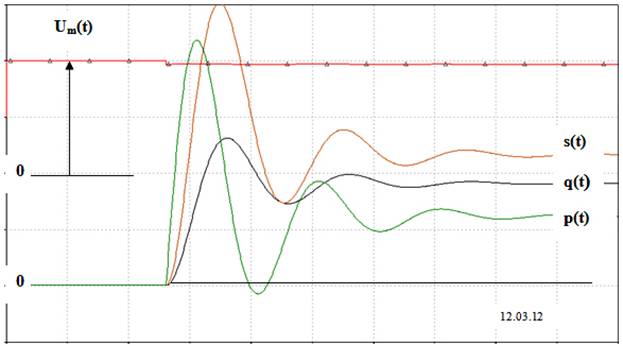
Рис. 3. Мгновенные энергетические процессы при включении трехфазной нагрузки с cos φ = 0,8.
На осциллограммах видно, что при включении нагрузки, возникает процесс обмена электромагнитной энергии между источником и потребителем, и это особенно заметно по осциллограмме мгновенной мощности, которая временами принимает отрицательные значения. В дальнейшем этот обмен прекращается, так как трехфазная реактивность заряжается, наступает установившийся режим, и мгновенная реактивная мощность своей текущей величиной определяет в каждый момент времени накопленную электромагнитную энергию в трехфазной индуктивности.
Кривые на рис. 2 и 3 можно получить и с помощью предположения, что потребитель подключен к источнику бесконечной мощности
ua = Um cos(ωt + γo),
ub = Um cos(ωt + γo–120),
uc = Um cos(ωt + γo+120).
в этом случае решение (2) представляется в виде:
ia = Um (cos(ωt + γo– φн) – cos(ωt( γo– φн) exp(-t/Ta)) /Zн,
ib = Um (cos(ωt + γo– φн –120) – cos(ωt( γo– φн–120) exp(-t/Ta)) /Zн,
ic = Um (cos(ωt + γo– φн +120) – cos(ωt( γo– φн+120) exp(-t/Ta)) /Zн,
где: γo – момент случайного включения нагрузки, φн – фаза нагрузки в установившемся режиме, Zн – модуль комплексного сопротивления нагрузки, Ta – постоянная времени нагрузки.
Теперь, с учетом сделанного допущения, мгновенную мощность и мгновенную реактивную мощность трехфазной нагрузки можно записать в виде:
p(t) = 1,5Um2(cos φн - cos(ωt + φн) exp(-t/Ta)) /Zн,
q(t) = 1,5Um2(sin φн - sin(ωt + φн) exp(-t/Ta)) /Zн.
Полученные выражения позволяют заключить, что мгновенные мощности не зависят от момента времени включения трехфазной нагрузки, а определяются только параметрами подключаемой нагрузки.
Из теории синхронной машины в осях d-q известно выражение для мгновенной мощности:
p(t) = 1,5 (udid + uqiq),
где: ud, uq, id, iq – проекции изображающих векторов напряжения и тока.
Мгновенную реактивную мощность также можно выразить через проекции изображающих векторов тока и напряжения на оси d-q, для этого необходимо использовать следующие, известные в теории синхронной машины в осях d-q соотношения:
ua = ud cosωt - uq sinωt,
ub = ud cos(ωt –120)- uq sin(ωt –120),
uc = ud cos(ωt +120) - uq sin(ωt +120),
ia = id cosωt - iq sinωt,
ib = id cos(ωt –120)- iq sin(ωt –120),
ic = id cos(ωt +120) - iq sin(ωt +120).
ua = ud cosωt - uq sinωt,
ub = ud cos(ωt –120)- uq sin(ωt –120),
uc = ud cos(ωt +120) - uq sin(ωt +120).
Подставив эти соотношения в (4) получим:
q(t) = 1,5 (uq id – ud iq)
Для однофазной и трехфазной линейных цепей, рассмотренных выше, общим является определение реактивной мощности, которая определяется как взаимное произведение модулей изображающих векторов тока и напряжения на синус угла между ними. В случае трехфазной нагрузки выражение (4) позволяет определить мгновенную реактивную мощность, или соответствующую ей мгновенную, накопленную электромагнитную энергию сети с помощью мгновенных фазных токов и напряжений. Можно предположить, что (4) справедливо и для случая нелинейных цепей.
Также (4) позволяет сделать вывод о существовании баланса мгновенных мощностей, как в узловых точках, так и по всей цепи в целом. Баланс мгновенной реактивной мощности является условием существования реактивной мощности, по Н.А.Мельникову [6] и по (4) он сохраняется в случае нелинейной нагрузки.
Рассмотрим случай включения трехфазного выпрямителя на мощную сеть, c линиями связи, имеющими нулевые сопротивления. На рис. 4 представлены осциллограммы мгновенных энергетических величин, таких как:
cosφ – мгновенный коэффициент мощности или косинус мгновенного угла между изображающими векторами трехфазного тока и напряжения, определяется по соотношению мгновенной трехфазной мощности p(t) к мгновенной кажущейся мощности s(t) [1,3.4 ];
sinφ – синус мгновенного угла между изображающими векторами трехфазного тока и напряжения, определяется по соотношению мгновенной реактивной мощности q(t) к мгновенной кажущейся мощности s(t) [5].
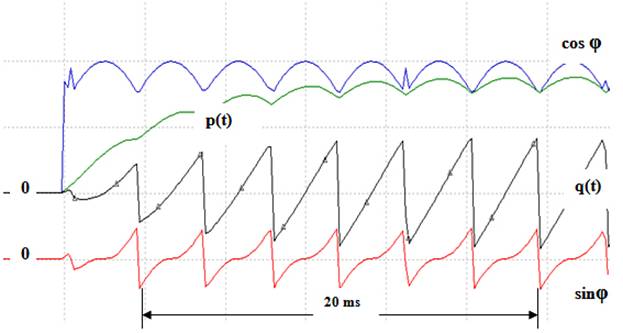
Рис. 4. Мгновенные энергетические процессы при включении трехфазного неуправляемого выпрямителя на мощную сеть.
Осциллограмма мгновенной реактивной мощности имеет «пилообразный характер» и симметрична относительно нуля. Этой реактивной мощности в каждый момент времени пропорциональна электромагнитная энергия, которую генерирует трехфазный выпрямитель в сеть, на интервалах, когда q(t) < 0, и запасает, когда q(t) > 0, при этом коэффициент пропорциональности равен удвоенной мгновенной частоте вращения изображающего вектора трехфазного тока относительно неподвижной оси А, а в установившемся режиме равен удвоенной угловой частоте основной гармоники. Необходимо заметить, что в данном случае, определение средне интегральных показателей приведет к тому, что эти показатели ∫q(t)dt/T, ∫sinφdt/T будут равны нулю, а ∫ cos φdt/T не будет равен единице.
Если по осциллограмме мгновенного cos φ можно судить об эффективности передачи электромагнитной энергии от источника к потребителю [1, 5], то по осциллограмме мгновенного sin φ можно определять интервалы времени, когда изображающий вектор трехфазного тока забегает вперед, относительно вектора напряжения, q(t) < 0, при этом потребитель приобретает»емкостной» характер, в противоположном случае, когда q(t) > 0, потребитель приобретает «индуктивный» характер.
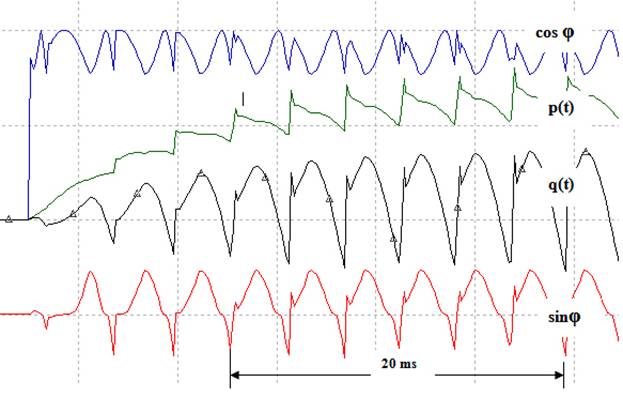
Рис. 5. Мгновенные энергетические процессы при включении трехфазного неуправляемого выпрямителя на реальную сеть.
На следующем рис. 5 показаны те же осциллограммы, но в случае включения нелинейной нагрузки в реальную сеть. Необходимо отметить, что запись, упомянутых выше энергетических параметров, производилось в точках подключения нелинейной нагрузки к питающему кабелю.
На этой осциллограмме сигнал мгновенной реактивной мощности уже несимметричен относительно нуля, как и несимметричен сигнал синуса мгновенного угла между изображающими векторами тока и напряжения.
В линейных трехфазных цепях понятие накопленной электромагнитной энергии напрямую связывают с наличием в этих цепях индуктивных или емкостных элементов. Поэтому, в силу этого привычного подхода, трудно принять, что естественная коммутация диодов, может быть причиной «емкостного» или «индуктивного» характера нелинейной нагрузки, вследствие опережающего или отстающего изображающего вектора трехфазного тока относительно изображающего вектора напряжения.
Нелинейный потребитель, на интервалах времени, когда q(t) > 0 обладает запасенной электромагнитной энергией, так как изображающий вектор тока отстает от изображающего вектора напряжения и генерирует ее, когда q(t) < 0, вследствие опережения изображающего вектора трехфазного тока относительно изображающего вектора напряжения, или можно сказать, что пульсирующий характер мгновенной реактивной мощности оказывает негативное влияние на качество электрической энергии в точке подключения нелинейной нагрузки вследствие пульсирующего потребления и последующего генерирования электромагнитной энергии нелинейным потребителем.
Итак, для линейной однофазной, линейной трехфазной, нелинейной трехфазной нагрузки, общим критерием для определения запасенной или генерируемой электромагнитной энергией является мгновенное положение изображающего вектора тока относительно изображающего вектора напряжения. В линейных цепях накопители электромагнитной энергии, если можно так сказать, оказывают «статическое» воздействие на положение изображающего вектора тока, а нелинейная трехфазная цепь оказывает «динамическое» воздействие. Вследствие этого, угол между изображающими векторами тока и напряжения не остается постоянным, а меняется с каждым моментом времени.
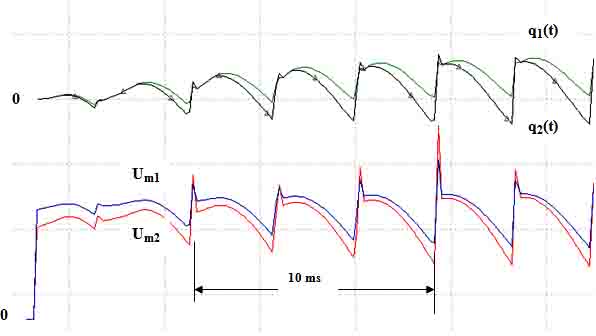
Рис. 6. Осциллограммы мгновенной реактивной мощности и модуля изображающего вектора трехфазного напряжения в точке подключения нелинейной нагрузки к питающему кабелю (2) и в точке подключения питающего кабеля к распределительному щиту (1).
На Рис..6 показаны осциллограммы в различных точках подключения. Очевидно, что формы кривых мгновенной реактивной мощности и модуля изображающего вектора очень похожи друг на друга. С удалением от нелинейной нагрузки, в точке подключения питающего кабеля к распределительному щиту, пульсация обоих кривых становится меньше, уменьшается коэффициент искажения кривой напряжения. Так как стабильность модуля изображающего вектора напряжения определяет качественное трехфазное напряжение и учитывая зависимость модуля напряжения от амплитуды размаха мгновенной реактивной мощности, то можно утверждать, о влиянии амплитуды размаха мгновенной реактивной мощности на качество трехфазного напряжения. Увеличение амплитуды размаха однозначно сказывается на ухудшении качества трехфазного напряжения.
Предлагаемое понятие мгновенной реактивной мощности трехфазного линейного или нелинейного потребителя в каждый момент времени позволяет определить мгновенную накопленную в сети или генерируемую сетью электромагнитную энергию, с точностью равной мгновенной угловой скорости вращения изображающего вектор трехфазного тока относительно неподвижной фазной оси.
Переменная составляющая мгновенной реактивной мощности однозначно влияет на качество трехфазного напряжения, поэтому целесообразно использовать сигнал мгновенной реактивной мощности в устройствах, улучшающих качество напряжения, при наличии в сети нелинейных потребителей.
Литература
1. Бондаренко А.Е. Регулирование судовых генераторных агрегатов по мгновенным значениям параметров режимов. Дисс. на соискание ученой степени к.т.н. 186 стр., СПбГМТУ, Санкт-Петербург 1992г.
2. ГОСТ 19880-74. Электротехника. Основные понятия. Термины и определения. М.: Издательство стандартов, 1984, 32с.
3. Бондаренко А.Е., Вилесов Д.В.Обобщенные мгновенные значения параметров состояния трехфазных систем. Тезисы докладов 5-ой НТК «ЭМС технических средств», Санкт-Петербург, 1998, стр. 20,.
4. Бондаренко А.Е., Вилесов Д.В.Электромагнитные параметры состояния судовых трехфазных сетей. Сборник научных докладов. Международный симпозиум по ЭМС, часть 3, Санкт-Петербург, СпбГЭИ, 1993, стр. 602-604, ,.
5. Бондаренко А.Е., Вилесов Д.В. Мгновенная активная, реактивная, полная мощность, эффективность энергопотребления в трехфазных сетях. Журнал научных публикаций аспирантов и докторантов. N10(64), октябрь 2011, стр. 94-98, Курск.
6. Мельников Н.А. Реактивная мощность в электрических сетях. М.: Энергия, 1975, 128с.
Поступила в редакцию 13.11.2013 г.