Структурные площадные реконструкции в задаче опережающего прогноза при минимуме априорной информации
Мовчан Игорь Борисович,
кандидат геолого-минералогических наук, доцент Национального минерально-сырьевого университета «Горный», г. Санкт-Петербург.
Под опережающим прогнозом понимаем определение позиции и/или геометрии областей, перспективных на детерминированный рудный или нерудный полезный компонент, а также параметрических и структурных маркеров указанных областей, на основании которых возможно планирование детализационных полевых работ. Минимум априорной информации в наших проектах означает либо географическую привязку участка и общую геологическую информацию о структурно-тектонической позиции полигона работ, либо эти данные могут дополнительно включать позицию эталонных рудных или нерудных объектов. При таких условиях исполнитель обращается к данным свободного доступа, в общем случае представленным аналоговой топоосновой в бумажной или растровой форме.
Решение задачи опирается на алгоритм интерактивной оцифровки топоосновы: карты изолиний скалярного поля абсолютных высот рельефа земной поверхности (в дальнейшем – скалярного поля), привязанной к системе географических реперов. Оцифровка в нашем случае предусматривает автоматизированное прослеживание выделенных изолиний и локализацию особых точек в структуре скалярного поля:
1) перевод топоосновы в растровый формат с определением степени контрастности между конкретной изолинией и окружающим фоном;
2) выбор способа оцифровка изолинии: если она замкнутая, то задаем начальную точку оцифровки с присваиванием ей детерминированного значения скалярного поля, а если разомкнутая, то – локализуем начальную и конечную точки оцифровки;
3) текущий шаг оцифровки определяется степенью дифференцированностью изолинии: при выположенном ее характере он принимается равным 1 см в масштабе карты, а при наличии сложных изгибов – расстоянием от одной точки перегиба изолинии до другой;
4) в начальной точке оцифровки с применением матрицы поворота организуется вращение отрезка длиной не более 1 см в масштабе карты;
5) для каждой позиции отрезка в диапазоне от 00 до 1800 вдоль его линии выполняется отбор значений поля оптической плотности изображения карты изолиний с его пересчетом в параметр пространственной изменчивости;
6) по завершению вращения отрезка строим график дисперсионного функционала с угловым аргументом и выявляем глобальный минимум этого функционала, отвечающий оптимальной ориентации отрезка – вдоль касательной к изолинии;
7) для подобранной ориентации отрезка выполняем анализ отобранных значений поля оптической плотности: его монотонный характер (наличие не более одного экстремума) указывает на слабую дифференцированность изолинии, немонотонный характер – на сильную ее дифференцированность;
8) выбирается оптимальный шаг оцифровки: в случае слабой дифференцированности он равен исходной длине отрезка (1 см в масштабе карты), в противном случае он равен расстоянию от точки вращения отрезка до первого экстремума поля оптической плотности;
9) точке оцифровке присваивается детерминированное на первом шаге алгоритма значение изолинии с организацией вращения условного вектора относительно новой точки;
10) процесс продолжается вплоть до достижения начальной точки оцифровки в случае замкнутой изолинии, либо до достижения установленной пользователем конечной точки оцифровки в случае разомкнутого характера изолинии.
В отличие от реализации элементарной функции дигитайзера предложенный алгоритм ускоряет операцию оцифровки и сокращает число промежуточных операций, в частности, количество текущих разбиений итогового файла оцифровки. Максимально полная коррелируемость аналоговой карты изолиний и ее цифровой модели требует дополнительных процедур: оцифровки точек экстремума как центров кривизны замкнутых изолиний; локализации узловых точек, определяемых как точки пресечения двух одноименных изолиний; оцифровки изолиний за пределами исследуемого полигона (в отсутствие данных карта либо экстраполируется на основе аналитического тренда, либо прорисовывается вручную). Итоговый цифровой массив применяется для интерполяции несколькими методами (минимальной кривизны, модифицированным способом Шепарда, радиальной базисной функции) с выбором цифровой модели, обладающей наименьшим разбросом значений скалярного поля. Следующим шагом идет структурная обработка итоговой цифровой модели с выделением прогнозных маркеров.
Основным элементом обработки выступает подсветка условной поверхности скалярного поля с применением образа гомоцентрического источника и предположения о Ламбертовом рассеянии отраженного света элементом этой условной поверхности [1]. Операция выполняет контрастирование протяженных структурных форм, проявленных в значениях скалярного поля и ориентированных субортогонально направлению подсветки. Повышение контрастности и степени детальности итогового морфоструктурного образа достигается на основе системы дифференциальных операторов, численно реализуемых в предметной плоскости в рамках операции свертки [2], например, оператора Собела. На итоговый полутоновой образ можно накладывать результат кластерного пересчета скалярного поля, включающего построение семейства дискриминантных функций, разбивающих множество значений этого поля на конечное число групп, каждое из которых отвечает гомогенным геологическим объектам. Это представляется как выделение в структуре эмпирически накопленной гистограммы распределения значений скалярного поля семейства независимых мод [3]. Окончательно применяем авторский алгоритм линеаментно-спектрального анализа [4]:
- поиск по площади исследуемого полигона точек экстремума и точек перегиба скалярного поля с организацией вращения относительно каждой из этих точек условного вектора;
- отбор вдоль линии каждого вектора значений скалярного поля и модуля вектора его горизонтального градиента с расчетом углового функционала изменчивости;
- определение оптимальной ориентации каждого из вращающихся векторов и объединение семейства этих векторов в конечный набор линейных или дуговых региональных структурных элементов на основании локализации глобального минимума углового функционала изменчивости.
Итог такого пересчета имеет форму генерализованной линеаментно-структурной схемы (рис. 1), подлежащей классификации по таким критериям как степень контрастности, протяженности, пространственной коррелируемости с явными особенностями скалярного поля (например, зоной перехода от повышенных к пониженным значениям). Наибольший интерес здесь представляют области пересечения максимального числа линеаментных структур, пространственно коррелирующиеся с циркоидными образованиями нескольких порядков: опыт показывает, что их можно интерпретировать как области наибольшей проницаемости земной коры и связывать с ними рудный прогноз при наличии пространственной регулярности в семействе подобных областей [4].
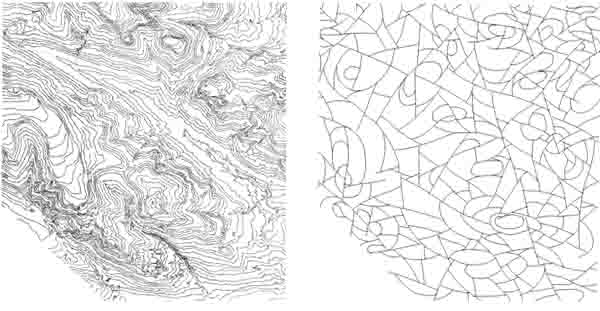
а) б)
Рис. 1. Формирование базы данных по первичным структурным маркерам полигона: а) результат оцифровки аналоговой топоосновы; б) линеаментно-структурная схема.
Литература
1. Dods S.D., Teskey D.J., Hood P.J. The new series of 1:1 000 000-scale magnetic anomaly maps of Geological Survey of Canada: compilation techniques and interpretation // The utility of regional gravity and magnetic anomaly maps. – Tulsa, Oklahoma. – 1985. – p.69-87.
2. Прэтт У. Цифровая обработка изображений // М., Мир. – т.2. – 1982. – с.508-514.
3. Дэвис Дж. Статистика и анализ геологических данных // М., Мир. – 1977. – с.472-486.
4. Мовчан И.Б., Петров О.В., Яковлева А.А., Кирсанов А.А. Способ автоматизированного структурного дешифрирования космоснимков // Региональная геология и металлогения, №23. – СПб, ВСЕГЕИ. – 2005. – с.45-50.
Поступила а редакцию 16.01.2013 г.