Общий методологический подход при исследовании региональных геотрансектов России. Часть 1

 

Мовчан Игорь Борисович,

кандидат геолого-минералогических наук, доцент Национального минерально-сырьевого университета «Горный», г. Санкт-Петербург.

 

Основу всякого моделирования составляет информационная база данных, описывающая в нашем случае полосовую зону Мурманск-Кызыл:

·                    материалы геологического картирования;

·                    данные многоволнового глубинного сейсмического зондирования (ГСЗ);

·                    данные гравиметрии;

·                    геотермические измерения;

·                    описания глубоких и сверхглубоких скважин;

·                    петрофизические данные;

·                    аэро-космические снимки и результаты линеаментного анализа топографических карт.

Собственно методология обработки этой информации была составлена из двух технологических линий, ориентированных на две принципиальные задачи:

-                     изучение латерального распределения структурно-петрофизических неоднородностей Земной коры на разных глубинных уровнях;

-                     исследование вертикального и объемного распределения преобладающих структурно-петрофизических неоднородностей литосферы.

Ключевую роль в решении первой задачи играют процедуры фильтрации, последовательной редукции гравитационного и магнитного полей и коммутация их спектрально коррелируемых составляющих. Результаты интерпретации сейсмических и геотермических материалов принимаются как вспомогательные.

В рамках второй технологической линии сейсмические и геотермические данные рассматривались как определяющие. В варианте ГСЗ, развиваемым Центром ГЕОН, упругие волны создавались взрывными источниками, в том числе ядерными. Упругие P, S и P-S волны записывались на трехкомпонентных регистрирующих системах. Существующая методика позволяет судить об изменении скоростей волн в пределах Земной коры и верхней мантии. Оценка этих скоростей выполняется для зон мощностью от 4 до 15 км и 40-100 км протяженностью. Ошибка в оценке глубин сейсмических границ не превышала 5%. Сейсмические разрезы исходно представлялись в форме блоков (зон), ограниченных системой субвертикальных, субгоризонтальных и менее часто – наклонными поверхностями раздела (рис.1).

 

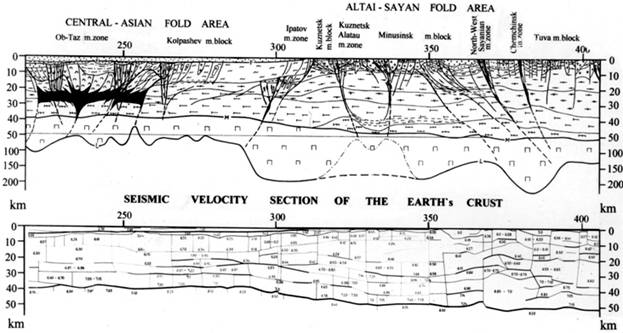
Рис. 1. Сопоставление глубинных тектонических реконструкций (верхний эскиз) со схематическим представлением сейсмического скоростного разреза (по Егорову А.С., 1997).

 

Статистический алгоритм анализа ГСЗ-разреза основывается на суммировании числа элементарных P, S и P-S волновых площадок, выполняемом в окне, скользящем по плоскости вертикального разреза. Сами площадки являются центрами малых структурных элементов, отражающих, преломляющих и инвертирующих упругие волны. Указанная процедура дифференцирует вертикальный разрез по степени его гетерогенности, что часто позволяет выделять полого погружающиеся тектонические структуры: границы палеоплит, микроплиты, тектонические покровы, надвиги и т.д.. В общем случае палеоплиты и микроплиты характеризуются тонкой расслоенностью Земной коры с выделением верхне- средне- и нижнекоровых мегаслоев согласно их скоростным параметрам. Внутриблоковые мегазоны, сформированные в окружении, подвергнутом напряжениям сжатия, растяжения и смещенные по простиранию, характеризуются сейсмически нестратифицированной Земной корой.

Алгоритмы глубинного геотермического моделирования обеспечивают оценку изменения мощности литосферы (рис. 2).

 

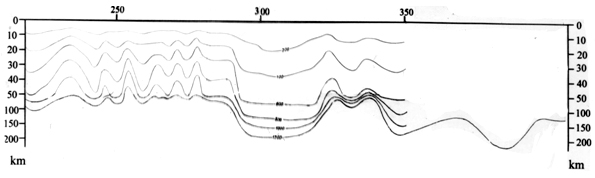
Рис. 2. Геотермальный разрез литосферы вдоль геотрансекта, представленного на рис.1 (по Егорову А.С., 1997).

 

Для моделирования вертикального разреза рассматривался широкий класс процедур решения прямой и обратной задач в гравиметрии и магнитометрии с оценкой интегральных плотности и намагниченности аномалеобразующих источников верхней и отчасти средней коры (стадия монометодной интерпретации). Кроме того, обработка грави-магнитных полей использовалась для подтверждения окончательных геолого-геофизических разрезов литосферы; в качестве формального критерия рассматривалось совпадение наблюденного и вычисленного геофизического поля.

До сих пор основными объектами нашего геолого-геофизического моделирования были: массивы (мегаблоки) древней континентальной коры и межблоковые мегазоны, соответствующие протяженным, сжатым и подвергшихся интенсивным сдвигам областям.

Вертикальный разрез древней континентальной «нормально стратифицированной» литосферы включает (сверху вниз) мегаслои с характерной скоростью V_p и плотностью :

·                    осадочно-вулканический мегаслой (V_p = 2.5 – 4.5 км/с;  гр/см³);

·                    верхняя кора (V_p = 6.0 – 6.4 км/с;  гр/см³);

·                    средняя кора (V_p = 6.5 – 6.8 км/с;  гр/см³);

·                    нижняя кора (V_p = 6.9 – 7.2 км/с;  гр/см³);

·                    верхнемантийный мегаслой (V_p > 7.8 км/с; >3.25 гр/см³).

Межблоковые мегазоны характеризуются сейсмически нестратифицированной корой и их внутренняя структура, и петрологический состав оцениваются по результатам грави-магнитометрических моделирований.

В нашей работе мы делаем особый акцент на такие аномальные геофизические объекты как:

·                    область нижней коры с повышенной скоростью упругих волн (сверх 7.2 км/с);

·                    верхнемантийная область с аномально низкими скоростями (менее 7.8 км/с);

·                    коровые и верхнемантийные субгоризонтальные низкоскоростные зоны.

Комплексы пород классифицируются согласно возрасту и геодинамическому окружению.

Для описания структуры грави-магнитных полей, дающих площадной образ рассматриваемой полосовой зоны, применялись три процедуры:

1)                 полутоновое представление условных поверхностей, создаваемых множеством амплитудных значений исходных геофизических полей, измеренных в пределах полосовой зоны геотрансекта [1];

2)                 полутоновое представление грави-магнитных полей после их трансформации оператором Собела [2];

3)                 конечно-элементное представление отмеченных выше поверхностей грави-магнитных полей [3].

Основу первой процедуры составляет численное моделирование освещения поверхности с использованием уравнением фотометрии. В частности, овещенность поверхности:

,                                                                                                      (1)

где  - интенсивность источника света,  - угол падения,  - расстояние от источника до данной точки освещаемой поверхности. При этом

,                                                                                          (2)

где , , Z – амплитудные значения рассматриваемого геофизического поля,  - угол между направлением освещения элементарной площадки и проекцией этого направления на горизонтальную плоскость,  - угол между этой проекцией и условным направлением на север. Поворот источника света относительно фиксированных на площади измерений геофизического поля позволяет разделить наложенные геологические структуры разного простирания без искажения редуцированной структуры этого поля.

Оператор Собела [2] подчеркивает области смены структуры рисунка, оконтуривая их четкими локальными по ширине зонами высокого горизонтального градиента. При дискретном задании сигнала любой из этих операторов принимает матричный вид:

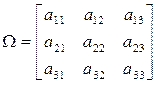,                                                                                         (3)

что в компьютере задается как скользящее по выборке окно 3х3. Каждый из членов матрицы заполняется соответствующим значением поля и затем строится разностная схема. Окончательный результат присваивается центру окна, т.е. элементу . В частности для оператора Собела:

,                                                   (4)

,                                                   (5)

.                                                                                                   (6)

Все итоговые полутоновые изображения приводятся к единому масштабу.

Алгоритмическая схема конечноэлементного разбиения поверхности геофизических полей включает:

·                    расчет двумерной автокорреляционной функции с использованием интеграла свертки;

·                    выделение точек экстремума исходного поля и его горизонтального градиента;

·                    организация вращения конечного элемента вокруг каждой из этих точек;

·                    сплайн-интерполяция значений геофизического поля, выполняемая вдоль каждого положения конечного элемента [4];

·                    расчет дисперсии геофизического поля по результатам сплайн-интерполяции;

·                    определение оптимального простирания конечного элемента на основе критерия минимума дисперсии геофизического поля.

При решении обратной задачи мы отталкивались от предположения, что вся информация о распределении источников по глубине сосредоточена в спектре магнитного и гравитационного полей. При этом подразумевался статистический характер распределения амплитудно-частотных характеристик этих полей вдоль избранных профилей. Окончательно, мы приходим к оценке пространственной стационарности геофизического двумерного сигнала на основе такого интегрального параметра как радиус автокорреляции:

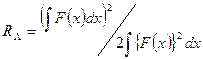.                                                                              (8)

В общем случае предельная глубина залегания аномалеобразующего источника:

.                                                                                                         (9)

На практике рекомендуется жестко детерминировать форму источника. Скажем, для бесконечной материальной линии , а для сферы  [5].

 

Литература

 

1.                  Dods, J.D, Teskey, P.J.: The new series of 1:1000000-scale magnetic anomaly maps of the Geological Survey of Canada. Compilation technique and interpretation. The utility of regional gravity and magnetic anomaly maps. USA, Tulsa, Oklahoma, 1985, p.p.69-87.

2.                  У. Прэтт: Цифровая обработка изображений. М., т.2, с.500-517.

3.                  Л. Сегерлинд: Применение метода конечных элементов. М., 1979, с. 17-65.

4.                  А.Е. Мудров: Численные методы для ПЭВМ на языках БЕЙСИК, ФОРТРАН и ПАСКАЛЬ. Томск, 1992, с.96-105.

5.                  С.А. Серкеров: Спектральный анализ в гравиразведке и магниторазведке. М., 1991, с.198-211.

 

Поступила в редакцию 19.03.2013 г.