Параметризация регулятора межконтуров стабилизации диаметра изоляции и погонной емкости кабеля связи с парной скруткой

 

Смородинов Дмитрий Александрович,

аспирант Самарского государственного технического университета.

 

Изготовление кабелей связи подвержено влиянию случайных возмущающих воздействий. Поэтому, несмотря на наличие встроенных локальных систем автоматической стабилизации (САС), большинство технологических режимных параметров и контролируемых «на проход» параметров кабельного изделия имеют непостоянные по длине кабеля значения и являются случайными функциями координаты длины кабеля x. Линии с переменными по длине параметрами принято называть нерегулярными. Как правило, нерегулярность параметров кабеля по длине невелика и составляет единицы, а чаще десятые и сотые доли процента от номинальных значений. Следовательно, кабели являются слабонерегулярными линиями. Тем не менее, слабое непостоянство размеров и свойств кабеля по длине решительным образом влияет на характер распространения электромагнитных волн и параметры кабеля, среди которых необходимо выделить обобщенный параметр, количественно характеризующий уровень нерегулярности кабеля и, соответственно, его качество [1].

Количество организуемых по кабелю каналов связи и длина усилительного участка (или тракта) определяются первичными и вторичными параметрами передачи. В связи с тем, что передача сигнала в кабелях связи осуществляется по многим двухпроводным цепям, расположенным в непосредственной близости друг от друга, наблюдается взаимное влияние между цепями, приводящее к появлению переходных шумов и разговоров, которые характеризуются с помощью первичных и вторичных параметров влияния [2].

Достижение минимального уровня нерегулярности кабеля возможно только при оптимальном управлении его параметрами, формируемыми в ходе технологического процесса. При изготовлении низкочастотных кабелей хороший результат дает оптимизация по типовым критериям оптимизации – максимуму быстродействия или минимуму дисперсии ошибки. Лучшие результаты дает использование регуляторов, робастных к скорости технологического процесса и межконтурных терминальных регуляторов.

Для слабонерегулярной кабельной линии телеграфные уравнения, описывающие распространение волн вдоль линии, могут быть сведены к уравнению Риккати относительно входного коэффициента отражения в произвольном сечении кабеля с координатой x. Решение этого уравнения имеет вид [2]:

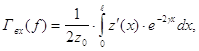,                                                                               (1)

где - частота передаваемого сигнала, - номинальное значение волнового сопротивления, - производная функции волнового сопротивления по длине кабеля , -длина кабеля, -коэффициент распространения электромагнитной волны.

,                                                                                                                (2)

где - коэффициент затухания,  - коэффициент фазы;

                                                                                                               (3)

                                                                                                                    (4)

где  - частота, L – индуктивность линии на единицу длины, С – емкость линии на единицу длины;

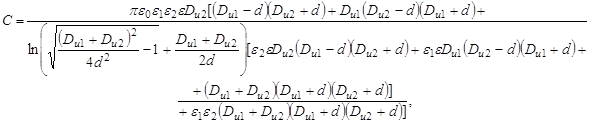 (5)

где  - диаметр медной жилы,  - соответствующие диаметры изоляций жил,  - соответствующие диэлектрические проницаемости изоляций жил кабеля,  - диэлектрическая проницаемость среды между изолированными жилами кабеля и внешним защитным покрытием или экраном,  - электрическая постоянная (рис. 1) [3].

 

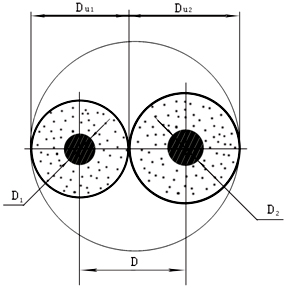
Рис. 1. Сечение LAN-кабеля.

 

Индуктивность линии на единицу длины равна для витой пары LAN-кабеля [4]:

                                                                                               (6)

С учетом (4)-(6), волновое сопротивление может рассчитываться по формуле:

                                                                                                       (7)

где  - эквивалентная диэлектрическая проницаемость изоляции витой пары LAN-кабеля [3]:

(8)

 

Выражения (7) позволяет выразить нерегулярность волнового сопротивления LAN-кабеля через вариации его параметров , формируемых в процессе изготовления [5]:

,                                                                      (11)

где

                                                             (12)

 - чувствительность волнового сопротивления к малым вариациям i-того параметра кабеля.

Зависимость волнового сопротивления  может быть достаточно точно представлена в виде:

                                                                        (13)

где  и  - чувствительности волнового сопротивления к вариациям диаметра и емкости, определяемые как частные производные от соответствующей функции волнового сопротивления. Выражение (13) позволяет определить структуру многоконтурной системы стабилизации диаметра и емкости, позволяющую минимизировать вариации волнового сопротивления ∆z(x).

Известны временные подходы к оптимизации управления, где использован «плавный переход», минимизирующий коэффициент отражения в произвольном сечении кабеля (1). Целесообразно минимизировать среднее значение модуля входного коэффициента отражения в рабочем диапазоне частот :

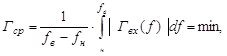                                                                         (14)

                                                                      (15)

где  - границы рабочего диапазона частот.

В известном «плавном переходе» от волнового сопротивления  до , функция  линейная (рис. 2), т. е.

                                                                                                             (16)

 

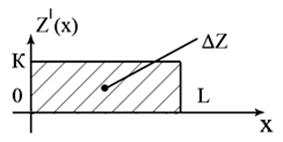
Рис. 2. График производной функции .

 

Потому для минимизации (14), (15) с учетом (1) на конечном отрезке  с учетом частотной зависимости коэффициента затухания α, оптимальная будет гармоническая форма нерегулярности с той же площадью  (рис. 3).

 

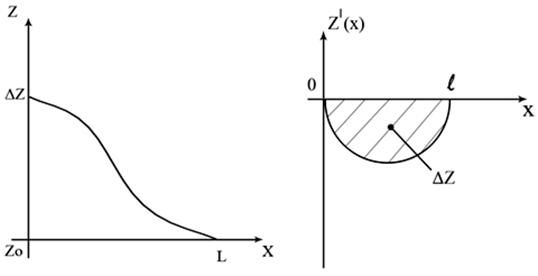
Рис. 3. График функции и её производной при гармонической форме нерегулярности.

 

При такой форме нерегулярности максимальное значение модуля входного коэффициента отражения (15) на резонансной частоте примет вид:

                                                                 (17)

Обозначим величину коэффициента отражения на произвольной фиксированной частоте f через  и перепишем выражение (1) в следующем виде:

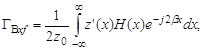                                                                              (18)

где

.                                                                                     (19)

Величина , входящая в выражение (18), определяет угловую пространственную частоту гармоники функции , взаимодействующей с гармоническим сигналом частоты[5]:

,                                                                            (20)

где v – фазовая скорость; l_в – длина волны взаимодействующей гармоники; g – пространственная частота взаимодействующей гармоники:

.                                                                                                                    (21)

С учетом (20) выражение (18) можно представить в виде:

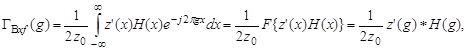             (22)

т.е. величина входного коэффициента отражения определяется преобразованием Фурье от произведения функции  и  или же сверткой их спектров Фурье.

При построении спектра линейной нерегулярности (рис. 4), отклонение функции стремиться к нулю при , и оптимизировать нужно путем минимизации модуля , именно когда исследуется коэффициент отражения в произвольном сечении кабеля.

 

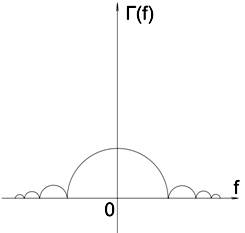
Рис. 4. Спектр с линейной формой нерегулярности.

 

Гармоническая форма  с пространственной частотой, большей, чем верхняя граница g, даст пик рефлектограммы  на резонансной частоте , выше, чем , т.е. вне спектра рабочих частот (рис. 5).

 

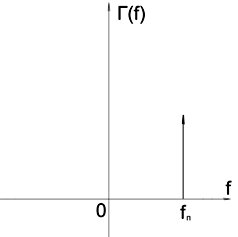
Рис. 5. Спектр с гармонической формой нерегулярности.

 

Данный вывод позволяет организовать оптимальное управление технологическим процессам производства LAN-кабеля, при выборе его параметров согласно требованиям заказчика, а в частности, рабочего диапазона частот.

 

Литература

 

1.                  Гроднев И.И., Шварцман В.О. Теория направляющих систем связи. М.: Связь, 1978. 296 с.

2.                  Гальперович Д.Я., Павлов А.А., Хренков Н.Н. Радиочастотные кабели. М.: Энергоатомиздат, 1990. 256 с.

3.                  Чостковский Б.К., Смородинов Д. А. Математическая модель витой пары радиочастотного кабеля объекта управления // Вестн. Самар. гос. техн. у-та. 2008. Вып. 1. с. 113-119.

4.                  Глебович Г. В., Ковалев И. П. Широкополосные линии передачи импульсных сигналов. М., «Сов. Радио», 1973, 224 с.

5.                  Чостковский Б. К. Математическая модель формирования обобщенны параметров качества нерегулярных кабелей связи в стахастической постановке // Вестн. Самар. гос. техн. у-та. 2006. Вып. 42. с. 147-161.

 

Поступила в редакцию 27.03.2013 г.